Слайд 2Исторический экскурс
3 сентября декабря – день комп. графики (3December)
Слайд 3Исторический экскурс
1950-е годы: от текстовых изображений к графической консоли

Слайд 41950-е годы
1950, Бенджамин Лапоски, рисунки на осциллографе

Слайд 51950-е годы
1952, Александр Дуглас, игра ОХО для компьютера EDSAC

Слайд 61950-е годы
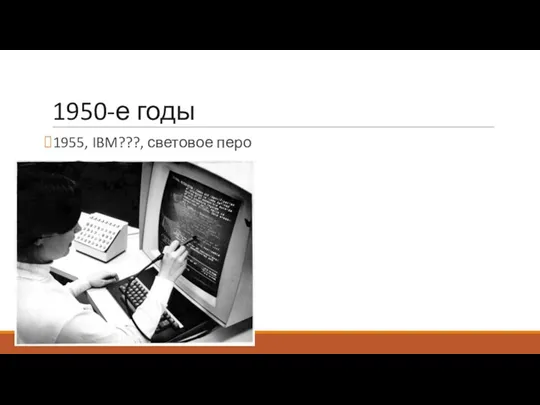
1955, IBM???, световое перо
Слайд 71950-е годы
1957, Расселл Кёрш, барабанный сканер для компьютера SEAC, первая в мире цифровая
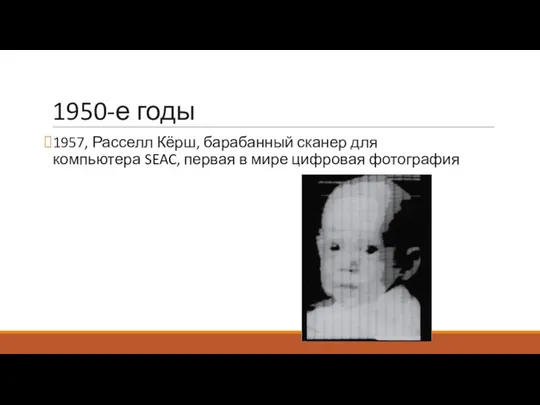
фотография
Слайд 81950-е годы
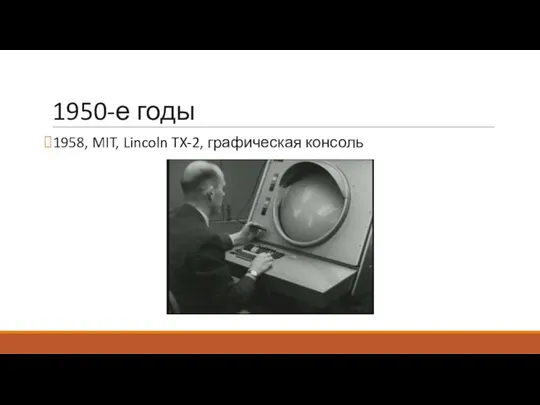
1958, MIT, Lincoln TX-2, графическая консоль
Слайд 91950-е годы
1958, Джон Уитни, предиктор Керрисона, заставка к фильму Хичкока «Головокружение»

Слайд 101960-е годы: от "Альбома" к мультипликации
1960, Уильям Феттер, Boeing Aircraft, термин «компьютерная

графика»
Слайд 111960-е годы
1962, Стив Рассел, Spacewar! для компьютера DEC PDP-1

Слайд 121960-е годы
1963, Айван Сазерленд, Sketchpad для TX-2

Слайд 131960-е годы
1963, Кен Ноултон, BeFlix – первый язык КГ
1965-1971, Стэн Вандербик, Poem

Field
1967, университет Юты, НИИ КГ
1968, Evans&Sutherland
Эдвин Кэтмелл, Disney Pixar
Джон Уорнок, Adobe Systems, PostScript
Джеймс Кларк, Silicon Graphics, Netscape
1968, Николай Константинов, «Кошечка»
Слайд 14Алгебраическое изображение точек

Слайд 15Матричные операции. Определения.
Матрица
Порядок матрицы
Главная диагональ
Нулевая матрица
Единичная матрица

Слайд 17Умножение матриц
A[k * m1], B[m2 * n], m1=m2 → A * B
![Умножение матриц A[k * m1], B[m2 * n], m1=m2 → A *](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/974704/slide-16.jpg)
= C[k * n]
Слайд 18Определитель квадратной матрицы
Aij – алгебраическое дополнение матрицы A (матрица (n-1)*(n-1), получаемая путем

вычеркивания из матрицы А элементов i-ой строки и элементов j-ого столбца)
Слайд 20Обращение квадратной матрицы
АТ = В → , А-1 — обратная к А
T

– операция транспонирования(строки – в столбцы, столбцы – в строки)
Слайд 21Обобщение сути задач КГ
Интерпретация матричного умножения как геометрического оператора является основой математических

преобразований, используемых в машинной графике.
Слайд 22Преобразование точек
a>1 – увеличение масштаба,
0а<0 – отображение по оси

у
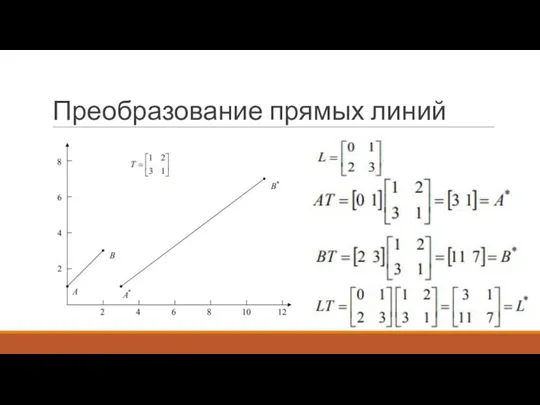
Слайд 27Преобразование параллельных линий

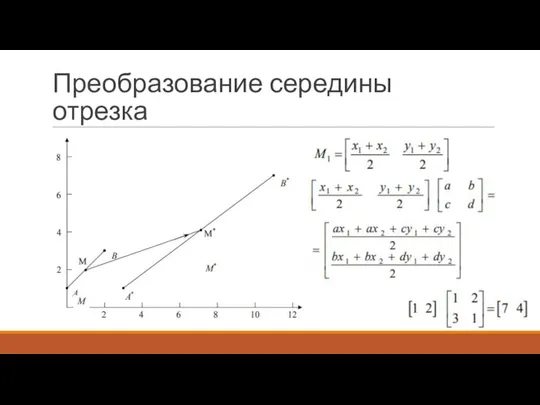
Слайд 28Преобразование пересекающихся линий

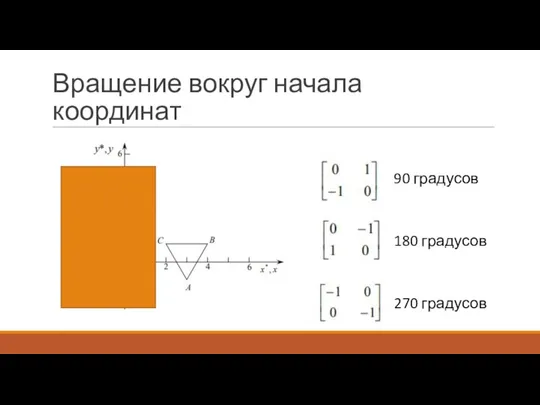
Слайд 29Вращение вокруг начала координат
90 градусов
180 градусов
270 градусов
Слайд 31Изменение масштаба
Изменение масштаба определяется значением двух членов основной диагонали матрицы.
a=d – масштабирование
a<>d

– масштабирование с искажением
Слайд 33Однородные координаты и двумерное смещение
Представление n-мерного вектора (n+1)-мерным называется однородным координатным воспроизведением;

координаты x, y, h - однородными координатами.
Слайд 34Однородные координаты и двумерное смещение
Все преобразования матрицей 2×2 (вращение, отображение, покоординатное масштабирование,

смещение) реализуются в однородных координатах с помощью матрицы:
Слайд 35Общий вид матрицы преобразования 3х3
a, b, c, d – масштабирование, сдвиг и

вращение
m, n – перенос(двумерное смещение)
p, q, s – ???
Слайд 36Полное изменение масштаба
Аналогично использованию двумерной матрицы
s>1 – уменьшение, s<1 – увеличение

Слайд 37Получение проекций
Переменная H – уравнение плоскости в трёхмерном пространстве
















![Умножение матриц A[k * m1], B[m2 * n], m1=m2 → A *](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/974704/slide-16.jpg)


















 Задача на процкеты
Задача на процкеты Параллелограмм и трапеция. Урок 6
Параллелограмм и трапеция. Урок 6 Построение сечений
Построение сечений Функции и графики
Функции и графики Степенные функции
Степенные функции Моделирование на графах
Моделирование на графах Шар. Куб. Параллелепипед
Шар. Куб. Параллелепипед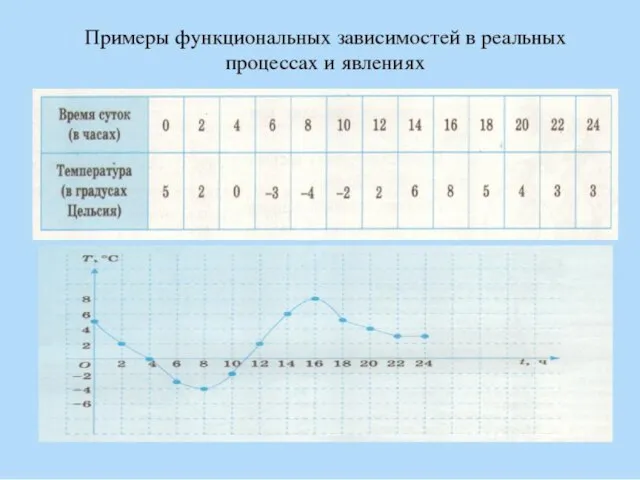 График функции. Примеры
График функции. Примеры В мире рациональных уравнений
В мире рациональных уравнений Возникновение слова “процент”. Древний Рим
Возникновение слова “процент”. Древний Рим Аксиомы планиметрии (часть 2)
Аксиомы планиметрии (часть 2) Квадратные корни
Квадратные корни Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики
Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики Делители и кратные
Делители и кратные Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Решение логических задач
Решение логических задач Решение задания 12 ЕГЭ (профиль)
Решение задания 12 ЕГЭ (профиль) Признаки параллельности двух прямых
Признаки параллельности двух прямых Золотое сечение (продолжение)
Золотое сечение (продолжение) Сфера и шар. Уравнение сферы
Сфера и шар. Уравнение сферы Математика на кухне
Математика на кухне Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление
Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление Усовершенствование навыков действий с рациональными числами
Усовершенствование навыков действий с рациональными числами Индивидуальное задание №8. Построение линии пересечения тора и конуса
Индивидуальное задание №8. Построение линии пересечения тора и конуса Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Исследование функции
Исследование функции Уравнения и неравенства с одной переменной. Урок разноуровнего обобщающего повторения
Уравнения и неравенства с одной переменной. Урок разноуровнего обобщающего повторения