Kombinatorika

ДРЕВНОСТЬ И СРЕДНИЕ ВЕКА
Комбинаторные мотивы можно заметить в символике китайской «Книги Перемен» (V век до н. э.). По мнению её авторов, всё в мире комбинируется из различных сочетаний мужского и женского начал, а также восьми стихий: земля, горы, вода, ветер, гроза, огонь, облака и небо. Историки отмечают также комбинаторные проблемы в руководствах по игре в Го и другие игры. Большой интерес математиков многих стран с древних времён неизменно вызывали магические квадраты.
Классическая задача комбинаторики: «сколько есть способов извлечь m элементов из N возможных» упоминается ещё в сутрах древней Индии (начиная примерно с IV века до н. э.). Индийские математики, видимо, первыми открыли биномиальные коэффициенты и их связь с биномом Ньютона. Во II веке до н. э. индийцы знали, что сумма всех биномиальных коэффициентов степени n равна 2n
В XII веке индийский математик Бхаскара в своём основном труде «Лилавати» подробно исследовал задачи, связанные с перестановками и сочетаниями, включая перестановки с повторениями.
В Западной Европе ряд глубоких открытий в области комбинаторики сделали два еврейских исследователя, Авраам ибн Эзра (XII век) и Леви бен Гершом (он же Герсонид, XIV век). Ибн Эзра подсчитывал число размещений с перестановками в огласовках имени Бога и обнаружил симметричность биномиальных коэффициентов, а Герсонид дал явные формулы для их подсчёта и применения в задачах вычисления числа размещений и сочетаний.
Несколько комбинаторных задач содержит «Книга абака» (Фибоначчи, XIII век). Например, он поставил задачу найти наименьшее число гирь, достаточное для взвешивания любого товара весом от 1 до 40 фунтов.
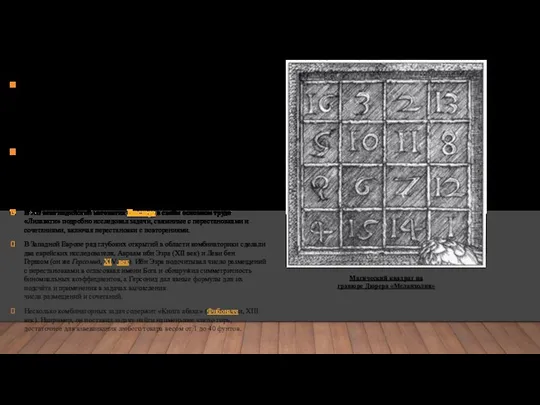
Магический квадрат на гравюре Дюрера «Меланхолия»

Комбинаторика (иногда называемая комбинаторным анализом) — раздел математики, посвящённый решению задач, связанных с выбором и расположением элементов некоторого (чаще всего конечного) множества в соответствии с заданными правилами. Каждое такое правило определяет некоторую выборку из элементов исходного множества, которая называется комбинаторной конфигурацией. Простейшими примерами комбинаторных конфигураций являются перестановки, сочетания и размещения
Типичные задачи комбинаторики:
Определить количество комбинаторных конфигураций, соответствующих заданным правилам (в частности, доказать или опровергнуть их существование).
Найти практически пригодный алгоритм их полного построения.
Определить свойства заданного класса комбинаторных конфигураций.
Комбинаторика тесно связана со многими другими областями математики - алгеброй, геометрией, теорией вероятностей, теорией чисел и другими. Она применяется в самых различных областях знаний (например, в генетике, информатике, статистике, статистической физике, лингвистике).
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

1. РАЗМЕЩЕНИЯ
Размещениями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их распоряжения.
Число размещений из n элементов по m обозначаются символом Аm/n и вычисляется формулой

2. ПЕРЕСТАНОВКИ
Перестановками из n элементов называются такие соединения из всех n элементов, которые отличаются друг от друга порядком распоряжения элементов.
Число перестановок из n элементов обознается символом Pn.
Перестановки представляют частный случай размещений из n элементов по n в каждом, т.е.
или

2.1 ПЕРЕСТАНОВКИ
Число всех перестановок из n элементов равно произведению последовательных чисел от 1 до n включительно.
Произведение 1*2*3...(n-1)*n обозначают символом n!, причем полагают
0! = 1, 1! = 1. Поэтому равенство можно переписать в виде
Используя формулу из размещения, формуле Pn можно придать вид
При решении задач часто используется равенство

3.СОЧЕТАНИЕ
Сочетаниями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга хотя одним элементом.
Число сочетаний из n элементов по m обозначается
Оно находится по формуле
Которую можно записать в виде