Комбинации многогранников и тел вращения

ШАР И МНОГОГРАННИК
Определение 1. Шар называется вписанным в многогранник, если он касается всех его граней.
Определение 2. Шар называется описанным около многогранника, если все вершины многогранника лежат на поверхности шара.
!!!ЗАПОМНИ Если шар можно вписать в параллелепипед или описать около него, то центр шара находится в точке пересечения диагоналей параллелепипеда.
Определение 3. Шар (сфера) называется вписанным в цилиндр, если он касается оснований цилиндра и всех его образующих по окружности большого круга.

ШАР И МНОГОГРАННИК
Определение 4. Шар (сфера) называется описанным около цилиндра, если окружности оснований цилиндра касаются поверхности шара (сферы).
ЗАМЕЧЕНИЕ. И в том и в другом случае ось цилиндра проходит через центр шара.
Определение 5. Шар (сфера) называется вписанным в конус, если он касается основания конуса и всех его образующих.
Определение 6. Шар (сфера) называется описанным около конуса, если окружность основания конуса и его вершина лежат на поверхности шара (на сфере).
ЗАМЕЧЕНИЕ. И в том и в другом случае ось конуса проходит через центр шара (сферы).

Правильная треугольная пирамида и сфера, шар
1. В любую правильную пирамиду можно вписать шар.
2. Шар касается основания в его центре, а боковых граней – в точках, лежащих на апофемах.

Правильная треугольная пирамида и сфера, шар
3. Центр шара, вписанного в правильную пирамиду, лежит на пересечении высоты пирамиды и биссектрисы угла, образованного апофемой и ее проекцией на основание.

Правильная треугольная пирамида и сфера, шар
1. Основание высоты правильной пирамиды совпадает с центром описанной около основания окружности.
2. Центр шара, описанного около правильной треугольной пирамиды, лежит на пересечении высоты пирамиды (или ее продолжении) и серединного перпендикуляра к ребру пирамиды, проведенного в плоскости, образованной этим ребром и высотой пирамиды.

Правильная треугольная пирамида и сфера, шар
3. Найдя центр шара, рассматриваем подобие прямоугольных треугольников.

Правильная четырехугольная пирамида и сфера, шар
1. Радиус шара, вписанного в правильную четырехугольную пирамиду, равен радиусу окружности, вписанной в равнобедренный треугольник, где боковые стороны – апофемы пирамиды, а основание – сторона основания пирамиды.

Правильная четырехугольная пирамида и сфера, шар
1. Радиус сферы, описанной около правильной четырехугольной пирамиды, равен радиусу окружности, описанной около ее диагонального сечения.
2. Диагональное сечение четырехугольной пирамиды – РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК, где основание – диагональ квадрата, а боковые стороны – боковые ребра пирамиды.

Правильная четырехугольная пирамида и сфера, шар
3. Для нахождения радиуса сферы, равного радиусу окружности, описанного около диагонального сечения можно воспользоваться следующими формулами:

1. Шар, вписанный в многогранник, касается граней всех двугранных углов этого многогранника.
2. Центр шара, вписанного в пирамиду лежит на пересечении биссекторных полуплоскостей всех ее двугранных углов.
Произвольная пирамида и сфера, шар

Произвольная пирамида и сфера, шар

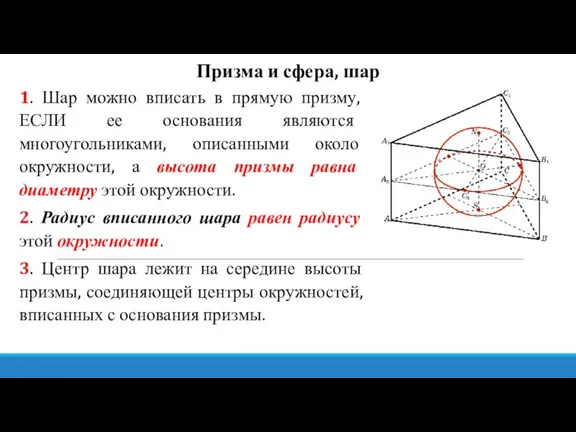
Призма и сфера, шар
1. Шар можно вписать в прямую призму, ЕСЛИ ее основания являются многоугольниками, описанными около окружности, а высота призмы равна диаметру этой окружности.
2. Радиус вписанного шара равен радиусу этой окружности.
3. Центр шара лежит на середине высоты призмы, соединяющей центры окружностей, вписанных с основания призмы.

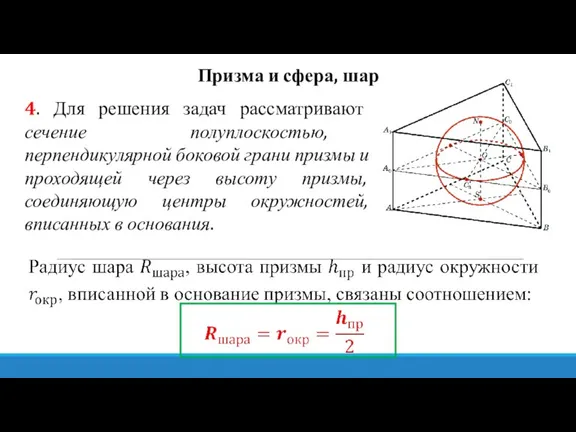
Призма и сфера, шар
4. Для решения задач рассматривают сечение полуплоскостью, перпендикулярной боковой грани призмы и проходящей через высоту призмы, соединяющую центры окружностей, вписанных в основания.

Призма и сфера, шар
1. Шар можно описать около призмы, если она прямая и ее основания являются многоугольниками, в писанными в окружность.
2. Центр шара лежит на середине высоты призмы, соединяющей центры окружностей, описанных около оснований призмы.
3. Для решения задач рассматривают сечение полуплоскостью, проходящей через центр шара и боковое ребро призмы.

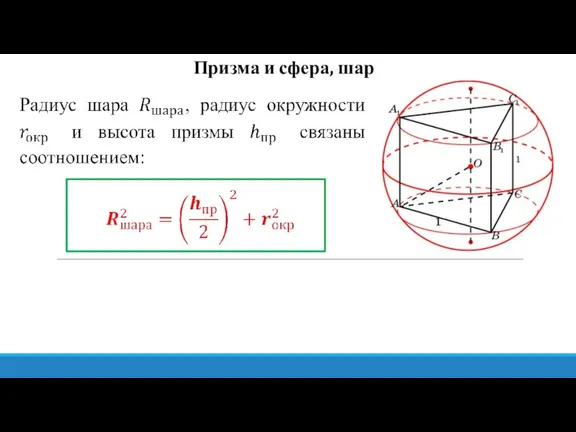
Призма и сфера, шар

Цилиндр и сфера, шар
1. Шар можно вписать ТОЛЬКО в такой цилиндр , высота которого равна диаметру основания (т.е. цилиндр – равносторонний).
2. Шар касается оснований цилиндра в их центрах и боковой поверхности цилиндра по окружности большого круга шара, параллельной основаниям цилиндра.
3. Большой круг шара вписан в осевое сечение цилиндра (т.е. в квадрат).

Цилиндр и сфера, шар
1. Шар можно описать около любого (прямого кругового) цилиндра.
2. Окружности оснований цилиндра лежат на поверхности шара.
3. Центр шара лежит на середине высоты, проходящей через ось цилиндра.
!!!4. Осевое сечение цилиндра (прямоугольник) вписано в окружность с радиусом, равным радиусу шара.

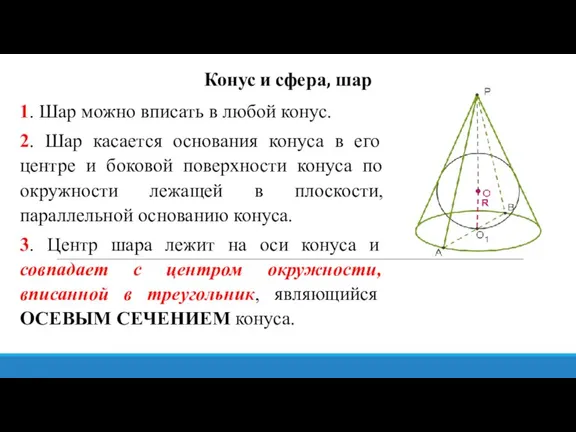
Конус и сфера, шар
1. Шар можно вписать в любой конус.
2. Шар касается основания конуса в его центре и боковой поверхности конуса по окружности лежащей в плоскости, параллельной основанию конуса.
3. Центр шара лежит на оси конуса и совпадает с центром окружности, вписанной в треугольник, являющийся ОСЕВЫМ СЕЧЕНИЕМ конуса.

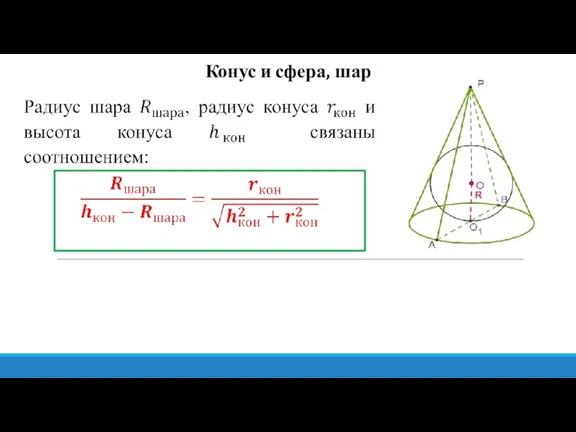
Конус и сфера, шар

Конус и сфера, шар
!!!4. В усеченный конус можно вписать сферу тогда и только тогда, когда сумма диаметров оснований равна удвоенной образующей конуса.
Ее ЦЕНТР СОВПАДАЕТ с центром окружности, вписанной в осевое сечение усеченного конуса.
Радиус сферы равен радиусу этой окружности

1. Шар можно описать около любого конуса.
2. Окружность основания конуса и вершина конуса лежат на поверхности шара.
3. Центр шара лежит на оси конуса и совпадает с центром окружности, описанной около треугольника, являющегося ОСЕВЫМ СЕЧЕНИЕМ конуса.
Конус и сфера, шар

Конус и сфера, шар

Примеры ключевых задач

КЛЮЧЕВАЯ ЗАДАЧА №1
В конус с радиусом основания, равным 3 см, и высотой, равной 4 см, вписан шар. Найдите отношение площади боковой поверхности конуса к площади поверхности шара.

КЛЮЧЕВАЯ ЗАДАЧА №2
Шар радиуса 6 описан около конуса. Высота конуса равна 8. Найдите площадь боковой поверхности конуса.