Кривые второго порядка гипербола и парабола

Гипербола имеет две асимптоты, уравнения которых
и
Если мнимая ось гиперболы направлена по оси Ох и имеет длину 2а, а действительная ось длиной 2b направлена по оси Оу (рис. 6)
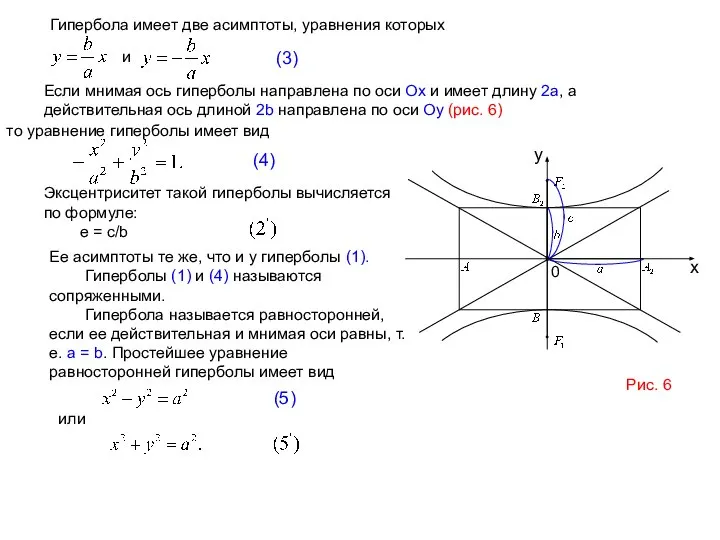
Рис. 6
x
y
0
(3)
то уравнение гиперболы имеет вид
(4)
Эксцентриситет такой гиперболы вычисляется по формуле:
е = с/b
Ее асимптоты те же, что и у гиперболы (1).
Гиперболы (1) и (4) называются сопряженными.
Гипербола называется равносторонней, если ее действительная и мнимая оси равны, т.е. а = b. Простейшее уравнение равносторонней гиперболы имеет вид
или
(5)

Задание 1. Найти оси, вершины, фокусы, эксцентриситет и уравнения асимптот гиперболы
Решение. Перенесем свободный член вправо и разделим на него все члены данного уравнения. В результате получим простейшее уравнение гиперболы
или
Сравнивая это уравнение с уравнением (1), имеем а = 3, b = 4. Таким образом, действительная ось гиперболы 2а = 6, а мнимая ось 2b = 8; координаты вершин
и
Далее,
следовательно, фокусами гиперболы служат точки
и
Эксцентриситет гиперболы вычисляем по формуле (2): е = с/а = 5/3. Наконец, подставляя значения а = 3, b = 4 в формулы (3), получаем уравнения асимптот гиперболы: у = 4х/3 и у = –4х/3.

Задание 2. Показать, что уравнение
Представляет собой уравнение гиперболы. Найти центр, оси, вершины, фокусы, эксцентриситет и асимптоты этой гиперболы.
Решение. Приведем данное уравнение к простейшему виду
Обозначим
и
Таким образом, мы производим преобразование параллельного переноса осей координат в точку О (–3;1). В новой системе координат данное уравнение принимает вид
т.е. определяет гиперболу с центром в точке
и полуосями
и
(рис. 7)
Рис. 7
y
0
x
Так как
то е = с/а = 3/2.
Нетрудно найти координаты вершин и фокусов в новой координатной системе:
Так как
то, возвращаясь к старой системе координат, получим
Остается найти асимптоты гиперболы. В новой системе координат уравнения асимптот имеют вид
т.е.
Заменяя теперь
на x + 3, а
на у – 1, получим уравнения асимптот в
первоначальной системе координат:

ПАРАБОЛА
Параболой называется множество точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой параболы.
Величина р, равная расстоянию от фокуса до директрисы, называется параметром параболы; прямая, проходящая через фокус параболы перпендикулярно ее директрисе, называется осью, а точка пересечения параболы с ее осью – вершиной параболы.
Простейшее уравнение параболы получается, если координатная система расположена следующим образом: за одну из координатных осей берется ось параболы, а за другую – прямая, перпендикулярная оси параболы и проведенная посредине между фокусом и директрисой.
Тогда уравнение параболы примет вид:
(рис. 8)
(рис. 9)
(рис. 10)
(рис. 11)
Рис. 8
Рис. 9
Рис. 10
Рис. 11
(1)
(2)
(3)
(4)

Уравнение
(5)
определяет параболу, ось которой перпендикулярна оси абсцисс.
Аналогично, уравнение
(6)
определяет параболу, ось которой перпендикулярна оси ординат.
Уравнения (5) и (6) приводятся к простейшему виду (1) – (4) путем тождественных преобразований с последующим параллельным переносом координатной системы.
Задание 1. Определить координаты фокуса и составить уравнение директрисы параболы
Решение. Сравнивая это уравнение с уравнением (1), находим, что
2p = 4, откуда p/2 = 1. Таким образом, точка F(1; 0) – фокус параболы, а прямая x + 1 = 0 – ее директриса.

Задание 2. Показать, что уравнение
Представляет собой уравнение параболы. Найти вершину, фокус, ось и директрису этой параболы.
Решение. Приведем данное уравнение к простейшему виду. Для этого выразим y через x и в полученном выражении выделим полный квадрат:
или
т.е.
Откуда
Следовательно,
или
Положим теперь
тем самым мы производим преобразование параллельного переноса координатных осей без изменения их направления в точку
В новой системе координат уравнение параболы примет вид: