Содержание
- 2. Какая из точек принадлежит графику функции y =10 – 5x И (1;5) К (5;10) Л (-1;10)
- 3. Какие из функций являются квадратичными З y = x3 + 5x + 6 И y =
- 4. Тема урока : Функция y = x2 , ее график и свойства Деятельность – единственный путь
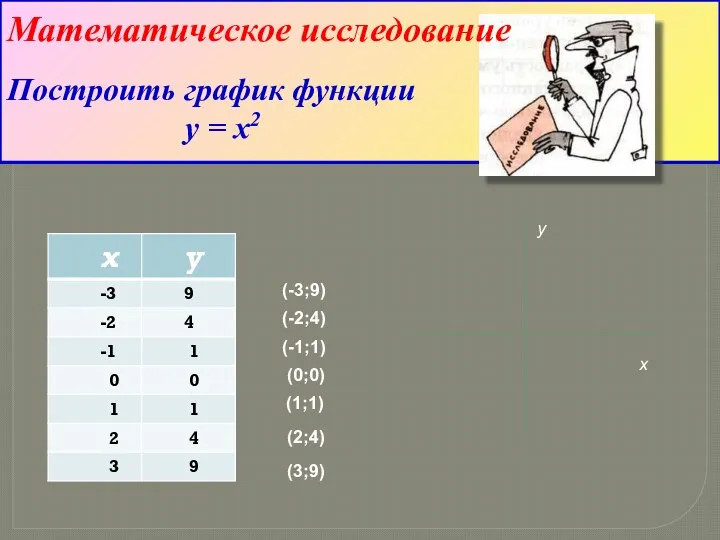
- 5. Построить график функции y = x2 Математическое исследование (-3;9) (-2;4) (-1;1) (0;0) (1;1) (2;4) (3;9) y
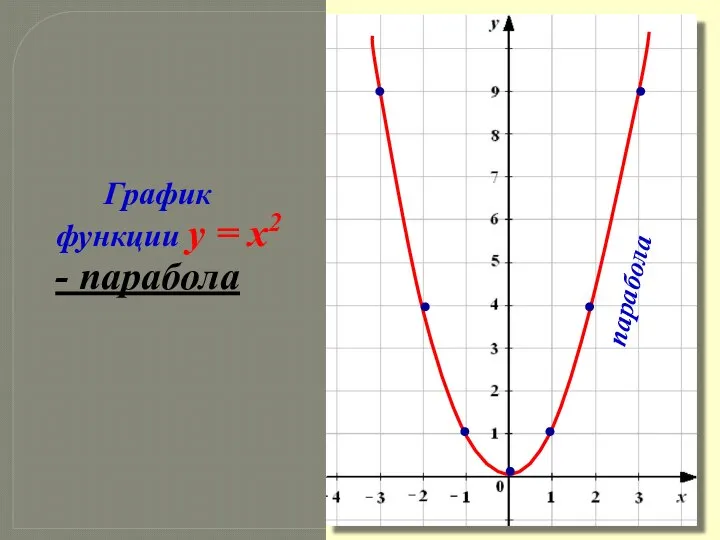
- 6. График функции y = x2 - парабола парабола
- 7. Свойства функции y = x2
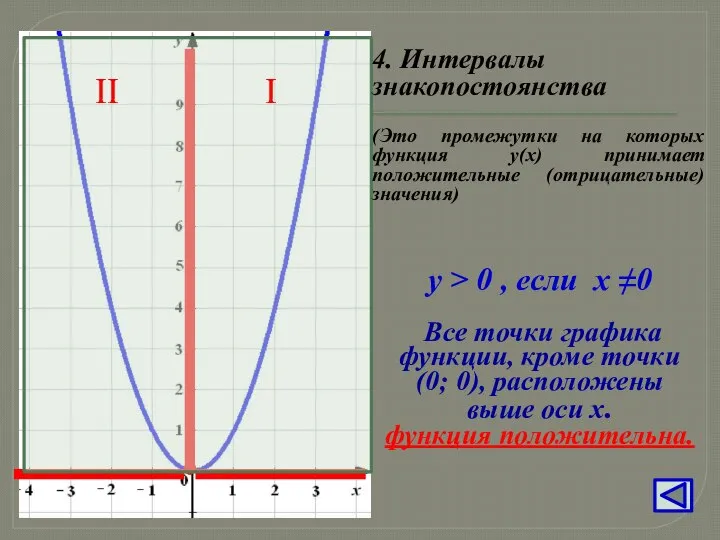
- 8. Схема исследования функции: Область определения Область значений Нули функции Интервалы знакопостоянства Промежутки монотонности Набольшее и наименьшее
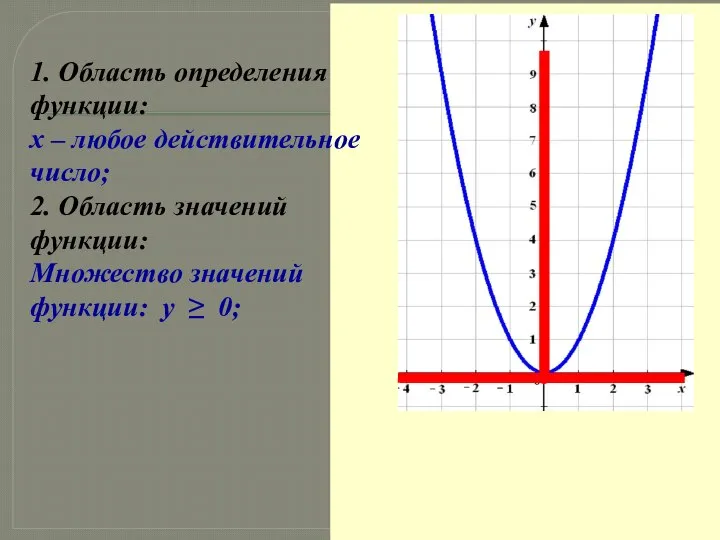
- 9. 1. Область определения функции: х – любое действительное число; 2. Область значений функции: Множество значений функции:
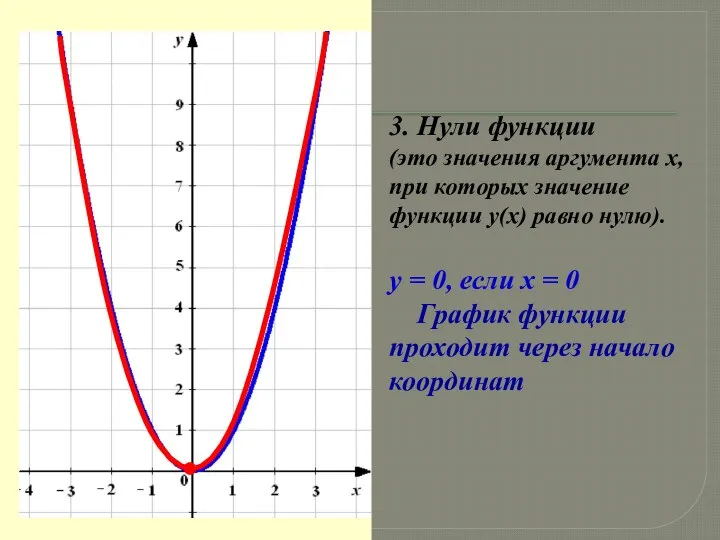
- 10. 3. Нули функции (это значения аргумента х, при которых значение функции у(х) равно нулю). y =
- 11. у > 0 , если х ≠0 Все точки графика функции, кроме точки (0; 0), расположены
- 12. 5. Монотонность функции Для неположительных значений Х функция y(х) убывает. - Убывает на промежутке от минус
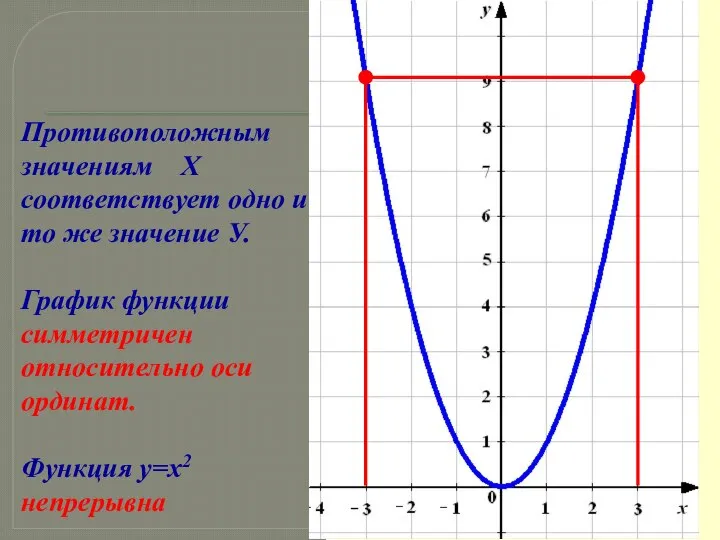
- 13. Противоположным значениям Х соответствует одно и то же значение У. График функции симметричен относительно оси ординат.
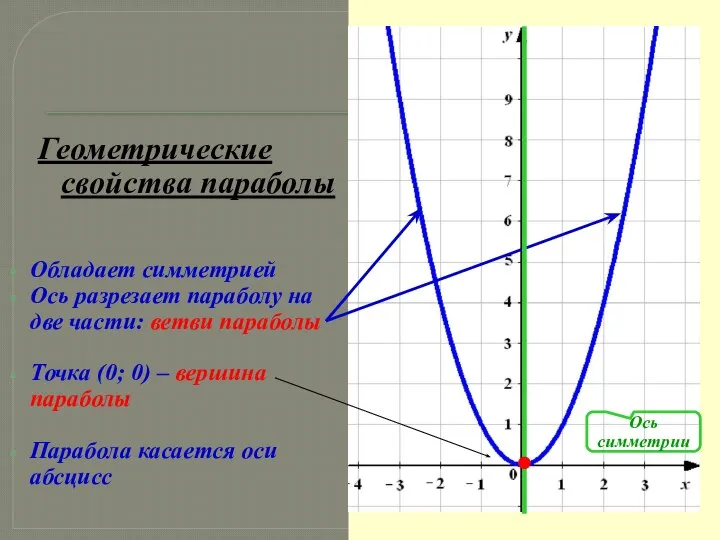
- 14. Геометрические свойства параболы Обладает симметрией Ось разрезает параболу на две части: ветви параболы Точка (0; 0)
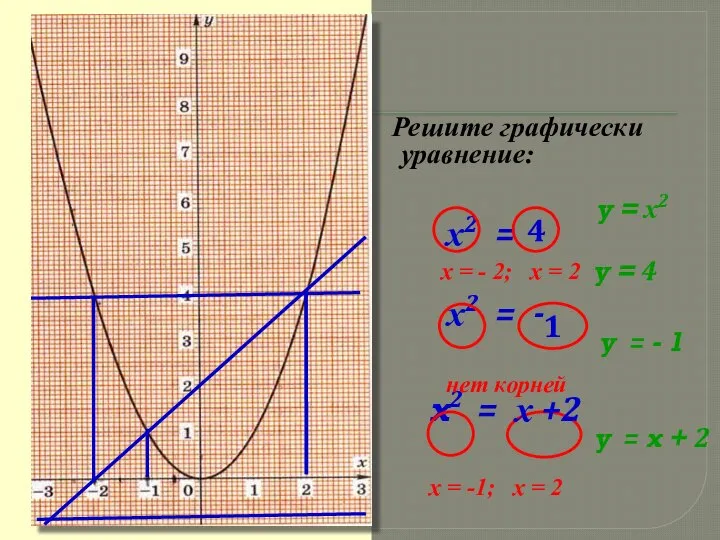
- 15. х = - 2; х = 2 Решите графически уравнение: х2 = х2 = - x2
- 17. Скачать презентацию






 Преемственность в формировании УПК младших школьников и учащихся 5-6 классов на уроках математики посредством интеграции
Преемственность в формировании УПК младших школьников и учащихся 5-6 классов на уроках математики посредством интеграции Геометрия Евклида
Геометрия Евклида Почему нельзя делить на ноль
Почему нельзя делить на ноль Определение синуса, косинуса, тангенса острого угла прямоугольного треугольника
Определение синуса, косинуса, тангенса острого угла прямоугольного треугольника Точка, отрезок, луч, прямая
Точка, отрезок, луч, прямая Интерактивная дидактическая игра Состав чисел до 10. Математика, 1 класс
Интерактивная дидактическая игра Состав чисел до 10. Математика, 1 класс Презентация на тему Дробные выражения (6 класс)
Презентация на тему Дробные выражения (6 класс)  Правило Лопиталя. Семинар 17
Правило Лопиталя. Семинар 17 Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля
Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля 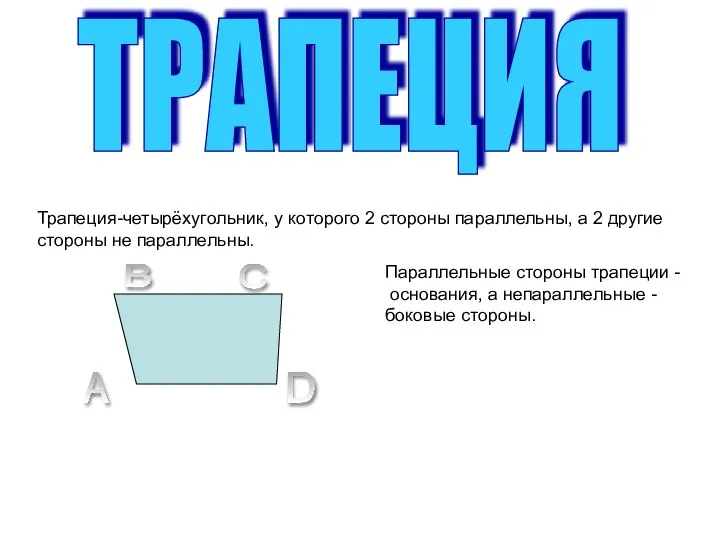 Трапеция
Трапеция Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Общее уравнение прямой и плоскости. Лекция1 (1)
Общее уравнение прямой и плоскости. Лекция1 (1) Умножение и деление десятичных дробей на натуральное число
Умножение и деление десятичных дробей на натуральное число Презентация на тему Понятие одночлена стандартный вид одночлена (7 класс)
Презентация на тему Понятие одночлена стандартный вид одночлена (7 класс)  Второй признак равенства треугольников. Урок 16
Второй признак равенства треугольников. Урок 16 Соотношения между сторонами и углами прямоугольного треугольника. Синус, косинус, тангенс и котангенс острого угла
Соотношения между сторонами и углами прямоугольного треугольника. Синус, косинус, тангенс и котангенс острого угла Решение примеров и уравнений
Решение примеров и уравнений L_3_U
L_3_U Презентация по математике "Число 5. Цифра 5" -
Презентация по математике "Число 5. Цифра 5" -  Цилиндр
Цилиндр Fraktaly_Osnovnye_ponyatia (1)
Fraktaly_Osnovnye_ponyatia (1) Действительные числа
Действительные числа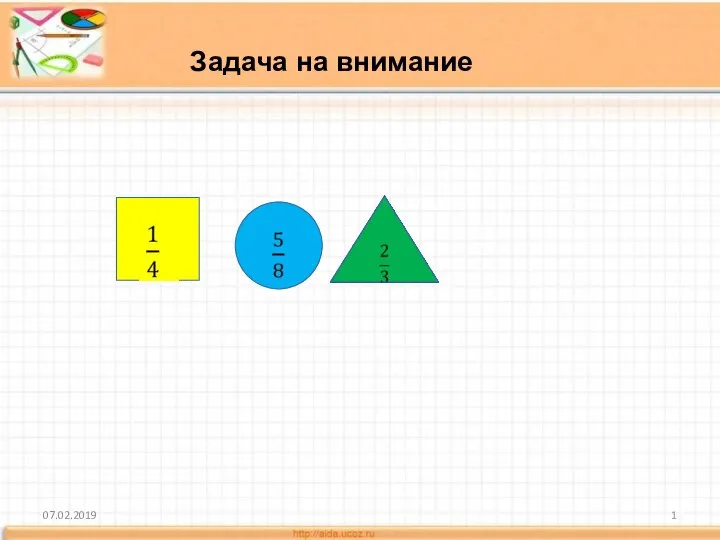 Задача на внимание. 5 класс
Задача на внимание. 5 класс Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота
Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота Площадь параллелограмма
Площадь параллелограмма Умножение двузначных чисел
Умножение двузначных чисел Число 5
Число 5 Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей