Слайд 2Уравнение , где a>0 (a ≠ 1), b>0 (b ≠ 1) будем

называть элементарным логарифмическим уравнением.
Областью определения его служит решение системы
При a = b мы получим уравнение f(x) = g(x), равносильное исходному.
Слайд 3При a = b мы получим уравнение f(x) = g(x), равносильное исходному.
При

a ≠ b решение уравнения сводится к решению уравнения
Что равносильно
Слайд 4При решении логарифмических уравнений с параметрами необходимо придерживаться следующей схемы:
1. Найти

область допустимых значений.
2. Решить уравнение (чаще всего выразить x через a).
3. Сделать перебор параметра a с учетом ОДЗ.
4. Проверить, удовлетворяют ли найденные корни уравнения условиям ОДЗ.
5. Записать ответ.
Слайд 5Типы логарифмических уравнений с параметром:
Уравнения, содержащие параметры в логарифмируемом выражении.
Уравнения, содержащие

параметры в основании.
Уравнения, содержащие параметры и в основании, и в логарифмируемом выражении.
Слайд 6
1. ОДЗ:
2.
3.
Ответ: решений нет.

Слайд 83. Корень уравнения x1= - 10 не удовлетворяет ОДЗ.
Ответ: a>0, a ≠

1, x =5
при a<0, a = 1, решений нет.
Слайд 9
1. ОДЗ.
2. Пусть , тогда наше уравнение сведется к квадратному:






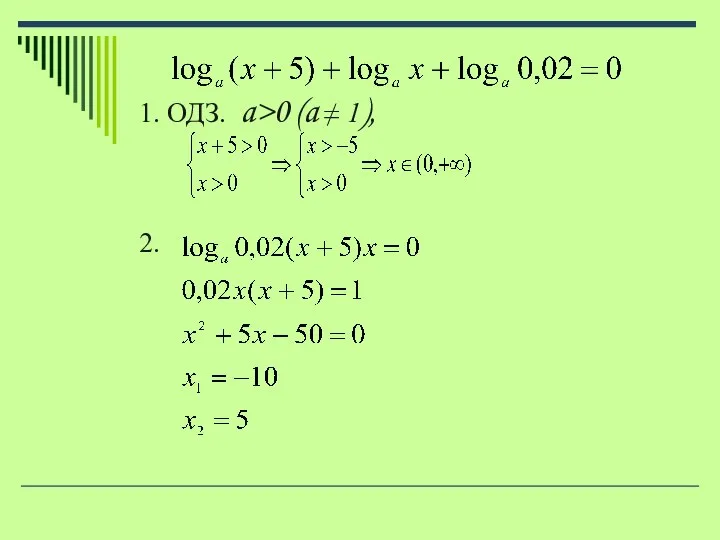


 Как называются числа при вычитании?
Как называются числа при вычитании? Делители числа. Наибольший общий делитель
Делители числа. Наибольший общий делитель Понятие логарифма
Понятие логарифма Группировка
Группировка Найди соседей. Дидактическая игра
Найди соседей. Дидактическая игра Тест по теме Окружность
Тест по теме Окружность Алгебраические уравнения
Алгебраические уравнения Методы отбора единиц наблюдения для выборочной совокупности. Возможные типы систематических ошибок оценки в исследованиях
Методы отбора единиц наблюдения для выборочной совокупности. Возможные типы систематических ошибок оценки в исследованиях Методологическое обеспечение экспериментальных исследований
Методологическое обеспечение экспериментальных исследований О числах
О числах Функция у = √х, ее свойства и график
Функция у = √х, ее свойства и график Координатная плоскость
Координатная плоскость Свойства и графики
Свойства и графики Классы интегрируемых функций
Классы интегрируемых функций Ортодромия и локсодромия
Ортодромия и локсодромия Схемы изонити
Схемы изонити Вероятность события есть количественная мера возможности наступления этого события
Вероятность события есть количественная мера возможности наступления этого события Деление и умножение
Деление и умножение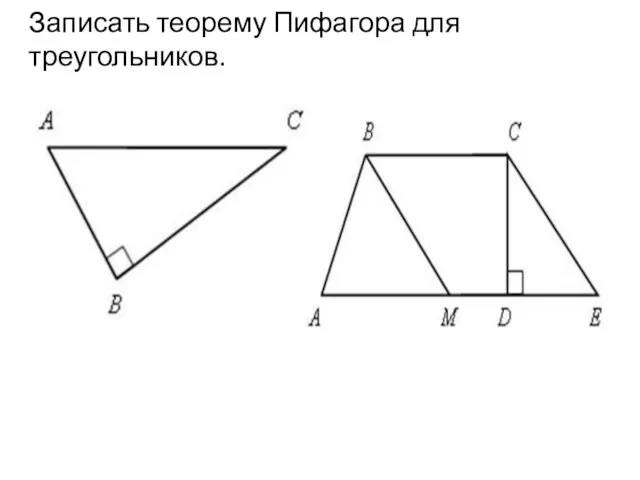 Теорема Пифагора. Урок 24
Теорема Пифагора. Урок 24 Векторный порядок. Дифференциальные операции второго порядка
Векторный порядок. Дифференциальные операции второго порядка Решение уравнений. Математика. 6 класс
Решение уравнений. Математика. 6 класс Задачи на разрезание
Задачи на разрезание Поліноми. Додавання поліномів
Поліноми. Додавання поліномів Семейство четырехугольников
Семейство четырехугольников Умножение десятичных дробей
Умножение десятичных дробей Фигуры вращения
Фигуры вращения Число и цифра 6
Число и цифра 6 ОГЭ. Приемы решения практико-ориентированных задач
ОГЭ. Приемы решения практико-ориентированных задач