Целые уравнения

продолжаем обобщать и углублять сведения об уравнениях;
знакомимся с понятием целого рационального и дробного рационального уравнения;
с понятием степени уравнения;
формируем навыки решения уравнений.;
контролируем уровень усвоения материала;
На уроке можем ошибаться, сомневаться, консультироваться.

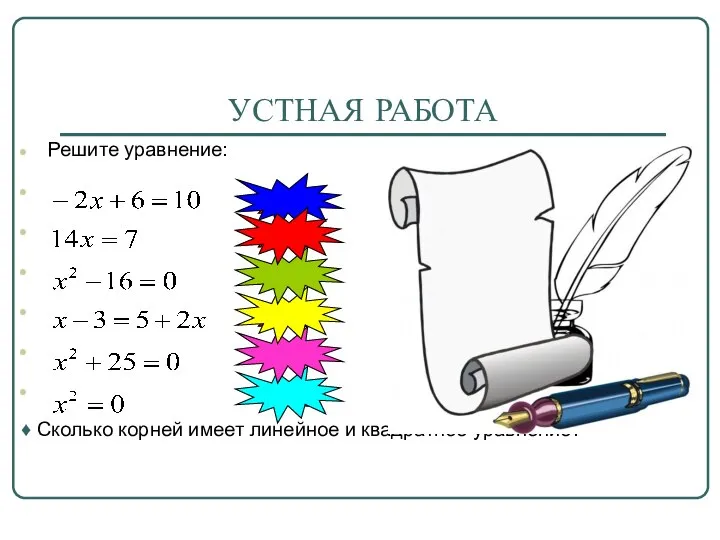
УСТНАЯ РАБОТА
Решите уравнение:
♦ Сколько корней имеет линейное и квадратное уравнение?
х=-2
корней нет
х=0
х=-8
х=-4;4
х=1/2

ЦЕЛЫЕ УРАВНЕНИЯ
(уравнения первой степени)
В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде и т.д. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.

ЦЕЛЫЕ УРАВНЕНИЯ
Новый великий прорыв в алгебре связан с именем французского ученого XVI в. Франсуа Виета. Он первым из математиков ввел буквенные обозначения для коэффициентов уравнения и неизвестных величин. А традицией обозначать неизвестные величины последними буквами латинского алфавита (x, y или z) мы обязаны его соотечественнику – Рене Декарту.
Ф. ВИЕТ
Р. ДЕКАРТ

ЦЕЛЫЕ УРАВНЕНИЯ
(уравнения второй степени)
Впервые квадратное уравнение сумели решить математики Древнего Египта. Формулу корней квадратного уравнения называют формулой Виета – по имени французского математика конца XVI в.

ЦЕЛЫЕ УРАВНЕНИЯ
(уравнения третьей степени)
Если квадратные уравнения умели решать еще математики Вавилонии и Древнего Египта, то кубические уравнения оказались «крепким орешком».
И всё же усилиями итальянских алгебраистов метод их решения был найден, а формула для их решения носит имя Кардано.

ЦЕЛЫЕ УРАВНЕНИЯ
(уравнения четвертой степени)
Метод решения уравнений четвертой степени нашёл в XV в. Лудовико Феррари, ученик Джерола-мо Кардано. Он так и называется – метод Феррари.

ЦЕЛЫЕ УРАВНЕНИЯ
(уравнения высших степеней)
А есть ли общие формулы для решения уравнений пятой степени и выше? Ответ на этот вопрос сумел найти норвежский математик Абель в начале XIX в., а чуть раньше его – итальянец Паоло Руффини: таких формул не существует.
РУФФИНИ
АБЕЛЬ

Одним из приемов решения уравнений высших степеней является
разложение на множители.
ПРИМЕР: решить уравнение .
Как называется способ, с помощью которого можно разложить левую часть уравнения на множители?
Когда произведение множителей равно 0?
Сколько корней имеет данное уравнение?
Как вы думаете, может ли уравнение третьей степени иметь 1, 2, 4, 5 корней или ни одного корня?
Способ группировки.
Когда хотя бы один из множителей равен 0.
Три корня.
Не более трех корней.

Другим приемом решения уравнений высших степеней является
введение новой переменной.
ПРИМЕР:
решить уравнение
Введем новую переменную:
Получим уравнение:
Решим данное уравнение:
Найдем переменную x:
y
y
или

САМОСТОЯТЕЛЬНАЯ РАБОТА
1 УРОВЕНЬ
№ 380 (а, б, в):
Ответы:
а) 1, -2, -10
б) -2, 2.5, 5
в) 2
2 УРОВЕНЬ
№ 380 (г, д, е)
Ответы:
г) 0, 0.1, 1
д) 5, -3
е) 0, 4

УСТНАЯ РАБОТА
Найдите корни уравнений:
Назовите степень каждого уравнения.
7
-2
-3
-4
-5
-6
-7
6
5
4
3
2
1
0
5
-1
2
2
-1
-5
-3
-2
-1
0
1
2
5

Итог урока.
Какое уравнение называется целым?
Что называется степенью уравнения?
Что называется корнем уравнения?
Сколько корней может иметь целое уравнение n-ой степени?
Определите степень уравнения.

Домашнее задание.
П.3.2, №378 (г, е), 382(2), 384(а, в) 385(а).