- Главная
- Математика
- математика

Содержание
- 2. ПОНЯТИЕ О КОМБИНАТОРИКЕ Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения
- 3. РАЗМЕЩЕНИЯ КОМБИНАТОРНЫХ КОНСТРУКЦИЙ В комбинаторике размеще́нием (из n по k) называется упорядоченный набор из k различных
- 4. ПЕРЕСТАНОВКА КОМБИНАТОРНЫХ КОНСТРУКЦИЙ В комбинаторике перестано́вка — это упорядоченный набор чисел 1, 2, n, обычно трактуемый
- 5. СОЧЕТАНИЯ КОМБИНАТОРНЫХ КОНСТРУКЦИЙ В комбинаторике сочетанием из n по k называется набор k элементов, выбранных из
- 6. ФОРМУЛА БИНОМА НЬЮТОНА Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы
- 8. Скачать презентацию
Слайд 2ПОНЯТИЕ О КОМБИНАТОРИКЕ
Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты,
ПОНЯТИЕ О КОМБИНАТОРИКЕ
Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты,

множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний (например, в генетике, информатике, статистической физике).
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.
Слайд 3РАЗМЕЩЕНИЯ КОМБИНАТОРНЫХ КОНСТРУКЦИЙ
В комбинаторике размеще́нием (из n по k) называется упорядоченный набор
РАЗМЕЩЕНИЯ КОМБИНАТОРНЫХ КОНСТРУКЦИЙ
В комбинаторике размеще́нием (из n по k) называется упорядоченный набор

из k различных элементов из некоторого множества различных n элементов.
Пример 1: 1,3,2,5 — это 4-элементное размещение из 6-элементного множества \{1,2,3,4,5,6 \}.
Пример 2: некоторые размещения элементов множества {1,2,3,4,5,6 } по 2: 1,2 1,3 1,4 1,5 … 2,1 2,3 учитывают порядок следования предметов. Так, например, наборы 2, 1, 3 и 3, 2, 1 являются различными, хотя состоят из одних и тех же элементов {1, 2, 3} (то есть совпадают как сочетания).
Пример 1: 1,3,2,5 — это 4-элементное размещение из 6-элементного множества \{1,2,3,4,5,6 \}.
Пример 2: некоторые размещения элементов множества {1,2,3,4,5,6 } по 2: 1,2 1,3 1,4 1,5 … 2,1 2,3 учитывают порядок следования предметов. Так, например, наборы 2, 1, 3 и 3, 2, 1 являются различными, хотя состоят из одних и тех же элементов {1, 2, 3} (то есть совпадают как сочетания).
Слайд 4ПЕРЕСТАНОВКА КОМБИНАТОРНЫХ КОНСТРУКЦИЙ
В комбинаторике перестано́вка — это упорядоченный набор чисел 1,
ПЕРЕСТАНОВКА КОМБИНАТОРНЫХ КОНСТРУКЦИЙ
В комбинаторике перестано́вка — это упорядоченный набор чисел 1,

2, n, обычно трактуемый как биекция на множестве { 1, 2n }, которая числу i ставит в соответствие i-й элемент из набора. Число n при этом называется порядком перестановки. Как синоним слову «перестановка» в этом смысле некоторые авторы используют слово расстановка
В теории групп под перестановкой произвольного множества подразумевается биекция этого множества на себя. Как синоним слову «перестановка» в этом смысле некоторые авторы используют слово подстановка.
Свойства: Число всех перестановок порядка n равно числу размещений из n по n, то есть факториалу:[1][2][3][4]
P_n=A_n^n= {n!}{(n-n)!}= {n!}{0!}=n!=1 2….. n.
Композиция определяет операцию произведения на перестановках одного порядка: Относительно этой операции множество перестановок порядка n образует группу, которую называют симметрической и обычно обозначают S_n.
Любая конечная группа порядка n изоморфна некоторой подгруппе группы перестановок из n чисел (теорема Кэли). При этом каждый элемент a \in G сопоставляется с перестановкой pi_a, задаваемой тождеством pi_a(g)=a 0 g, где g — произвольный элемент группы G, а — групповая операция.
В теории групп под перестановкой произвольного множества подразумевается биекция этого множества на себя. Как синоним слову «перестановка» в этом смысле некоторые авторы используют слово подстановка.
Свойства: Число всех перестановок порядка n равно числу размещений из n по n, то есть факториалу:[1][2][3][4]
P_n=A_n^n= {n!}{(n-n)!}= {n!}{0!}=n!=1 2….. n.
Композиция определяет операцию произведения на перестановках одного порядка: Относительно этой операции множество перестановок порядка n образует группу, которую называют симметрической и обычно обозначают S_n.
Любая конечная группа порядка n изоморфна некоторой подгруппе группы перестановок из n чисел (теорема Кэли). При этом каждый элемент a \in G сопоставляется с перестановкой pi_a, задаваемой тождеством pi_a(g)=a 0 g, где g — произвольный элемент группы G, а — групповая операция.
Слайд 5СОЧЕТАНИЯ КОМБИНАТОРНЫХ КОНСТРУКЦИЙ
В комбинаторике сочетанием из n по k называется набор k
СОЧЕТАНИЯ КОМБИНАТОРНЫХ КОНСТРУКЦИЙ
В комбинаторике сочетанием из n по k называется набор k

элементов, выбранных из данного множества, содержащего n различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Так, например, наборы (3-элементные сочетания, подмножества, k=3) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} (n=6) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.
В общем случае число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-й диагонали и n-й строки треугольника Паскаля
Число сочетаний из n по k равно биномиальному коэффициенту(см рисунок)
Так, например, наборы (3-элементные сочетания, подмножества, k=3) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} (n=6) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.
В общем случае число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-й диагонали и n-й строки треугольника Паскаля
Число сочетаний из n по k равно биномиальному коэффициенту(см рисунок)
Слайд 6ФОРМУЛА БИНОМА НЬЮТОНА
Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой
ФОРМУЛА БИНОМА НЬЮТОНА
Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой

неотрицательной степени суммы двух переменных, имеющая вид
Где — биномиальные коэффициенты, n — неотрицательное целое число.
В таком виде эта формула была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома Ньютона для более общего случая, когда показатель степени — произвольное действительное (или даже комплексное) число. В этом случае бином представляет собой бесконечный
Где — биномиальные коэффициенты, n — неотрицательное целое число.
В таком виде эта формула была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома Ньютона для более общего случая, когда показатель степени — произвольное действительное (или даже комплексное) число. В этом случае бином представляет собой бесконечный
 Вычисление площадей плоских фигур в прямоугольной системе координат (Лекция 3)
Вычисление площадей плоских фигур в прямоугольной системе координат (Лекция 3) Задача о расшивке узких мест производства
Задача о расшивке узких мест производства Внеклассное мероприятие. 5 класс
Внеклассное мероприятие. 5 класс Создание геометрических тел
Создание геометрических тел Содержание функциональной пропедевтики в начальной школе, 5–6-х классах, в начале курса алгебры
Содержание функциональной пропедевтики в начальной школе, 5–6-х классах, в начале курса алгебры История возникновения геометрии как науки
История возникновения геометрии как науки Решение задач
Решение задач Элементы теории обобщенных функций
Элементы теории обобщенных функций Презентация на тему НАХОЖДЕНИЕ СУММЫ НЕСКОЛЬКИХ СЛАГАЕМЫХ
Презентация на тему НАХОЖДЕНИЕ СУММЫ НЕСКОЛЬКИХ СЛАГАЕМЫХ  Степень с рациональным показателем. Множество рациональных чисел
Степень с рациональным показателем. Множество рациональных чисел Стереометрия. 1
Стереометрия. 1 Функция у=х в степени -n (n є N), их свойства и графики
Функция у=х в степени -n (n є N), их свойства и графики Неравенство треугольника
Неравенство треугольника Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых (4 класс)
Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых (4 класс) Алгоритм отыскания производной
Алгоритм отыскания производной Свойства квадратного корня
Свойства квадратного корня Степень с целым показателем ( урок обобщения и систематизации в форме игры крестики – нолики)
Степень с целым показателем ( урок обобщения и систематизации в форме игры крестики – нолики) Презентация на тему ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
Презентация на тему ЦЕНТРАЛЬНАЯ СИММЕТРИЯ  Презентация на тему РАЦИОНАЛЬНЫЕ ЧИСЛА
Презентация на тему РАЦИОНАЛЬНЫЕ ЧИСЛА  Понятие множество
Понятие множество Способы задания плоскости
Способы задания плоскости Интерактивная игра уроки математики в Школе Смешариков
Интерактивная игра уроки математики в Школе Смешариков Справедливые и несправедливые игры с точки зрения теории вероятностей
Справедливые и несправедливые игры с точки зрения теории вероятностей Занимательная математика. 2 класс
Занимательная математика. 2 класс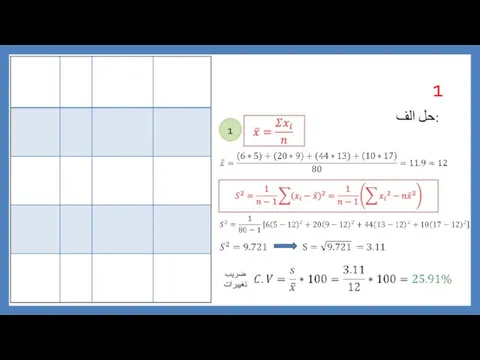 حل تمرین آمار
حل تمرین آمار История возникновения науки геометрии
История возникновения науки геометрии Презентация на тему История возникновения счета
Презентация на тему История возникновения счета  Prezentatsia_k_uroku_matematiki_v_6_kl
Prezentatsia_k_uroku_matematiki_v_6_kl