Содержание
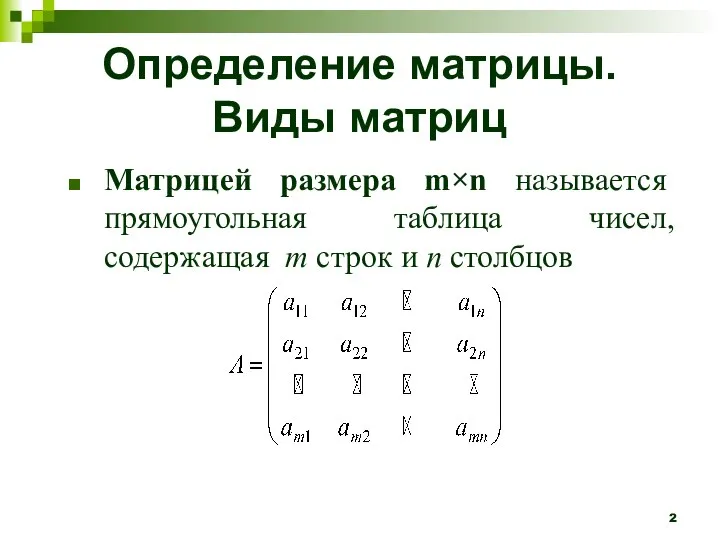
- 2. Определение матрицы. Виды матриц Матрицей размера m×n называется прямоугольная таблица чисел, содержащая m строк и n
- 3. Каждый элемент матрицы имеет два индекса: m – номер строки и n – номер столбца. Например,
- 4. Матрица называется квадратной n-го порядка, если она состоит из n строк и n столбцов. Матрица размера
- 5. Единичной называется квадратная матрица, элементы главной диагонали которой равны 1, а все остальные элементы равны 0:
- 6. Транспонированной матрицей для матрицы A называется матрица AT, строки которой являются столбцами матрицы , а столбцы
- 7. Линейные операции над матрицами Суммой матриц и называется матрица . Складываются матрицы только одинакового размера.
- 8. Например. Найти сумму и разность матриц А и В:
- 9. Произведением матрицы А на число λ называется матрица . Другими словами, для умножения матрицы на число
- 10. Например: Умножая матрицу на число 2, получим:
- 11. Для любых матриц одинакового размера и любых чисел выполняются следующие свойства: 1 2 3 4 5
- 12. Умножение матриц Произведением матрицы на матрицу называется матрица C размера с элементами , , . Другими
- 13. В самом определении произведения матриц заложено, что число столбцов первой матрицы должно совпадать с числом строк
- 14. Ряд свойств операции умножения матриц Если A, B и C - квадратные матрицы одного порядка, то
- 15. Например, Найти произведение матриц: Число столбцов первой матрицы равно числу строк второй, следовательно их произведение существует:
- 16. Определители второго и третьего порядков. Их свойства Понятие определителя вводится только для квадратных матриц. Рассмотрим квадратную
- 17. Пусть – матрица 3го порядка. Минором элемента называется определитель , составленный из элементов, оставшихся после вычеркивания
- 18. Определителем 3го порядка (матрицы ) называется сумма произведений элементов первой строки матрицы на их алгебраические дополнения.
- 19. Примеры вычисления определителей
- 20. Схемы вычисления определителей
- 21. Свойства определителей: Определитель не меняется при транспонировании. Если все элементы какой-либо строки (или столбца) равны нулю,
- 22. Справедливо равенство Определитель не изменится, если к элементам какой-либо его строки (столбца) прибавить элементы другой строки
- 23. Числовые примеры свойств 1 и 2:
- 24. Числовые примеры свойства 3:
- 25. Числовые примеры свойств 4 и 5:
- 26. Числовые примеры свойства 6:
- 27. Числовые примеры свойства 7:
- 28. Числовые примеры свойства 8:
- 29. Числовые примеры свойства 9 :
- 30. Обратная матрица Матрица называется обратной к квадратной матрице A, если Матрица называется вырожденной, если ; в
- 31. Пример: Найти обратную матрицу для Имеем: Таким образом:
- 32. Тогда Вычисляя определитель матрицы A, получаем |A|=29. Теперь по формуле:
- 33. Теорема Если A и B невырожденные квадратные матрицы одинакового порядка, то
- 34. Ранг матрицы Рассмотрим матрицу A размера m×n : Выберем в матрице A произвольно k строк и
- 35. Метод вычисления ранга матрицы При вычислении ранга матрицы нужно переходить от миноров меньших порядков к минорам
- 36. Теорема о ранге матрицы Ранг матрицы равен максимальному числу ее линейно независимых строк (столбцов) (rangA или
- 37. Свойства ранга матрицы Если матрица A имеет размеры m×n, то тогда и только тогда, когда все
- 38. Элементарные преобразования матрицы Отбрасывание нулевой строки (столбца) матрицы Умножение всех элементов строки(столбца) матрицы на число ,
- 39. Элементарные преобразования не меняют ранг матрицы. С помощью элементарных преобразований матрицу можно привести к ступенчатому виду:
- 40. Домашнее задание
- 41. Даны матрицы А и В. Найти их сумму и разность
- 42. Дана матрица А. Найти 2А (умножить матрицу А на 2)
- 44. Скачать презентацию








































 Призма и антипризма
Призма и антипризма Riešenie rovníc, ak je neznáma na oboch stranách rovnice
Riešenie rovníc, ak je neznáma na oboch stranách rovnice Презентация на тему Окружность, ее центр и радиус
Презентация на тему Окружность, ее центр и радиус  Ознакомление с составной задачей
Ознакомление с составной задачей Презентация на тему Внетабличное умножение и деление. Приём деления для случаев вида 782, 693
Презентация на тему Внетабличное умножение и деление. Приём деления для случаев вида 782, 693  Градиентные методы
Градиентные методы Математика. Задачи на кратное сравнение
Математика. Задачи на кратное сравнение Презентация на тему Смешанные числа (5 класс)
Презентация на тему Смешанные числа (5 класс)  Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Давай посчитаем. Свинки на тропинке
Давай посчитаем. Свинки на тропинке Приближение десятичных дробей
Приближение десятичных дробей Область определения выражения
Область определения выражения Скалярное произведение векторов
Скалярное произведение векторов Проект по математике Задачи-расчеты из моей жизни
Проект по математике Задачи-расчеты из моей жизни Сочетания. Задачи
Сочетания. Задачи Решение задач с помощью уравнений
Решение задач с помощью уравнений ЛP№1_Симплекс-метод окон
ЛP№1_Симплекс-метод окон Реализация преемственности между начальной школой и основной в обучении математики
Реализация преемственности между начальной школой и основной в обучении математики Случайные величины
Случайные величины Сложение в пределах 20
Сложение в пределах 20 Делимость суммы на натуральное число
Делимость суммы на натуральное число Открытия науки в России 10-12 в
Открытия науки в России 10-12 в Презентация на тему Обозначение натуральных чисел
Презентация на тему Обозначение натуральных чисел  Человек и число
Человек и число Размещения. Формула размещения
Размещения. Формула размещения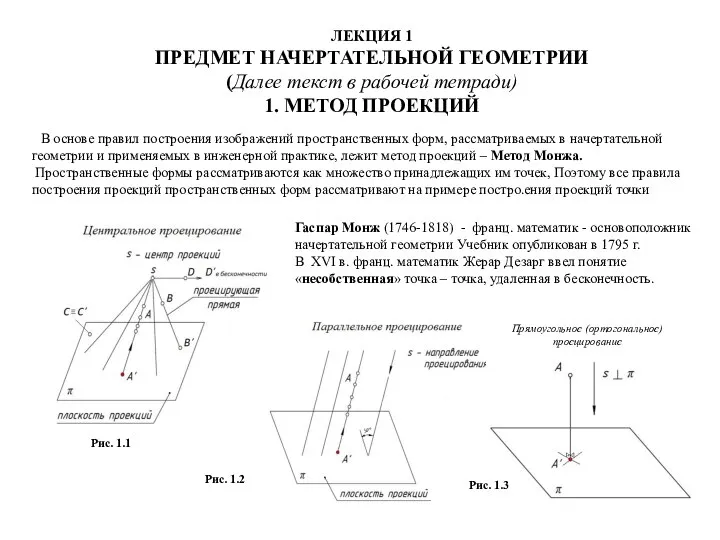 Предмет начертательной геометрии. Метод проекций. (Лекция 1)
Предмет начертательной геометрии. Метод проекций. (Лекция 1) Математический словарь
Математический словарь Созвездия. Сималтиниус Раунд Тэйбл
Созвездия. Сималтиниус Раунд Тэйбл