Метод решения систем линейных уравнений методом Крамера

Габриель Крамер
швейцарский математик
31.08.1704 – 04.01.1752
Крамер родился в семье франкоязычного врача. С раннего возраста показал большие способности в области математики. В 18 лет защитил диссертацию. В 20-летнем возрасте Крамер выставил свою кандидатуру на должность преподавателя на кафедре философии Женевского университета.
Самая известная из работ Крамера —трактат «Введение в анализ алгебраических кривых» 1750 году. Для доказательства Крамер строит систему линейных уравнений и решает её с помощью алгоритма, названного позже его именем: метод Крамера

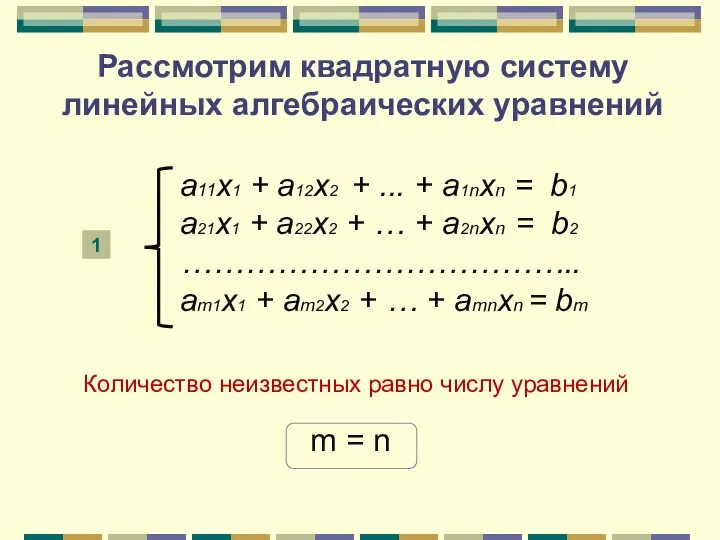
Рассмотрим квадратную систему линейных алгебраических уравнений
а11x1 + а12x2 + ... + а1nxn = b1
a21x1 + a22x2 + … + a2nxn = b2
………………………………..
am1x1 + am2x2 + … + amnxn = bm
1
Количество неизвестных равно числу уравнений
m = n

А – основная матрица системы
Х – матрица-столбец неизвестных
В – матрица-столбец свободных членов
А =
а11 а12 ... a1n
a21 a22 … a2n
.....................
am1 am2 … amn
X =
X1
X2
….
Xn
B =
b1
b2
….
bm
АХ = В
- запись СЛАУ в матричном виде
Вспомним такие понятия как:

Метод Крамера
Решение системы квадратных линейных уравнений AX= B , где количество неизвестных равно количеству уравнений данной системы,
с невырожденной квадратной матрицей А - единственно и имеет вид :
Х1 =
Δ1
Δ
, Х2 =
Δ2
Δ
, Х3 =
Δ3
Δ
, .... , Хn =
Δn
Δ
Х1, Х2 , Х3 ,…, Хn - неизвестные переменные, значения которых надо найти, а
Δ ; Δ1 ; Δ2 ; Δ3 ; .... ; Δn – определители, которые нужно составить по методу Крамера, а затем вычислить

Δ =
а11 а12 ... a1n
a21 a22 … a2n
.....................
am1 am2 … amn
- определитель системы, определитель основной матрицы
Δ1 =
b1 а12 ... a1n
b2 a22 … a2n
.....................
bm am2 … amn
-получается из главного определителя заменой 1-го столбца столбцом свободных членов
1) Составим главный определитель - Δ
2) Составим определитель - Δ1

3) Составим определитель - Δ2
Δ2 =
а11 b1 ... a1n
a21 b2 … a2n
.....................
am1 bm … amn
получается из главного определителя заменой 2-го столбца столбцом свободных членов.
3) Составим определитель - Δn
Δn =
а11 а12 ... b1
a21 a22 … b2
.....................
am1 am2 … bm
получается из главного определителя заменой n-го столбца столбцом свободных членов

Рассмотрим пример 1
Задание.
Решите систему линейных
уравнений методом Крамера
2Х1 – Х2 = 0
Х1 + 3Х2 = 7
Решение.
Основная матрица системы имеет вид
1) Вычислим ее определитель
А =
-1
1 3
Δ =
-1
1 3
= 6 + 1 = 7
Δ - отличен от нуля система имеет единственное решение, которое может быть найдено методом Крамера.

2) Составим и вычислим необходимые определители
Δ1 =
0 -1
7 3
= 7 ;
Δ2 =
= 14 ;
0
1 7
3) Находим неизвестные переменные по формулам
Х1 =
Δ1
Δ
=
7
7
= 1
Х2 =
Δ2
Δ
=
14
7
= 2
Ответ: Х1 = 1, Х2 = 2.

Рассмотрим пример 2
Задание.
Решите систему линейных
уравнений методом Крамера
Решение.
Основная матрица системы имеет вид
1) Вычислим ее определитель

Так как определитель основной матрицы системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера.
2) Составим и вычислим необходимые определители
Δ1 =
3 -1
-2 1
2 0 2
= -36 + 6 + 0 – 4 – 18 – 0 = - 52
Δ2 =
2 9 -1
1 3 1
1 2 2
= 12 + 9 – 2 + 3 -18 – 4 = 0
Δ3 =
2 3 9
1 -2 3
1 0 2
= -8 + 9 + 0 +18 – 6 – 0 = 13

3) Находим неизвестные переменные по формулам
Х1 =
Δ1
Δ
=
-52
-13
= 4
Х2 =
Δ2
Δ
=
0
-13
= 0
Х3 =
Δ3
Δ
= 13
-13
= -1
Ответ: Х1 = 4, Х2 = 0, Х3 = -1.

Рассмотрим пример 3
Задание.
Решите систему линейных
уравнений методом Крамера
Решение.
Основная матрица системы имеет вид
1) Вычислим ее определитель
А =
-1 1
1 -1
1 -2 1
Δ =
-1 1
1 -1
1 -2 1
= 2 - 2 + 1 - 1 - 4 + 1 = -3

Так как определитель основной матрицы системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера.
2) Составим и вычислим необходимые определители
Δ1 =
4 -1 1
2 1 -1
1 -2 1
= -6
Δ2 =
2 4 1
1 2 -1
1 1 1
= -3
Δ3 =
2 -1 4
1 1 2
1 -2 1
= -2
3) Находим неизвестные переменные по формулам
Х1 =
Δ1
Δ
Х2 =
Δ2
Δ
Х3 =
Δ3
Δ
= 2 ;
= 1 ;
= 1
Ответ: Х1 = 2, Х2 = 1, Х3 = 1.

Рассмотрим пример 4
Задание.
Решите систему линейных
уравнений методом Крамера
Решение.
Основная матрица системы имеет вид
1) Вычислим ее определитель
А =
1 5 -1
2 -1 1
1 2 -3
Δ =
= 31
1 5 -1
2 -1 1
1 2 -3
Δ - отличен от нуля система имеет единственное решение, которое может быть найдено методом Крамера.

2) Составим и вычислим необходимые определители
Δ1 =
= 31
Δ2 =
= 0
Δ3 =
= 31
3) Находим неизвестные переменные по формулам
Х1 =
Δ1
Δ
Х2 =
Δ2
Δ
Х3 =
Δ3
Δ
= 1 ;
= 0 ;
= 1
Ответ: Х1 = 1, Х2 = 0, Х3 = 1.
0 5 -1
3 -1 1
-2 2 -3
1 0 -1
2 3 1
1 -2 -3
1 5 0
2 -1 3
1 2 -2
31
31
=
0
31
=
31
31
=