- Главная
- Математика
- Методы решения тригонометрических уравнений. 10 класс

Содержание
Слайд 3
Решение уравнений, сводящихся к квадратным уравнениям
Решение уравнений, сводящихся к квадратным уравнениям

Слайд 4Уравнения вида a sin x + b cos x = 0, где a
Уравнения вида a sin x + b cos x = 0, где a

и b – некоторые числа, называются однородными уравнениями первой степени относительно sin x или cos x.
Рассмотрим уравнение
sin x – cos x = 0. Разделим обе части уравнения на cos x. Так можно сделать, потери корня не произойдёт, т.к. , если cos x = 0, то sin x = 0. Но это противоречит основному тригонометрическому тождеству
sin2 x + cos2 x = 1.
Получим tg x – 1 = 0.
tg x = 1,
дорешать
Рассмотрим уравнение
sin x – cos x = 0. Разделим обе части уравнения на cos x. Так можно сделать, потери корня не произойдёт, т.к. , если cos x = 0, то sin x = 0. Но это противоречит основному тригонометрическому тождеству
sin2 x + cos2 x = 1.
Получим tg x – 1 = 0.
tg x = 1,
дорешать
Решение однородных тригонометрических уравнений
1 степени
Слайд 5
Решение однородных уравнений второй степени
Решение однородных уравнений второй степени

- Предыдущая
Тривиальные названияСледующая -
Николай Коперник
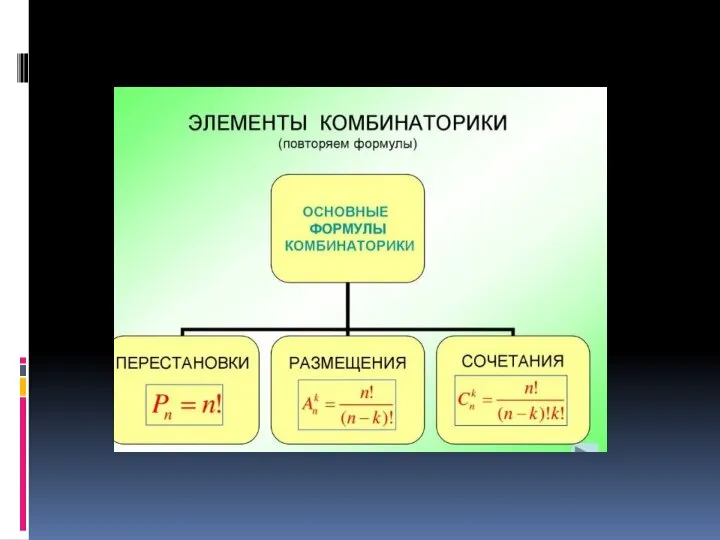 Основные понятия комбинаторики
Основные понятия комбинаторики Открытый урок «Математический бой» 11класс
Открытый урок «Математический бой» 11класс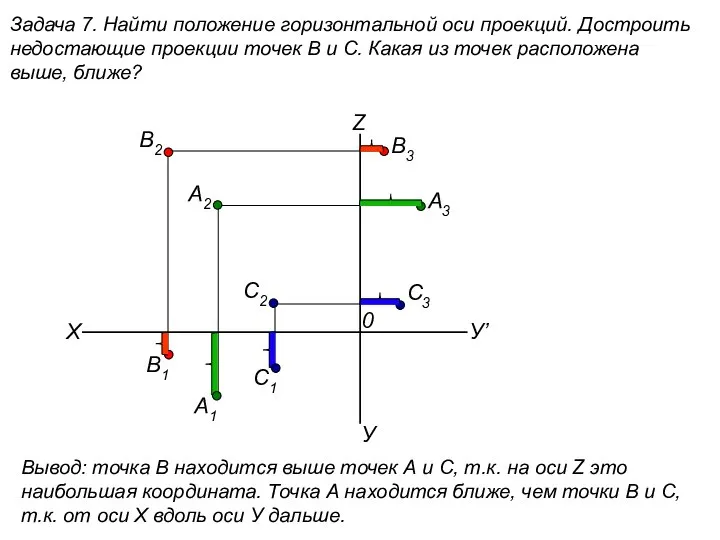 Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7)
Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7) Движения. 9-й класс
Движения. 9-й класс Математика. Закрепление изученного материала. 4 класс
Математика. Закрепление изученного материала. 4 класс Теорема Гаусса-Остроградского
Теорема Гаусса-Остроградского Статистика. Необходимость возникновения статистики-науки
Статистика. Необходимость возникновения статистики-науки Устный счёт Прицепи вагоны. 2 класс
Устный счёт Прицепи вагоны. 2 класс Понятие математической индукции и ее применение
Понятие математической индукции и ее применение Решение логических задач
Решение логических задач Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Презентация на тему Многогранники. Призма
Презентация на тему Многогранники. Призма  Определенный интеграл. Решение примеров на нахождение первообразных и интегралов
Определенный интеграл. Решение примеров на нахождение первообразных и интегралов Практикум №5. Сквозной пример
Практикум №5. Сквозной пример Тест-тренажёр для учащихся 2 классов. Знакомство с математическими терминами. Сумма и разность
Тест-тренажёр для учащихся 2 классов. Знакомство с математическими терминами. Сумма и разность Деление дробей
Деление дробей Применение производной к исследованию функции
Применение производной к исследованию функции Найди значение выражения. Реши задачу
Найди значение выражения. Реши задачу Как умножали египтяне
Как умножали египтяне Правильные многогранники
Правильные многогранники Предел функции в точке и на бесконечности. Предел числовой последовательности
Предел функции в точке и на бесконечности. Предел числовой последовательности Математика. Управление социальными системами. Математический анализ. Дифференцирование функции одной переменной
Математика. Управление социальными системами. Математический анализ. Дифференцирование функции одной переменной Презентация на тему Транспортир. Измерение углов транспортиром
Презентация на тему Транспортир. Измерение углов транспортиром  Формулы сокращённого умножения: квадрат разности и квадрат суммы
Формулы сокращённого умножения: квадрат разности и квадрат суммы Презентация на тему Степенная функция
Презентация на тему Степенная функция  Интересные факты про математику
Интересные факты про математику Презентация по математике. Исторические сведения
Презентация по математике. Исторические сведения Задачи на площадь
Задачи на площадь