Изображение пространственных фигур на плоскости

Итак, мы приступили к изучению стереометрии – геометрии в пространстве. Как всегда нам необходимо уметь изображать геометрические фигуры, причем все чертежи мы по-прежнему выполняем на плоскости (на странице тетради, на доске и т.д.). Каким образом пространственную фигуру (например, куб) можно «уложить» в плоскость?
Для решения этой задачи применяется метод параллельного проектирования. Выясним его суть на примере простейшей геометрической фигуры – точки.
Итак, у нас есть геометрическая фигура в пространстве – точка А.
А

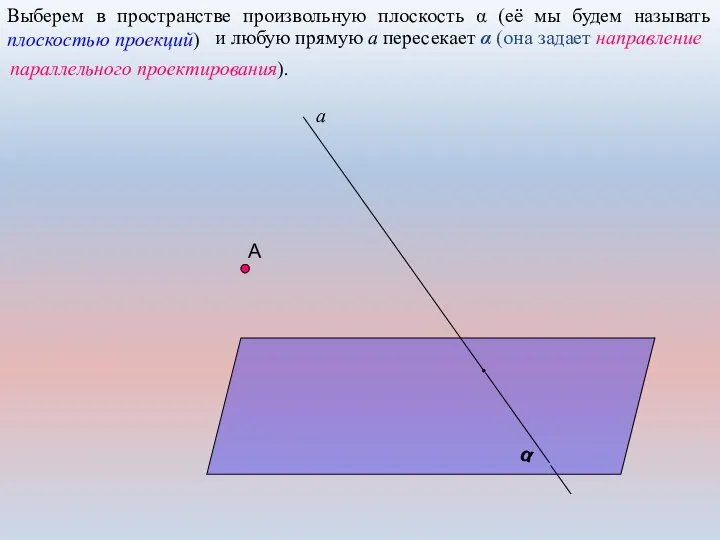
А
Выберем в пространстве произвольную плоскость α (её мы будем называть плоскостью проекций)
α
и любую прямую a пересекает α (она задает направление
параллельного проектирования).
а

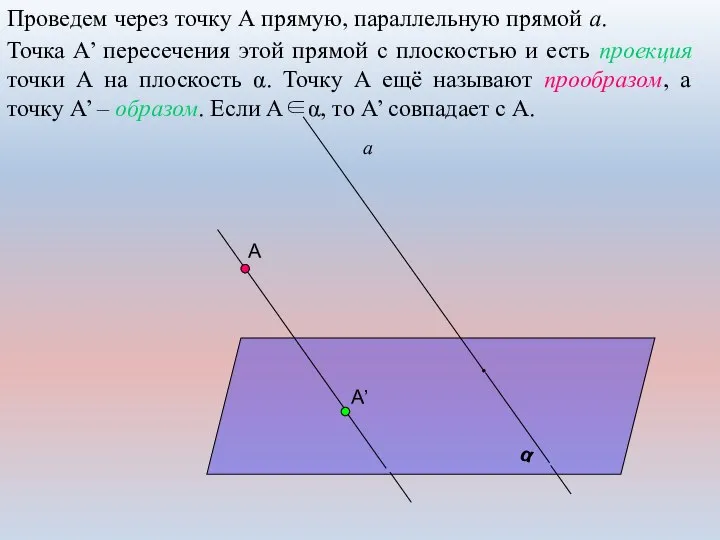
А
α
а
Проведем через точку А прямую, параллельную прямой а.
А’
Точка А’ пересечения этой прямой с плоскостью и есть проекция точки А на плоскость α. Точку А ещё называют прообразом, а точку А’ – образом. Если А∈α, то А’ совпадает с А.

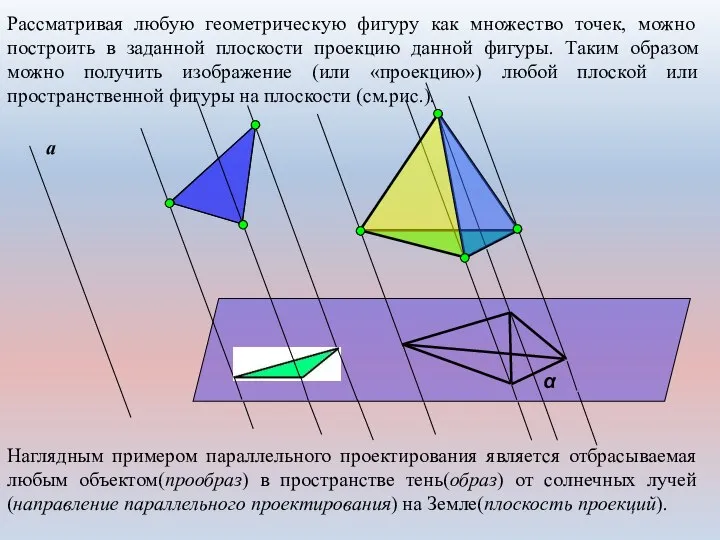
Рассматривая любую геометрическую фигуру как множество точек, можно построить в заданной плоскости проекцию данной фигуры. Таким образом можно получить изображение (или «проекцию») любой плоской или пространственной фигуры на плоскости (см.рис.).
а
α
Наглядным примером параллельного проектирования является отбрасываемая любым объектом(прообраз) в пространстве тень(образ) от солнечных лучей(направление параллельного проектирования) на Земле(плоскость проекций).

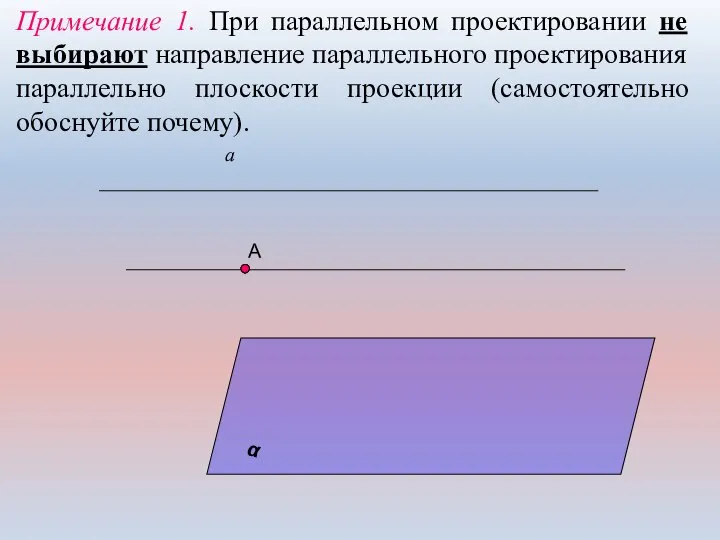
Примечание 1. При параллельном проектировании не выбирают направление параллельного проектирования параллельно плоскости проекции (самостоятельно обоснуйте почему).
А
а
α

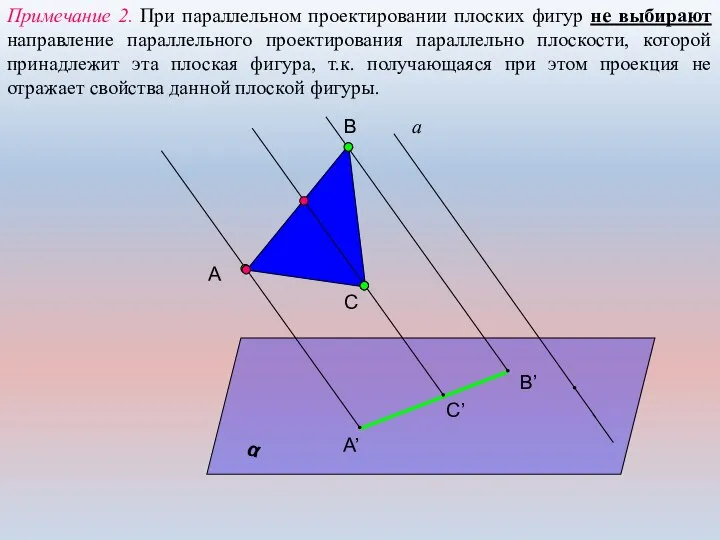
Примечание 2. При параллельном проектировании плоских фигур не выбирают направление параллельного проектирования параллельно плоскости, которой принадлежит эта плоская фигура, т.к. получающаяся при этом проекция не отражает свойства данной плоской фигуры.
А
а
α
B
C
А’
B’
C’

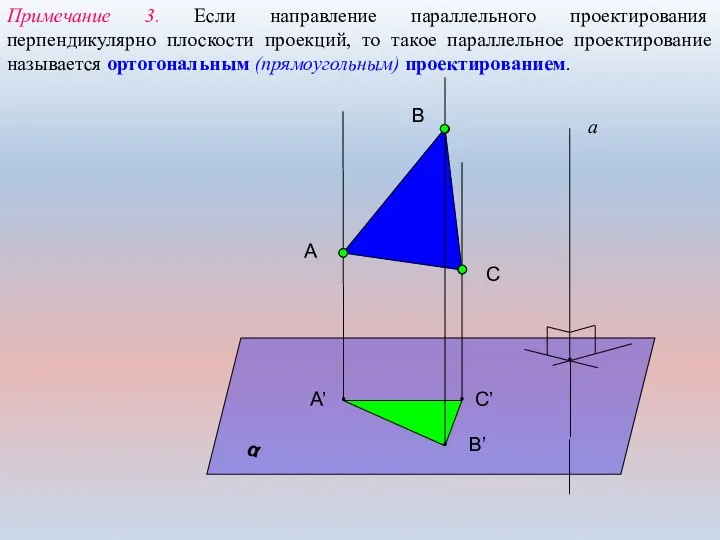
Примечание 3. Если направление параллельного проектирования перпендикулярно плоскости проекций, то такое параллельное проектирование называется ортогональным (прямоугольным) проектированием.
А
а
α
B
C
А’
B’
C’

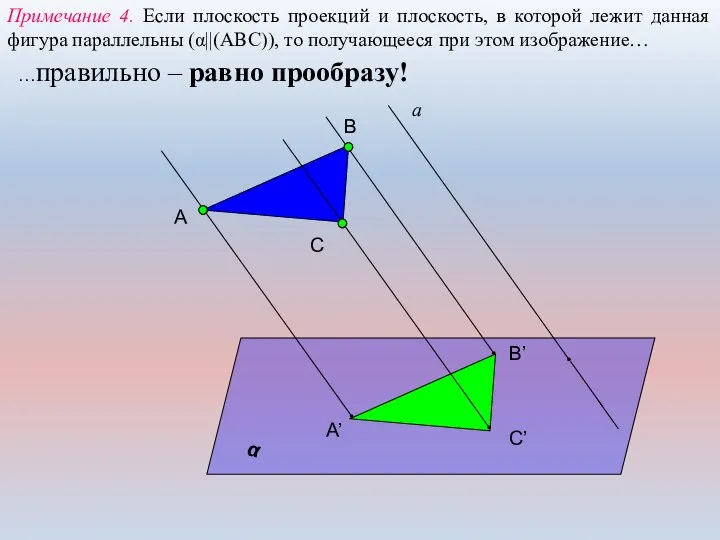
Примечание 4. Если плоскость проекций и плоскость, в которой лежит данная фигура параллельны (α||(АВС)), то получающееся при этом изображение…
А
а
α
B
C
А’
B’
C’
…правильно – равно прообразу!

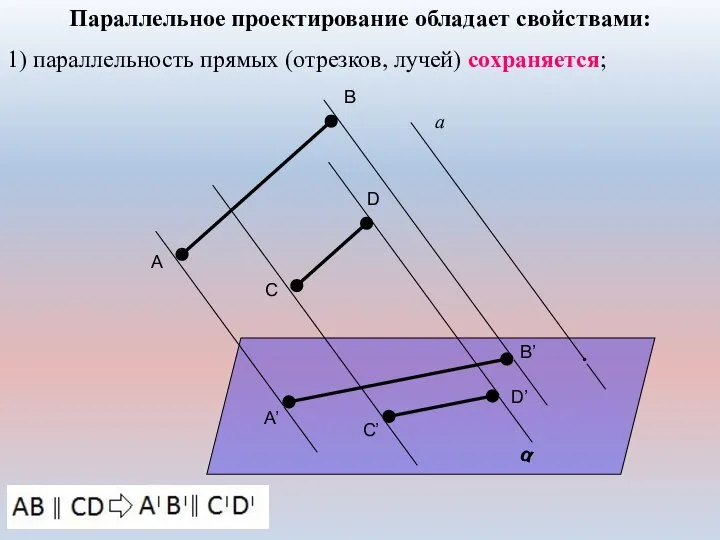
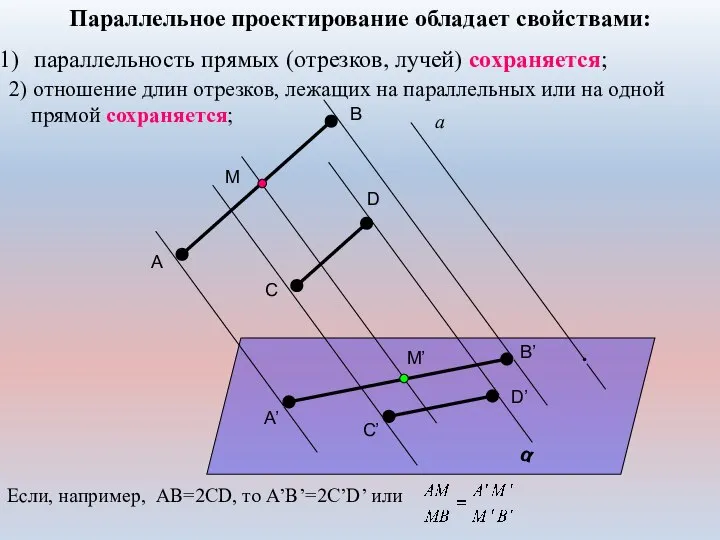
Параллельное проектирование обладает свойствами:
1) параллельность прямых (отрезков, лучей) сохраняется;
α
а
A
D
C
B
A’
D’
C’
B’

2) отношение длин отрезков, лежащих на параллельных или на одной прямой сохраняется;
Параллельное проектирование обладает свойствами:
параллельность прямых (отрезков, лучей) сохраняется;
α
а
A
D
C
B
A’
D’
C’
B’
Если, например, АВ=2CD, то А’В’=2C’D’ или
М
М’

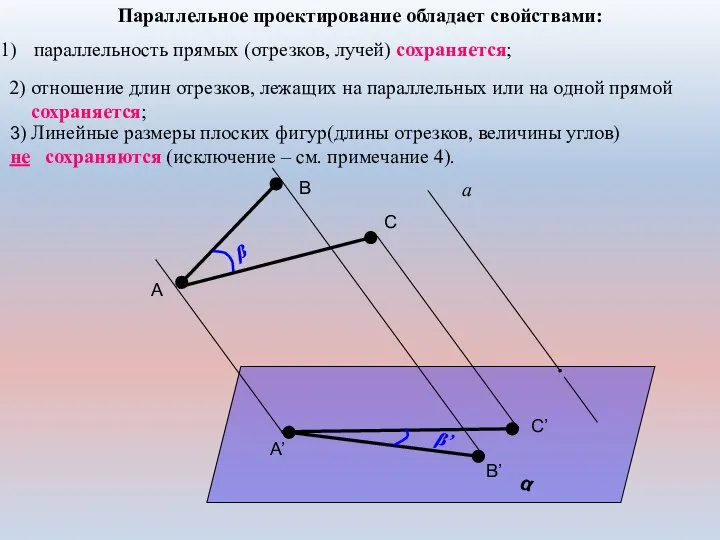
Параллельное проектирование обладает свойствами:
параллельность прямых (отрезков, лучей) сохраняется;
α
а
A
B
A’
B’
3) Линейные размеры плоских фигур(длины отрезков, величины углов) не сохраняются (исключение – см. примечание 4).
2) отношение длин отрезков, лежащих на параллельных или на одной прямой сохраняется;
β
β’
C
C’

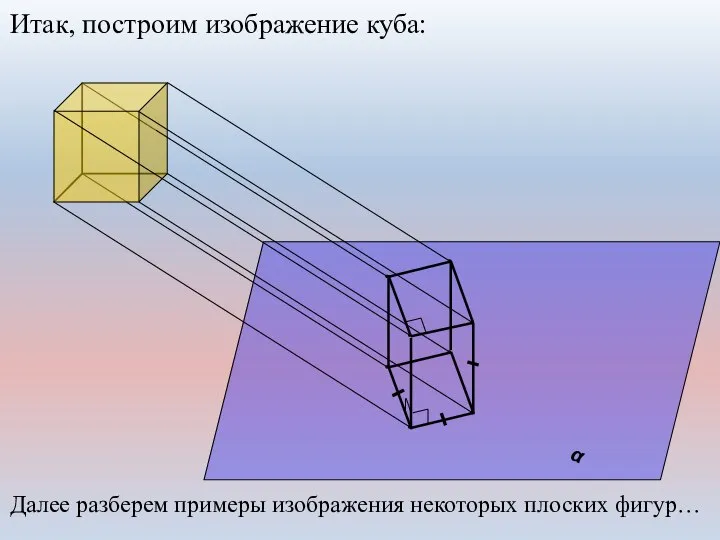
α
Итак, построим изображение куба:
Далее разберем примеры изображения некоторых плоских фигур…

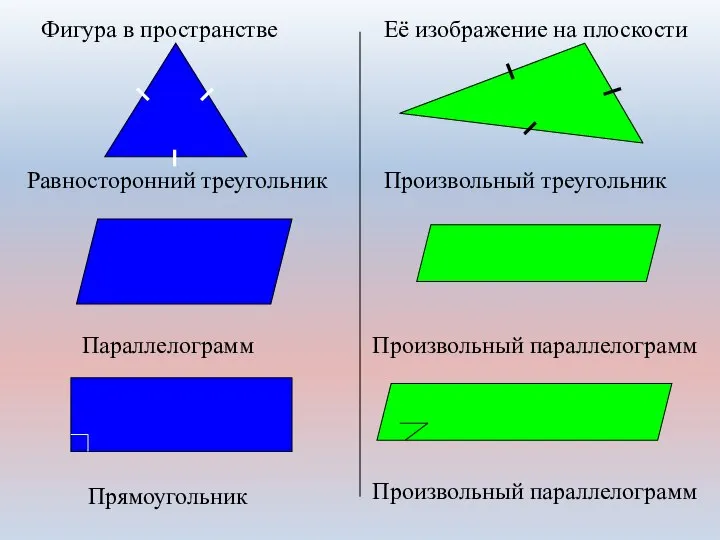
Фигура в пространстве
Её изображение на плоскости
Произвольный треугольник
Произвольный треугольник
Прямоугольный треугольник
Произвольный треугольник
Равнобедренный треугольник
Произвольный треугольник

Фигура в пространстве
Её изображение на плоскости
Равносторонний треугольник
Произвольный треугольник
Параллелограмм
Произвольный параллелограмм
Прямоугольник
Произвольный параллелограмм

Фигура в пространстве
Её изображение на плоскости
Квадрат
Произвольный параллелограмм
Трапеция
Произвольная трапеция
Произвольный параллелограмм
Ромб

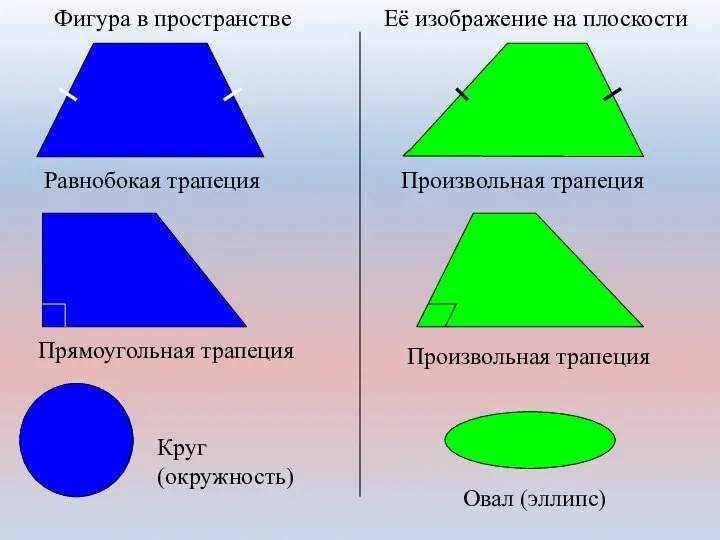
Фигура в пространстве
Её изображение на плоскости
Равнобокая трапеция
Произвольная трапеция
Прямоугольная трапеция
Произвольная трапеция
Круг (окружность)
Овал (эллипс)

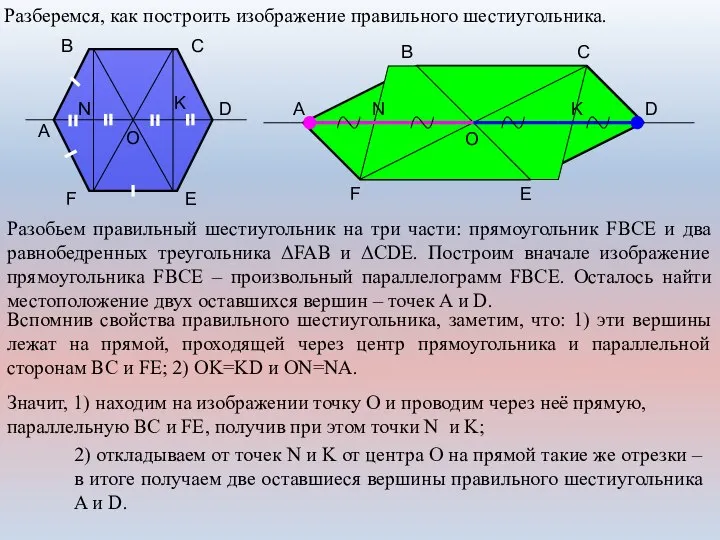
A
B
C
D
E
F
O
Разберемся, как построить изображение правильного шестиугольника.
F
A
B
C
D
E
Разобьем правильный шестиугольник на три части: прямоугольник FBCE и два равнобедренных треугольника ΔFAB и ΔCDE. Построим вначале изображение прямоугольника FBCE – произвольный параллелограмм FBCE. Осталось найти местоположение двух оставшихся вершин – точек A и D.
Вспомнив свойства правильного шестиугольника, заметим, что: 1) эти вершины лежат на прямой, проходящей через центр прямоугольника и параллельной сторонам BC и FE; 2) OK=KD и ON=NA.
K
N
Значит, 1) находим на изображении точку О и проводим через неё прямую, параллельную BC и FE, получив при этом точки N и K;
O
N
K
2) откладываем от точек N и K от центра О на прямой такие же отрезки – в итоге получаем две оставшиеся вершины правильного шестиугольника A и D.