Содержание
- 2. На сьогодні область питань чисельної побудови і неасимптотичної теорії чебишовських наближень привернула до себе увагу багатьох
- 3. Мета дослідження - розкрити цілісні методи ефективного чебишівського наближення і властивості розв’язань одномірної чебишовської задачі з
- 4. Об’єкт дослідження – навчальний процес з математики у закладах вищої освіти.
- 5. Предмет дослідження – методи і способи розв’язання одновимірної задачі Чебишевського.
- 6. Завдання дослідження: Зробити аналіз науково-методичної літератури з питань розв’язання одновимірної задачі чебишовського наближення поліномами. 2. Узагальнити
- 7. Явний вираз самого полінома лагранжевської інтерполяції з указаними вузлами Чебишева можна представити у вигляді:
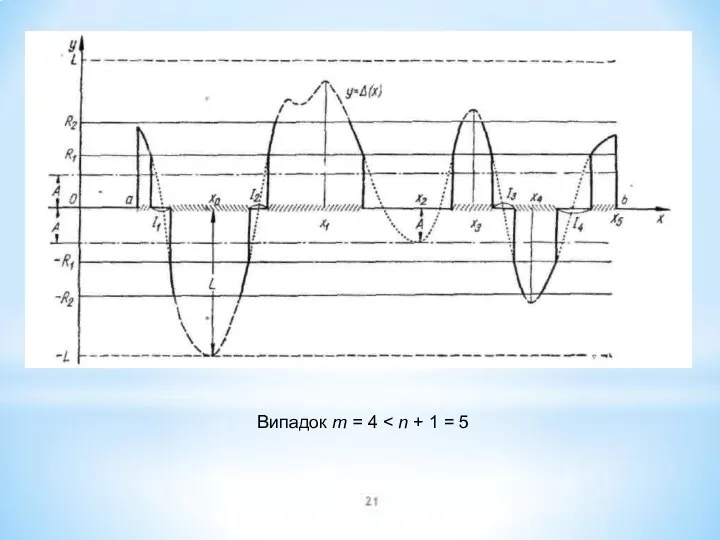
- 8. Випадок т = 4
- 9. 1. Попередні зауваження до прикладу f(x) = |х|, S = [- 1,1]. 2. Випадок n =
- 10. Лекція на тему: «Застосування поліноміальної інтерполяції та апроксимації для розв’язання задачі Чебишовського» Мета лекції: показати застосування
- 11. Властивості поліномів Чебишовського: Рекурентне співвідношення. Старший коефіцієнт. Симетрія. Тригонометричний запис на проміжку [-1;1]. Екстремуми.
- 12. Отже, для –1 Многочлени Чебишова широко використовуються при апроксимації функцій. Наближаючий поліном Чебишова Pn(x) степені Коефіцієнти
- 13. ВИСНОВКИ 1. У результаті дослідження розкриті цілісні методи ефективного чебишовського наближення і властивості розв’язань одномірної його
- 15. Скачать презентацию






![1. Попередні зауваження до прикладу f(x) = |х|, S = [- 1,1].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1064517/slide-8.jpg)

![Властивості поліномів Чебишовського: Рекурентне співвідношення. Старший коефіцієнт. Симетрія. Тригонометричний запис на проміжку [-1;1]. Екстремуми.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1064517/slide-10.jpg)


 Множества и операции над ними. Пустое множество. Способы задания множеств. Подмножества данного множества
Множества и операции над ними. Пустое множество. Способы задания множеств. Подмножества данного множества Применение компьютерных технологий
Применение компьютерных технологий Формулы сложения
Формулы сложения Сложение и вычитание векторов
Сложение и вычитание векторов Проценты. Три задачи
Проценты. Три задачи Обратные тригонометрические функции, их графики и формулы
Обратные тригонометрические функции, их графики и формулы Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного
Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного Презентация на тему Треугольники
Презентация на тему Треугольники  جدول داده-ستانده منطقهای
جدول داده-ستانده منطقهای Содержание кривых участков пути. Переходные кривые
Содержание кривых участков пути. Переходные кривые Тригонометрические и Логарифмические уравнения. Объёмы тел
Тригонометрические и Логарифмические уравнения. Объёмы тел Виды углов
Виды углов Опрос общественного мнения. Повторение действий с дробями
Опрос общественного мнения. Повторение действий с дробями Полуправильные многогранники
Полуправильные многогранники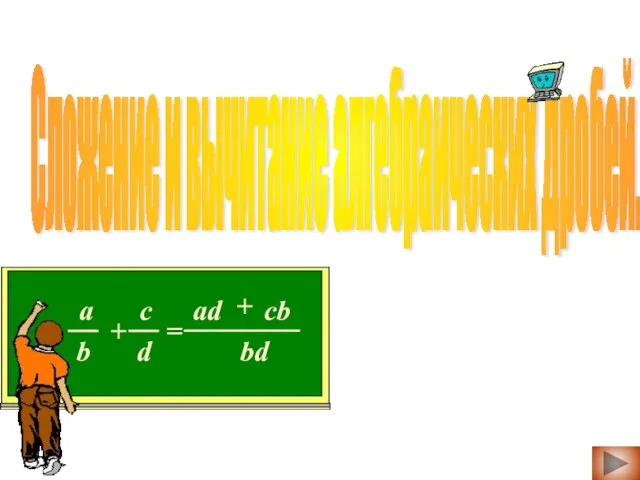 Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Решение треугольников
Решение треугольников Занимательная математика. 2 класс
Занимательная математика. 2 класс L(q(x), h, H) шекаралық есептің меншікті мәндері және A(A) характеристикалық функцияның нөлдері
L(q(x), h, H) шекаралық есептің меншікті мәндері және A(A) характеристикалық функцияның нөлдері Первый признак равенства треугольников
Первый признак равенства треугольников Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Человек и число
Человек и число Нумерационные случаи сложения и вычитания чисел второго десятка
Нумерационные случаи сложения и вычитания чисел второго десятка Сечение многогранника плоскостью
Сечение многогранника плоскостью Решение задач. Параллелограмм. (9 класс. Геометрия)
Решение задач. Параллелограмм. (9 класс. Геометрия) Равнобедренный треугольник. Свойства равнобедренного треугольника
Равнобедренный треугольник. Свойства равнобедренного треугольника Понятие многогранника, призмы и их элементов
Понятие многогранника, призмы и их элементов Вывод формулы длины окружности и площади круга
Вывод формулы длины окружности и площади круга Математический расчёт параметров секций однополостных гиперболоидов
Математический расчёт параметров секций однополостных гиперболоидов