Основные положения теории групп

ВОПРОСЫ ЛЕКЦИИ
Определение группы симметрии
Условия существования группы
Теоремы о взаимодействии элементов симметрии

ОПРЕДЕЛЕНИЕ ГРУППЫ СИММЕТРИИ
Рассмотренные симметрические преобразования в реальных кристаллах встречаются в виде определенных совокупностей – групп.
Поэтому при разработке теории симметрии кристаллов использовали раздел математической теории абстрактных групп.
Группой называется множество объектов G любой природы с заданной бинарной операцией *, если для любой пары элементов a и b этого множества G определен третий, результирующий элемент c=a*b того же множества. В общем случае a*b≠b*a.
Группа (класс) симметрии кристалла – это совокупность всех различных неэквивалентных симметрических операций – сочетаний элементов симметрии, преобразующих фигуру саму в себя.
При том их взаимные расположения подчиняются всем положениям математической теории абстрактных групп. В общем случае результирующие операции могут оказаться различными, если поменять порядок выполнения исходных операций.

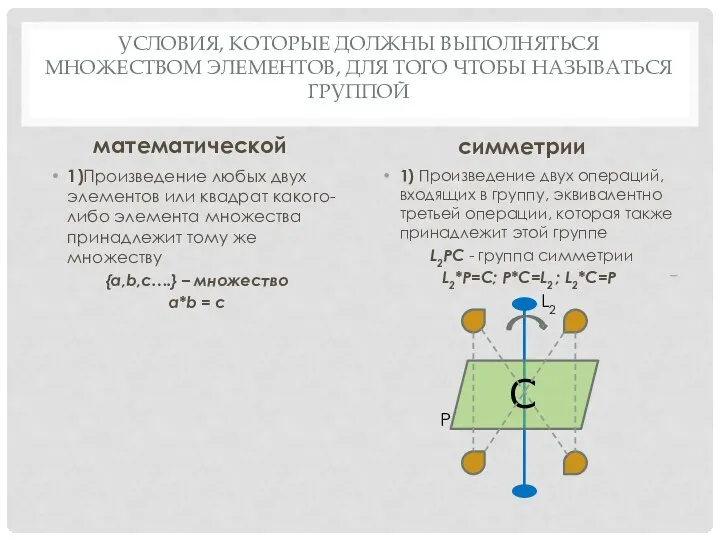
УСЛОВИЯ, КОТОРЫЕ ДОЛЖНЫ ВЫПОЛНЯТЬСЯ МНОЖЕСТВОМ ЭЛЕМЕНТОВ, ДЛЯ ТОГО ЧТОБЫ НАЗЫВАТЬСЯ
ГРУППОЙ
математической
1)Произведение любых двух элементов или квадрат какого-либо элемента множества принадлежит тому же множеству
{a,b,c….} – множество
a*b = c
симметрии
1) Произведение двух операций, входящих в группу, эквивалентно третьей операции, которая также принадлежит этой группе
L2PC - группа симметрии
L2*P=C; P*C=L2 ; L2*C=P
L2
P
C

УСЛОВИЯ, КОТОРЫЕ ДОЛЖНЫ ВЫПОЛНЯТЬСЯ МНОЖЕСТВОМ ЭЛЕМЕНТОВ, ДЛЯ ТОГО ЧТОБЫ НАЗЫВАТЬСЯ
ГРУППОЙ
математической
2) Для любых трех элементов множества выполняется ассоциативный (сочетательный) закон
(a*b)*c=a*(b*c)
3) Существование единичного члена e – такого единичного члена, что для любого элемента группы будет выполняться равенство
e*a=a*e
симметрии
2) Произведение трех любых симметрических операций в общем случае удовлетворяет ассоциативной операции
(L2*P)*C= L2*(P*C)
3) Произведение операций отождествления (действие оси первого порядка – поворот на 360°) на любой элемент группы эквивалентно обратному произведению
L1*P=P*L1

УСЛОВИЯ, КОТОРЫЕ ДОЛЖНЫ ВЫПОЛНЯТЬСЯ МНОЖЕСТВОМ ЭЛЕМЕНТОВ, ДЛЯ ТОГО ЧТОБЫ НАЗЫВАТЬСЯ
ГРУППОЙ
математической
4) Обратимость - для любого элемента a существует элемент a-1 из того же множества, называемый обратным элементом к элементу a, такой, что
a*a-1 = a-1*a =e
Множество элементов составляет математическую группу, если оно удовлетворяет всем 4 условиям
симметрии
4) Каждому элементу группы соответствует обратный элемент.
Если α – правый поворот вокруг оси симметрии на угол 360°/n, то α-1 – такой же левый поворот, равный
(360°-360°/n).
Сумма правого и левого поворотов эквивалентна полному повороту вокруг L1, т.е. 360°.
Симметрические преобразования I и II рода составляют группу симметрии если удовлетворяют всем 4 условиям

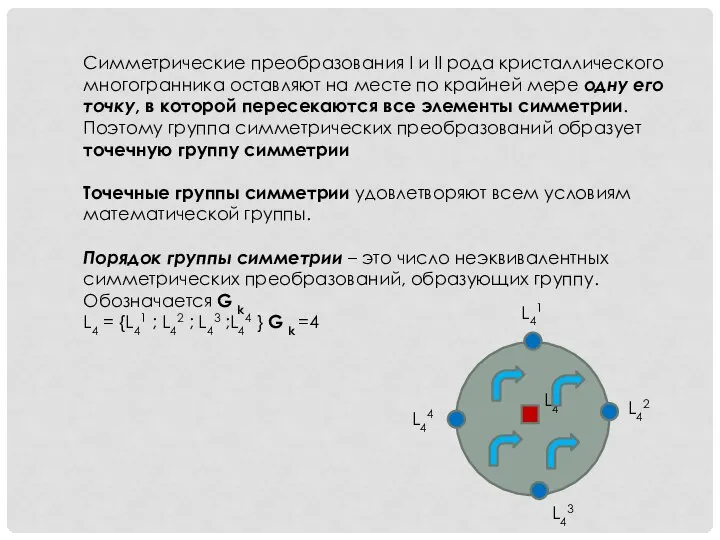
Симметрические преобразования I и II рода кристаллического многогранника оставляют на месте по крайней мере одну его точку, в которой пересекаются все элементы симметрии. Поэтому группа симметрических преобразований образует точечную группу симметрии
Точечные группы симметрии удовлетворяют всем условиям математической группы.
Порядок группы симметрии – это число неэквивалентных симметрических преобразований, образующих группу. Обозначается G k
L4 = {L41 ; L42 ; L43 ;L44 } G k =4
L41
L42
L43
L44
L4

ТЕОРЕМЫ О ВЗАИМОДЕЙСТВИИ ЭЛЕМЕНТОВ СИММЕТРИИ

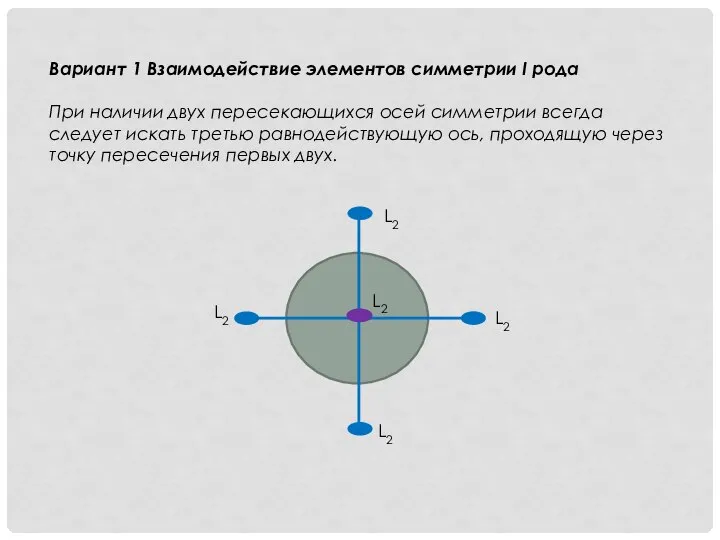
Вариант 1 Взаимодействие элементов симметрии I рода
При наличии двух пересекающихся осей симметрии всегда следует искать третью равнодействующую ось, проходящую через точку пересечения первых двух.

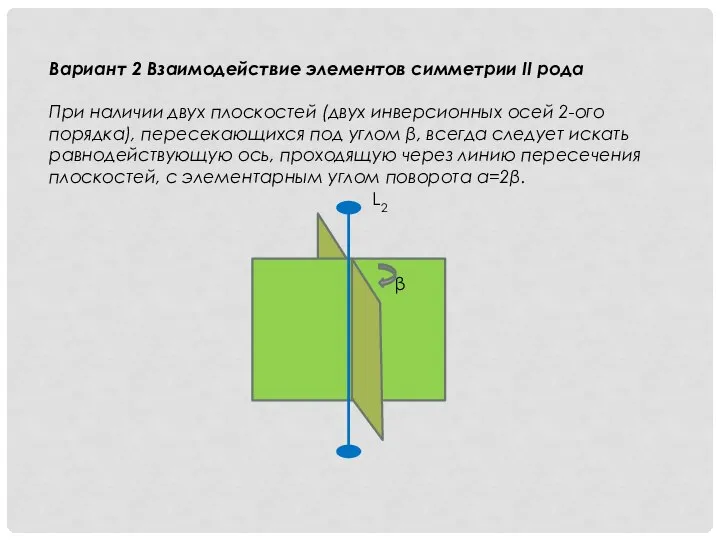
Вариант 2 Взаимодействие элементов симметрии II рода
При наличии двух плоскостей (двух инверсионных осей 2-ого порядка), пересекающихся под углом β, всегда следует искать
равнодействующую ось, проходящую через линию пересечения плоскостей, с элементарным углом поворота α=2β.
β

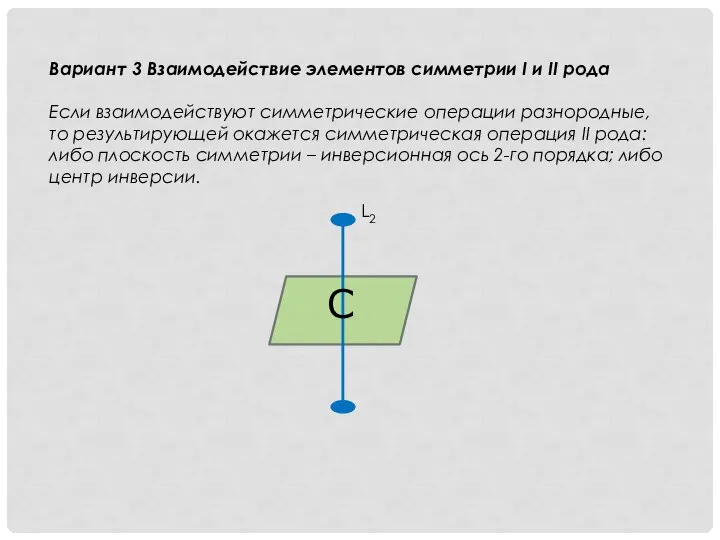
Вариант 3 Взаимодействие элементов симметрии I и II рода
Если взаимодействуют симметрические операции разнородные, то результирующей окажется симметрическая операция II рода: либо плоскость симметрии – инверсионная ось 2-го порядка; либо центр инверсии.

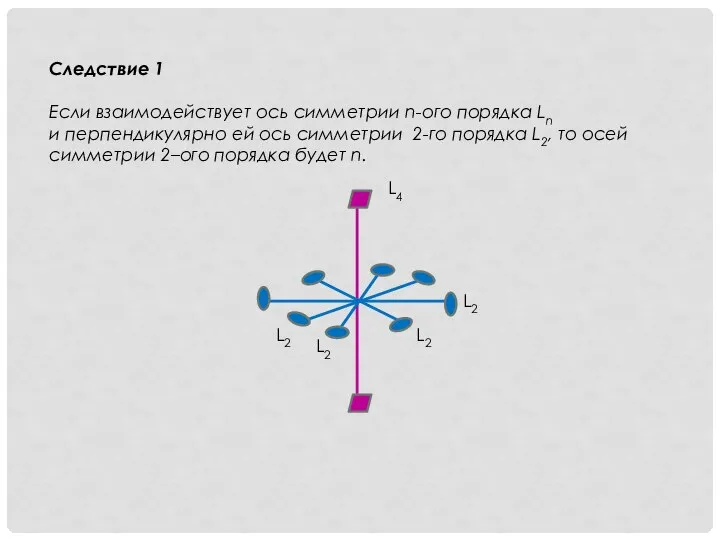
Следствие 1
Если взаимодействует ось симметрии n-ого порядка Ln
и перпендикулярно ей ось симметрии 2-го порядка L2, то осей симметрии 2–ого порядка будет n.
L2
L2
L2
L2
L4