Слайд 2I. СВЕДЕНИЕ К АЛГЕБРАИЧЕСКОМУ.

Слайд 3Пример:
Пусть .
Уравнение примет вид:
- не удовлетворяет условию
Ответ: .

Слайд 4II. ОДНОРОДНЫЕ И СВОДИМЫЕ К НИМ.

Слайд 5 Уравнение вида
называется однородным уравнением I степени.

Слайд 6 Пример:
Множество значений x, удовлетворяющих уравнению
, не является решением данного уравнения.

Поэтому можно обе части уравнения разделить на .
Получим:
Ответ: .
Слайд 7 Уравнение вида
называется однородным уравнением II степени.

Слайд 8Пример:
Решение:
Множество значений x, удовлетворяющих уравнению , не является решением данного уравнения.
Разделим обе

части уравнения на .
Получим:
Слайд 9Пусть .
Уравнение примет вид:
Ответ:

Слайд 10III. ЕСЛИ В УРАВНЕНИИ СОДЕРЖИТСЯ ПРОИЗВЕДЕНИЕ ФУНКЦИЙ SIN(АX)SIN(BX), SIN(AX)COS(BX), COS(AX)COS(BX), ТО ТАКИЕ

УРАВНЕНИЯ РЕШАЮТСЯ ПРЕОБРАЗОВАНИЕМ ПРОИЗВЕДЕНИЯ В СУММУ (РАЗНОСТЬ) И НАОБОРОТ.
Слайд 15Если в уравнении содержатся чётные степени sinx и cosx, то понижают степень

уравнения с применением формул понижения степени:
Слайд 19VI. ВВЕДЕНИЕ ВСПОМОГАТЕЛЬНОГО АРГУМЕНТА.

Слайд 20Пример
Решение:
Разделим обе части уравнения на
Получаем:
Ответ:

Слайд 21VII. ПРИМЕНЕНИЕ УНИВЕРСАЛЬНОЙ ПОДСТАНОВКИ.

Слайд 23Пример
Решение:
Пусть: . Уравнение примет вид . О.Д.З. .
не удовлетворяет условию
Ответ: ;

.
Слайд 24Пример 2:
Решение:
Проверка:
Ответ: ; .

Слайд 25VIII. ВВЕДЕНИЕ НОВОГО ПЕРЕМЕННОГО.

Слайд 26! Если в уравнении содержится сумма или разность sinx и cosx и

их произведения, то уравнение решается введением нового переменного:
Слайд 27Пример:
Пусть:
(Решите самостоятельно)
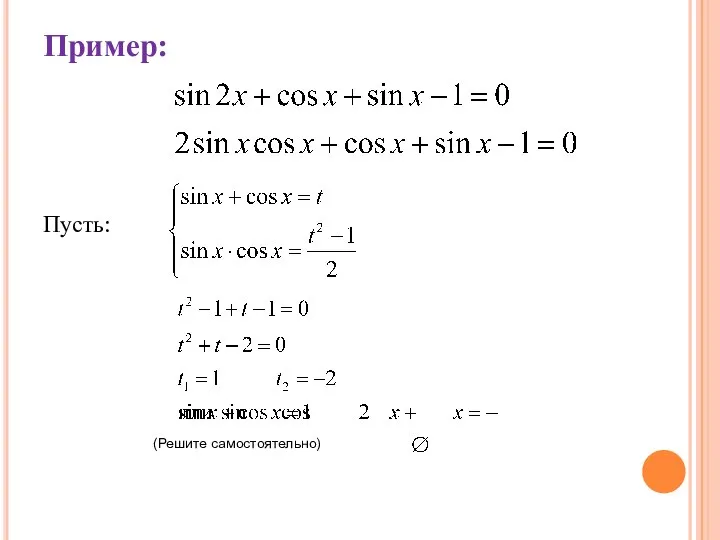
Слайд 28IX. ИСПОЛЬЗОВАНИЕ ПОНЯТИЯ ОГРАНИЧЕННОСТИ (МИНИМАКС).











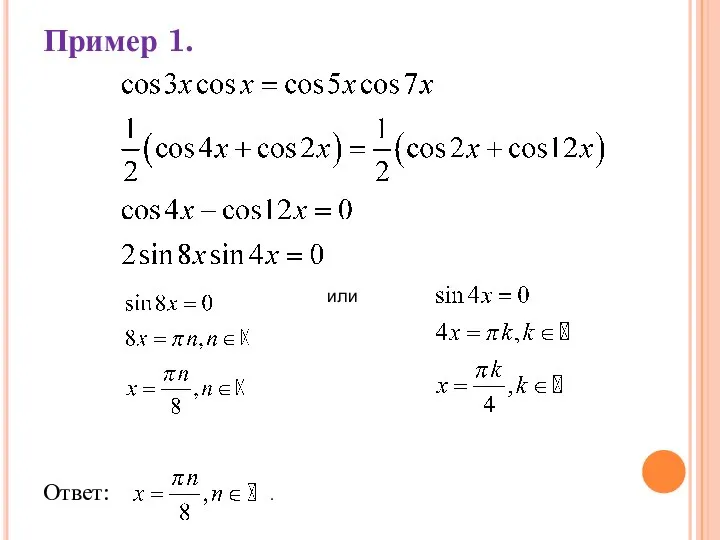



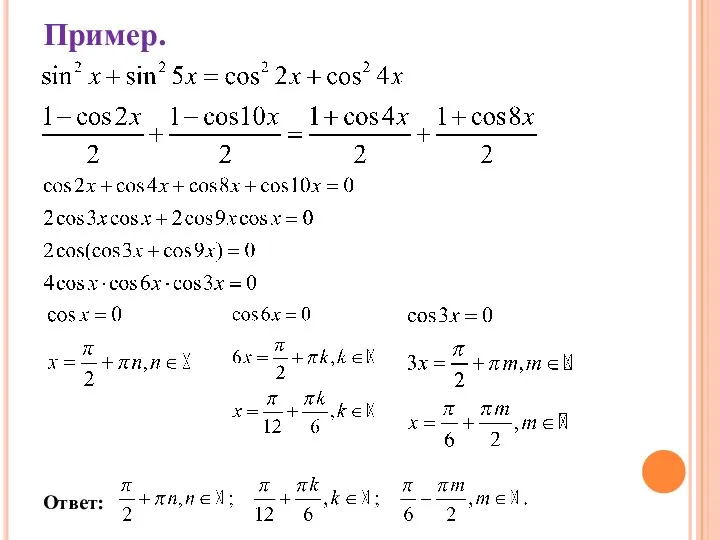









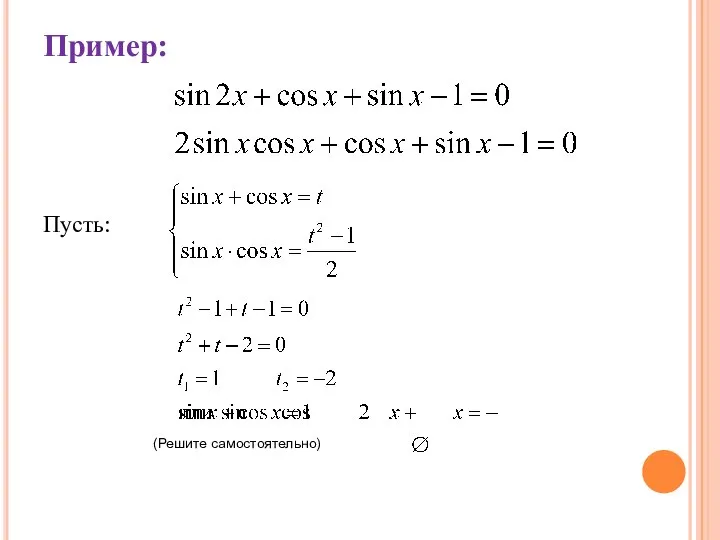

 Десятичные дроби
Десятичные дроби Преобразование формул
Преобразование формул Презентация на тему Великие русские математики
Презентация на тему Великие русские математики  Иррациональные уравнения
Иррациональные уравнения Угол
Угол Колесо истории математики
Колесо истории математики Интерактивный тренажёр. 4 класс
Интерактивный тренажёр. 4 класс Средняя линия треугольника
Средняя линия треугольника Приёмы устных вычислений
Приёмы устных вычислений Численные методы решения СЛАУ (часть 1)
Численные методы решения СЛАУ (часть 1) Преобразование графиков функции
Преобразование графиков функции Коэффициент. Числовой коэффициент
Коэффициент. Числовой коэффициент Выборочное наблюдение. Практическое занятие
Выборочное наблюдение. Практическое занятие Задания ГИА на нахождение площадей фигур, на выбор правильного утверждения
Задания ГИА на нахождение площадей фигур, на выбор правильного утверждения Основы моделирования
Основы моделирования Угол между прямой и плоскостью (Задание 13)
Угол между прямой и плоскостью (Задание 13) Устная работа на уроке геометрии
Устная работа на уроке геометрии Пифагор и его школа
Пифагор и его школа Методы общения линейных уравнений с тремя неизвестными
Методы общения линейных уравнений с тремя неизвестными Сечение многогранников. Применение интерактивных методов обучения на уроках математики
Сечение многогранников. Применение интерактивных методов обучения на уроках математики Анимированный плакат. Цифры-прописи
Анимированный плакат. Цифры-прописи Временные ряды
Временные ряды Методика проверки и оценки алгебраических заданий повышенного уровня сложности
Методика проверки и оценки алгебраических заданий повышенного уровня сложности Дифференциальные уравнения
Дифференциальные уравнения Эндогенность. Инструментальные переменные
Эндогенность. Инструментальные переменные Векторы. Нулевой вектор
Векторы. Нулевой вектор Линейная алгебра и аналитическая геометрия
Линейная алгебра и аналитическая геометрия Цилиндр. История возникновения
Цилиндр. История возникновения