Содержание
- 2. Внимательно изучите и перепишите информацию со слайдов 3-6. Особое внимание уделите разбору примеров 1-3. Дайте ответы
- 3. Комбинаторика – раздел математики, рассматривающий решение комбинаторных задач. Комбинаторные задачи – это теоретические и практические задачи,
- 4. РАЗМЕЩЕНИЯ Размещением из n элементов по m в каждом называют такие соединения , которые отличаются друг
- 5. ПЕРЕСТАНОВКИ Перестановками из n элементов называют соединения из всех n элементов, отличающиеся друг от друга только
- 6. СОЧЕТАНИЯ Сочетаниями из n элементов по m в каждом называют соединения, отличающиеся друг от друга хотя
- 8. Скачать презентацию





 Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ  Презентация на тему Математический диктант 2 класс
Презентация на тему Математический диктант 2 класс  Операции над множествами
Операции над множествами Применение интегральной технологии при изучении алгебраических уравнений
Применение интегральной технологии при изучении алгебраических уравнений Проецирование на две плоскости проекций
Проецирование на две плоскости проекций Золотое сечение в архитектуре
Золотое сечение в архитектуре Арифметический квадратный корень
Арифметический квадратный корень Решение задачи Корабли или история 7 семестров
Решение задачи Корабли или история 7 семестров Backpropagation
Backpropagation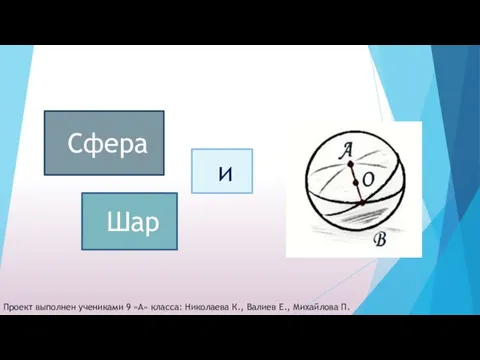 Сфера и шар
Сфера и шар Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы Перпендикулярность плоскостей
Перпендикулярность плоскостей Биометрия, как наука
Биометрия, как наука Множества. Решение задач
Множества. Решение задач Презентация на тему Симметрия и движение (9 класс)
Презентация на тему Симметрия и движение (9 класс)  Египетский треугольник
Египетский треугольник Координатная плоскость. Ордината. Абсцисса
Координатная плоскость. Ордината. Абсцисса Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника Введение в комбинаторику. 7 класс
Введение в комбинаторику. 7 класс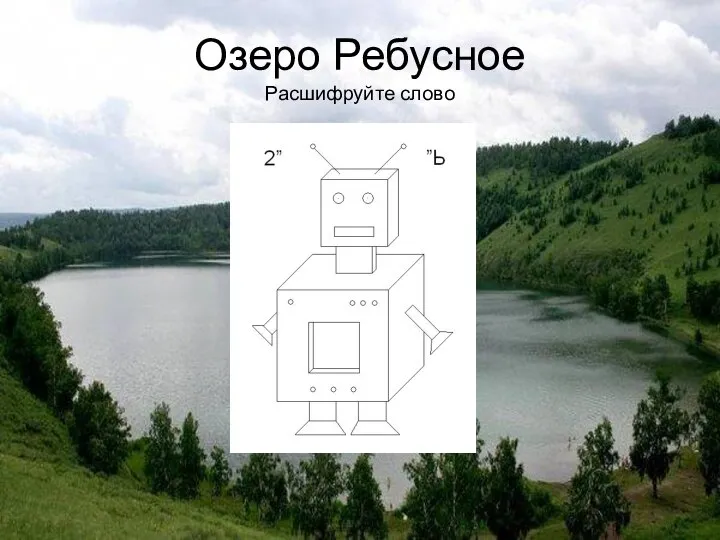 Расшифруйте слово
Расшифруйте слово Формулы сложения. 10 класс
Формулы сложения. 10 класс Дискретная математика
Дискретная математика Круги Эйлера в решении задач
Круги Эйлера в решении задач Комбинаторика. Перебор вариантов. Решение задач
Комбинаторика. Перебор вариантов. Решение задач Признаки параллельности прямых
Признаки параллельности прямых Правила вычисления производных
Правила вычисления производных Правильные многогранники
Правильные многогранники Тригонометрические функции y = tg x и y = ctg x, их свойства и графики
Тригонометрические функции y = tg x и y = ctg x, их свойства и графики