Содержание
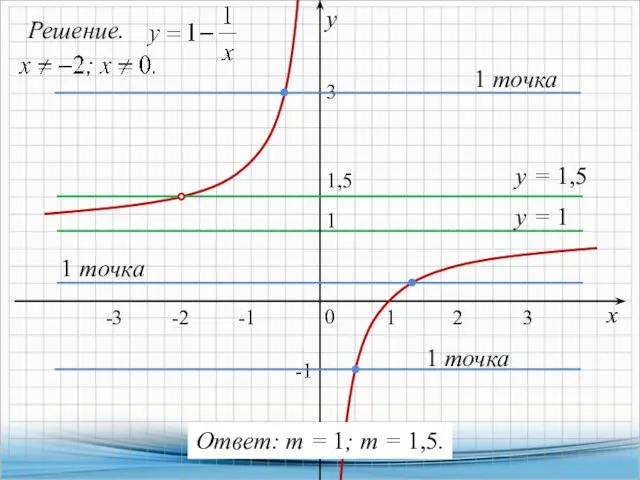
- 2. 1. Постройте график функции и определите, при каких значениях т прямая у = т не имеет
- 3. Решение. х у 0 1 1 -2 у = 1 у = 1,5 1,5 -1 -1
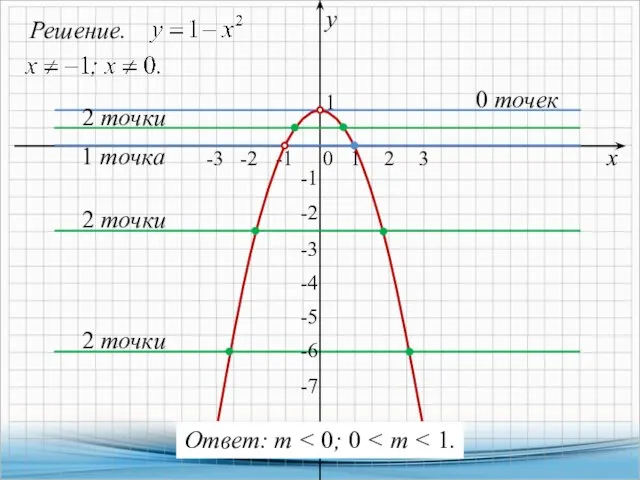
- 4. 2. Постройте график функции и определите, при каких значениях т прямая у = т имеет с
- 5. Решение. х у 0 1 1 -2 2 точки 2 точки -1 -1 2 -3 3
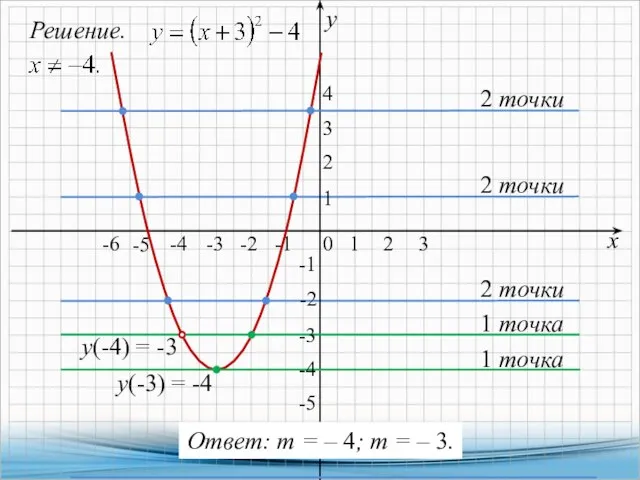
- 6. 3. Постройте график функции и определите, при каких значениях т прямая у = т имеет с
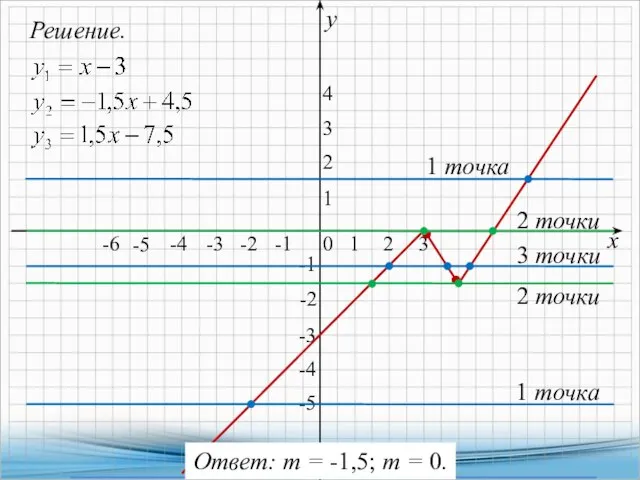
- 7. Решение. х у 0 1 1 -2 1 точка -1 -1 2 -3 3 -5 2
- 8. 4. Постройте график функции Какое наибольшее число общих точек график данной функции может иметь с прямой,
- 9. Решение. х у 0 1 1 -2 4 точки -1 -1 2 -3 3 -5 2
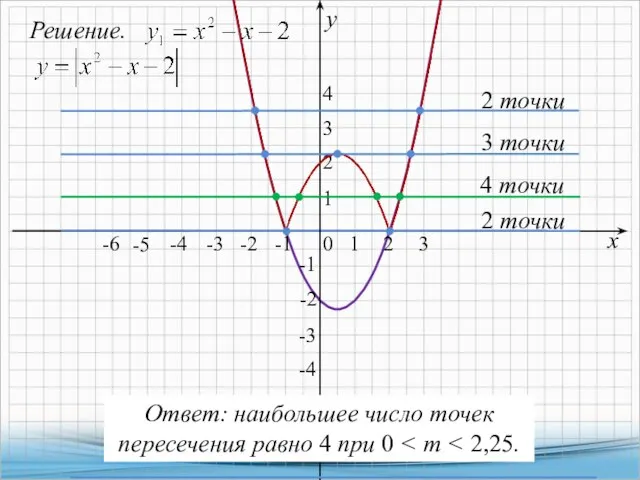
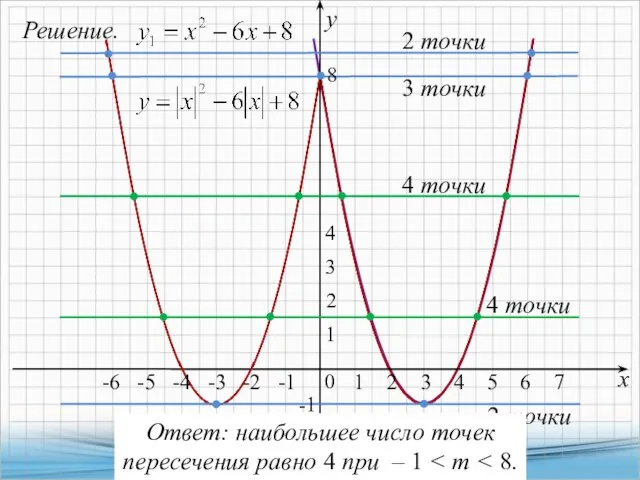
- 10. 5. Постройте график функции Какое наибольшее число общих точек график данной функции может иметь с прямой,
- 11. Решение. х у 4 точки -2 2 точки Ответ: наибольшее число точек пересечения равно 4 при
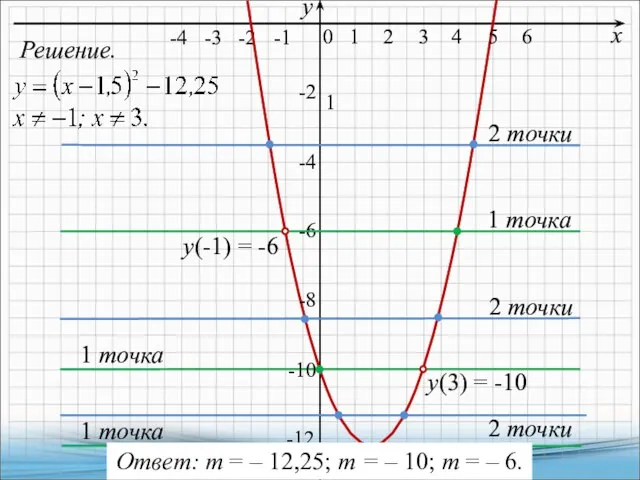
- 12. 6. Постройте график функции и определите, при каких значениях т прямая у = т имеет с
- 13. Решение. х у 0 1 1 -2 1 точка -1 -4 2 -3 3 -6 -2
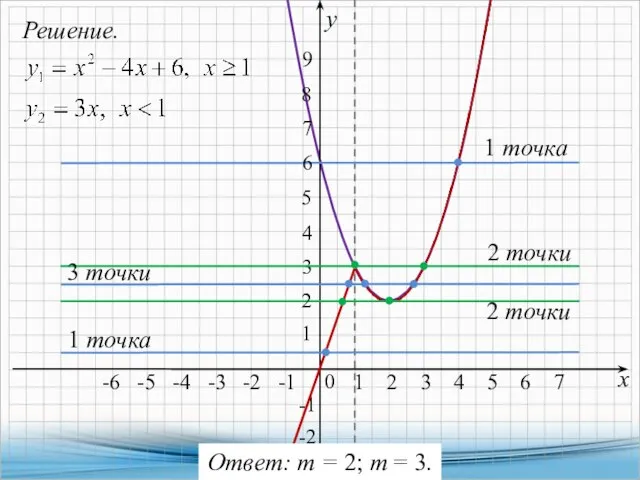
- 14. 7. Постройте график функции и определите, при каких значениях т прямая у = т имеет с
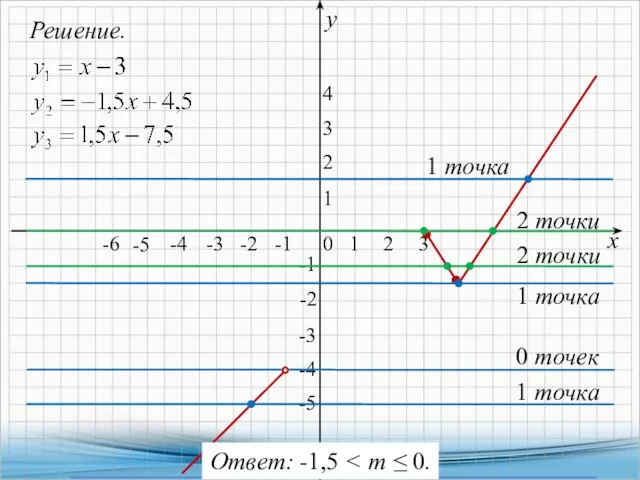
- 15. Решение. х у 2 точки -2 1 точка -6 -5 -4 -3 -2 -1 2 3
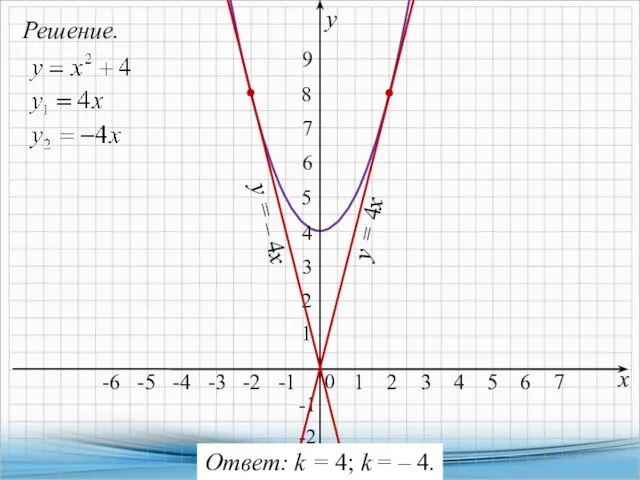
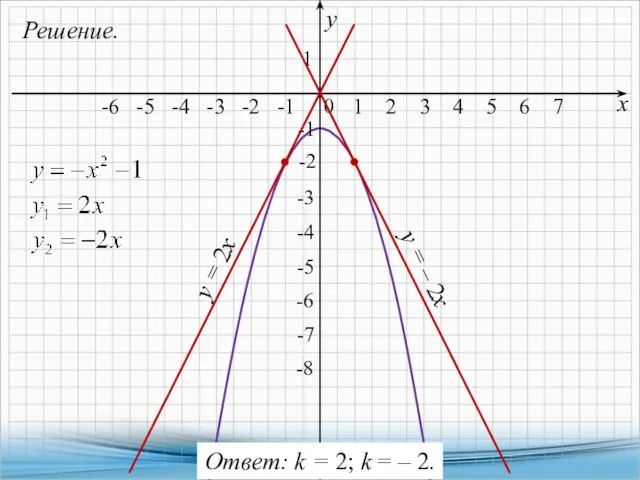
- 16. 8. Найдите все значения k, при каждом из которых прямая y = kx имеет с графиком
- 17. Решение. х у -2 -6 -5 -4 -3 -2 -1 2 3 4 1 2 3
- 18. 9. Найдите все значения k, при каждом из которых прямая y = kx имеет с графиком
- 19. Решение. х у -2 -6 -5 -4 -3 -2 -1 -6 -5 -4 1 2 3
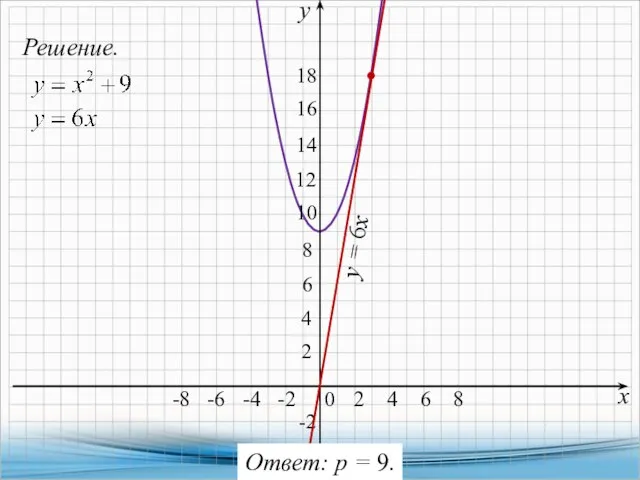
- 20. 10. Найдите p и постройте график функции y = x2 + p если известно, что прямая
- 21. Решение. х у -4 -8 -6 -4 -2 4 6 8 2 4 6 8 2
- 22. 11. Постройте график функции и определите, при каких значениях т прямая у = т не имеет
- 23. Решение. х у -2 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6
- 24. 12. Постройте график функции и определите, при каких значениях т прямая у = т не имеет
- 25. Решение. х у -2 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6
- 26. 13. Постройте график функции и определите, при каких значениях т прямая у = т имеет с
- 27. Решение. х у 2 точки -2 -6 -5 -4 -3 -2 -1 2 3 4 1
- 28. 14. Постройте график функции и определите, при каких значениях т прямая у = т имеет с
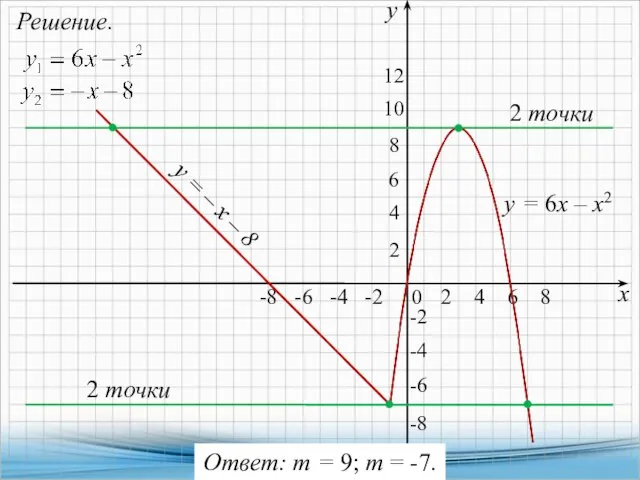
- 29. Решение. х у -4 -8 -6 -4 -2 -2 -6 2 -4 0 -8 4 6
- 30. 15. Постройте график функции и определите, при каких значениях k прямая у = kx имеет с
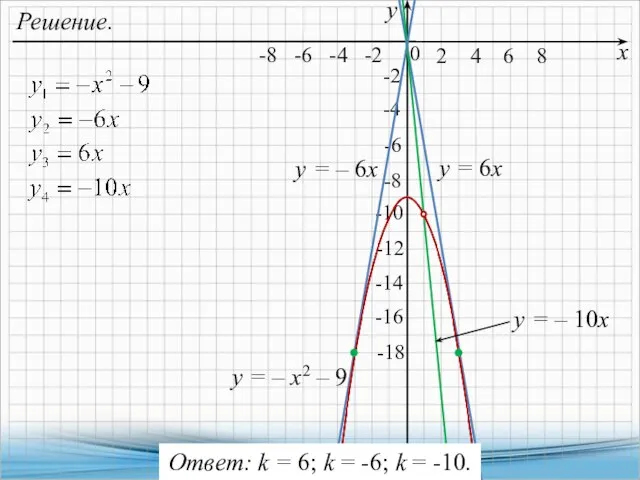
- 31. Решение. Другими словами, нужно найти все значения k, при каждом из которых система имеет одно решение:
- 32. Решение. х у -8 -6 -4 -2 -14 -12 0 -10 -8 -6 -4 -2 y
- 33. 16.1. Постройте график функции и определите, при каких значениях т прямая у = т имеет с
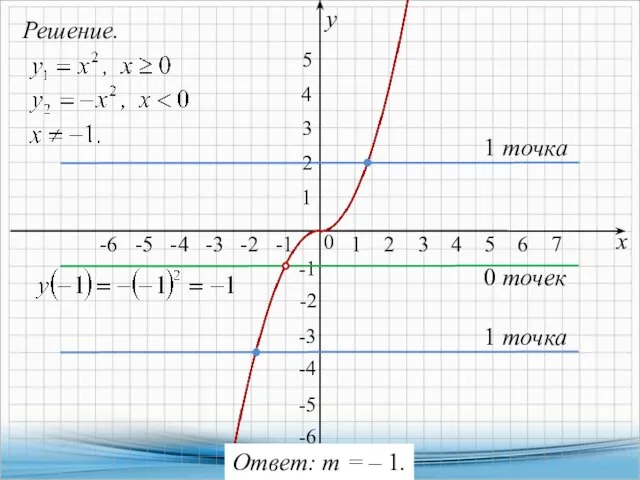
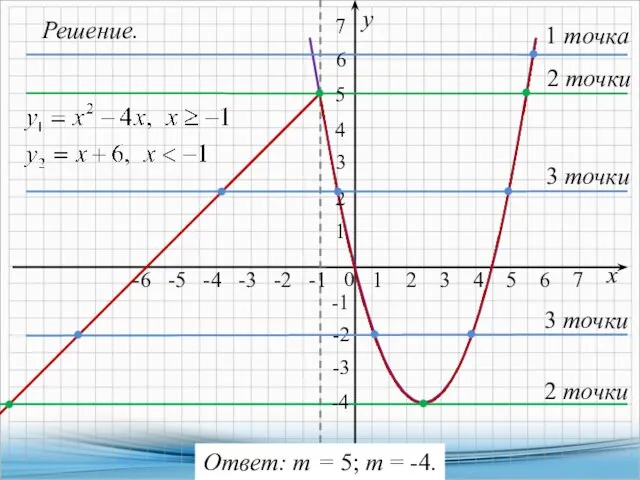
- 34. Решение. х у 0 1 1 -2 -1 -1 2 -3 3 -5 -4 -5 -6
- 35. 16.2. Постройте график функции и определите, при каких значениях т прямая у = т имеет с
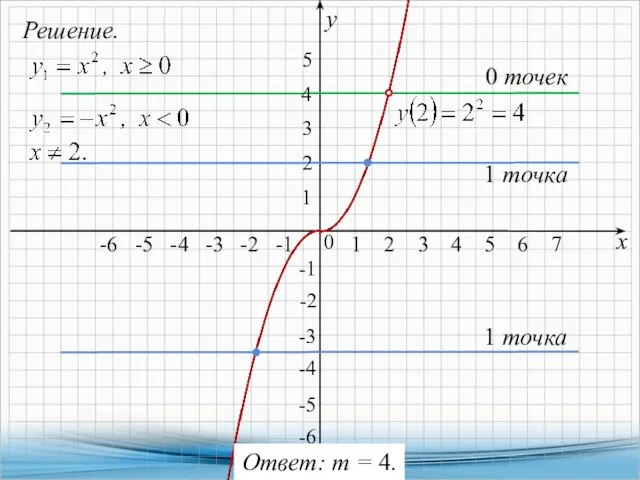
- 36. Решение. х у 0 1 1 -2 -1 -1 2 -3 3 -5 -4 -5 -6
- 38. Скачать презентацию


















 Геометрическая оптика. 11 класс. ЕГЭ
Геометрическая оптика. 11 класс. ЕГЭ Исторические сведения
Исторические сведения Комбинаторные методы решения вероятностных задач
Комбинаторные методы решения вероятностных задач Подготовка к ГИА. Демоверсия 2013
Подготовка к ГИА. Демоверсия 2013 Квадратный корень из степени
Квадратный корень из степени Проценты и десятичные дроби
Проценты и десятичные дроби Производные тригонометрических функций. 10 класс
Производные тригонометрических функций. 10 класс Задания из открытого банка ЕГЭ
Задания из открытого банка ЕГЭ Вероятность события 9 класс
Вероятность события 9 класс Пропорциональные отрезки в прямоугольном треугольнике (8 класс)
Пропорциональные отрезки в прямоугольном треугольнике (8 класс) Презентация на тему Угол вписанный в окружность
Презентация на тему Угол вписанный в окружность  Схема Горнера. Уильям Джордж Горнер
Схема Горнера. Уильям Джордж Горнер Двійкова арифметика
Двійкова арифметика Решение задач с помощью уравнений. Устные вычисления
Решение задач с помощью уравнений. Устные вычисления Число и цифра 7. Написание цифр 7. Сравнение чисел в пределах 7
Число и цифра 7. Написание цифр 7. Сравнение чисел в пределах 7 Область определения функции
Область определения функции Подборка заданий по геометрии за курс 7 класса
Подборка заданий по геометрии за курс 7 класса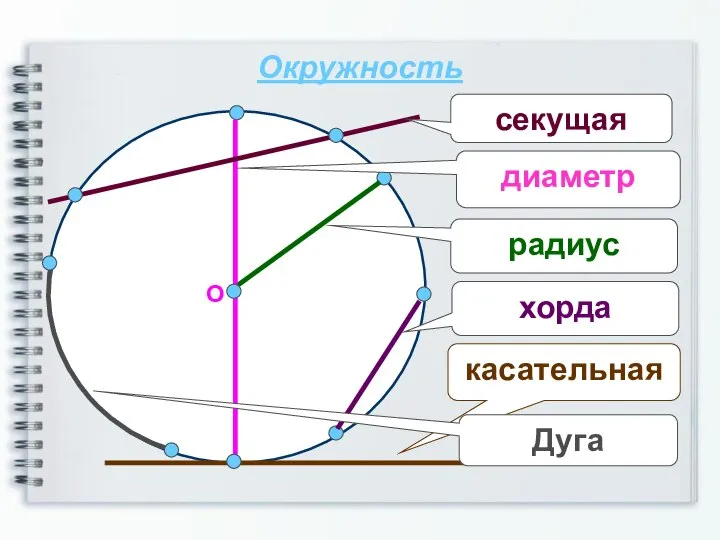 Д.з. на 16.09 Углы и отрезки, связанные с окружностью (1)
Д.з. на 16.09 Углы и отрезки, связанные с окружностью (1) Многочлен и его стандартный вид
Многочлен и его стандартный вид Системы линейных уравнений с двумя неизвестными
Системы линейных уравнений с двумя неизвестными Геометрия. Построение сечений
Геометрия. Построение сечений Сводка и группировка статистических данных
Сводка и группировка статистических данных Прикладная математика. Лекция 10. Контрольная работа
Прикладная математика. Лекция 10. Контрольная работа Зачем изучать математику?
Зачем изучать математику? Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Геометрические фигуры (круг)
Геометрические фигуры (круг) Решение задач с помощью уравнений. Алгебра. 7 класс. Ю.М. Колягин и др
Решение задач с помощью уравнений. Алгебра. 7 класс. Ю.М. Колягин и др Подготовка к контрольной работе. Изображение промежутков и запись их в виде неравенств
Подготовка к контрольной работе. Изображение промежутков и запись их в виде неравенств