Многоугольники

Многоуго́льником называется геометрическая фигура, состоящая из n
(n больше или равно 3) точек плоскости, не лежащих на одной прямой и попарно соединённых непересекающимися отрезками
Многоугольник-это замкнутая ломаная линия.

1
2
3
4
5
6
7
8
9
10
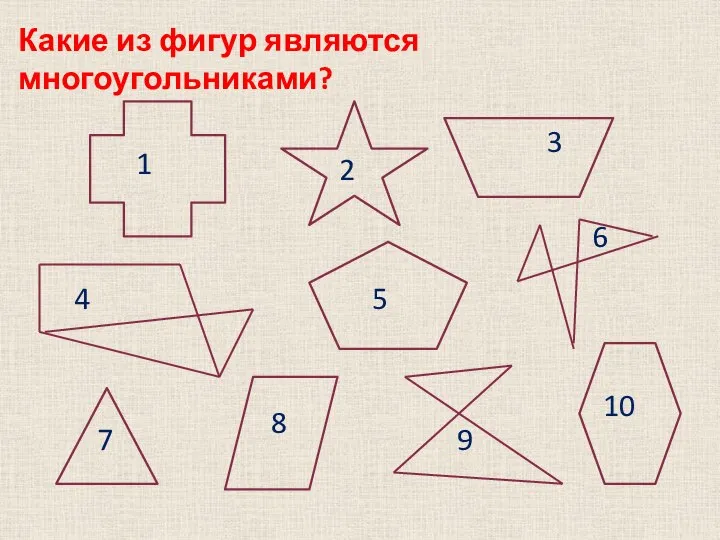
Какие из фигур являются многоугольниками?

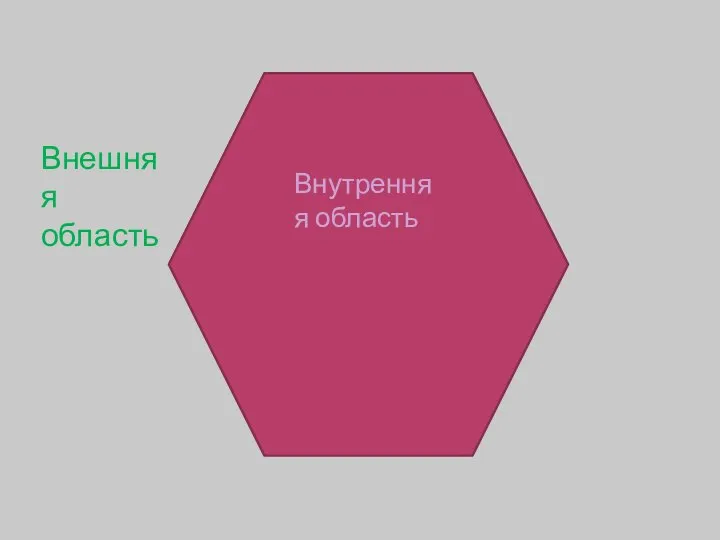
Внутренняя область
Внешняя область

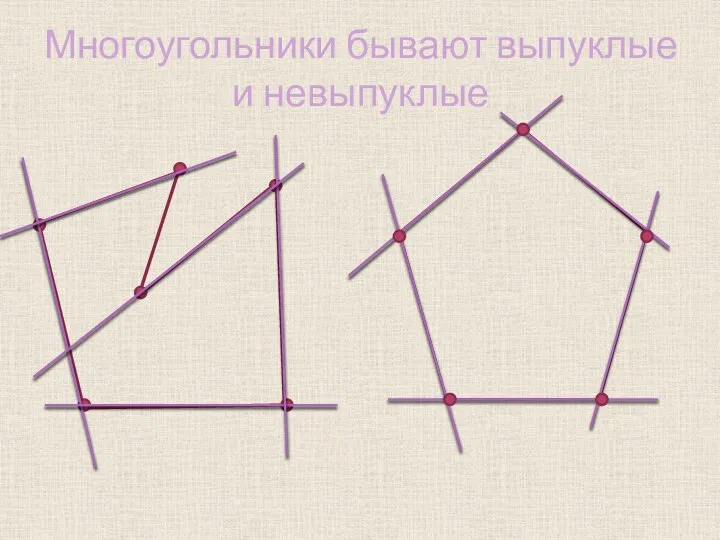
Чем отличаются эти многоугольники?

Многоугольники бывают выпуклые и невыпуклые

D
C
ABCDEFG -многоугольник
A, B, C, D, E, F, G – вершины этого многоугольника
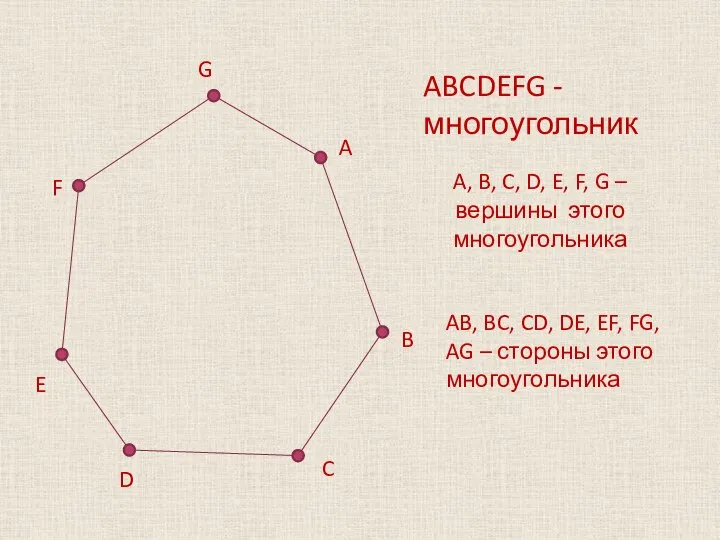
AB, BC, CD, DE, EF, FG, AG – стороны этого многоугольника

A
B
E
F
G
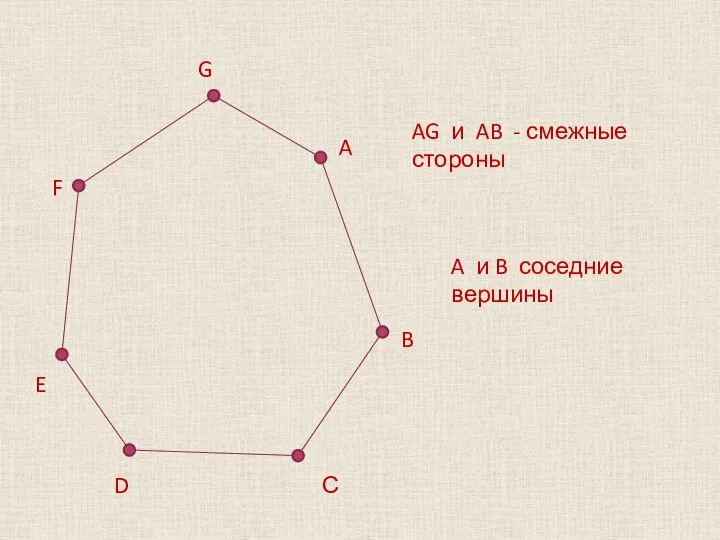
AG и AB - смежные стороны
A и B соседние вершины
С
D

A
B
E
F
G
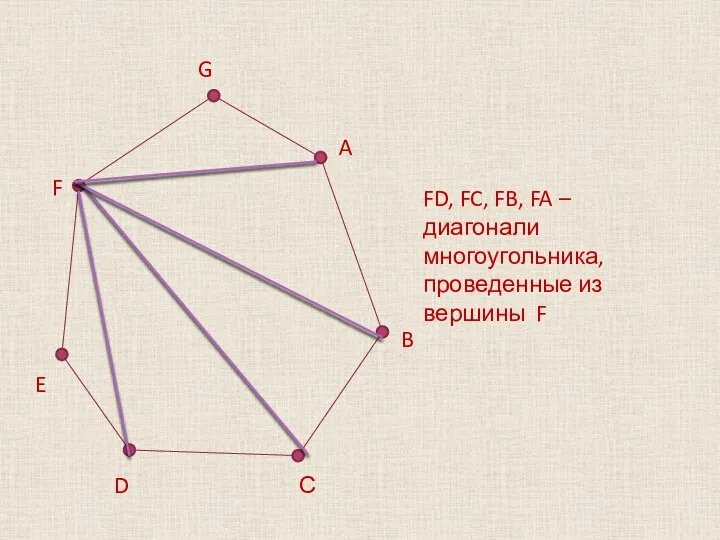
FD, FC, FB, FA – диагонали многоугольника, проведенные из вершины F
С
D

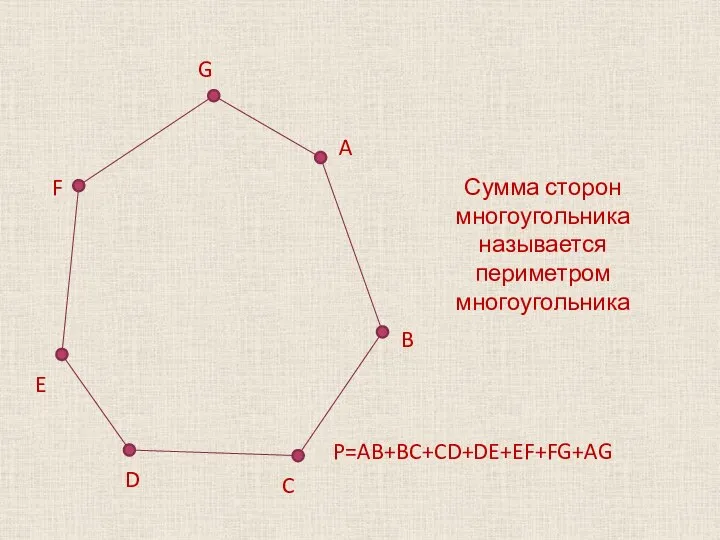
Сумма сторон многоугольника называется периметром многоугольника
P=AB+BC+CD+DE+EF+FG+AG
C
D

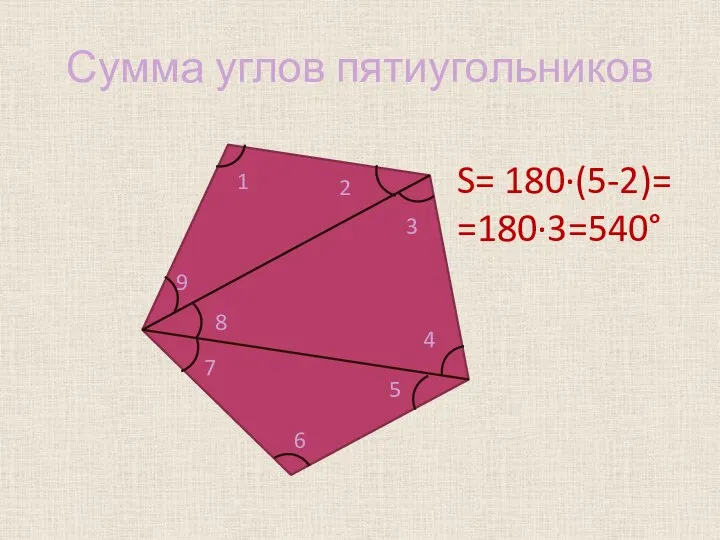
Сумма углов пятиугольников
1
2
3
4
5
6
7
8
9
S= 180·(5-2)=
=180·3=540°

Сумма углов шестиугольника
S= 180·(6-2)=
=180·4=720°

Сумма углов четырехугольников
S= 180·(4-2)=
=180·2=360°

S= 180·(5-2)=180·3=540°
S= 180·(6-2)=180·4=720°
S= 180·(4-2)=180·2=360°

S=180°·(n-2)
Сумма углов выпуклого n-угольника:

№365(в).
Дано:
n-угольник,
α=120°,
Найти n.
Решение:
120n=(n-2)180
120n=180n-360
360=180n-120n
360=60n
n=6
Ответ: 6 сторон

Критерии оценок, самостоятельной работы
За 4 правильных задания - оценка «5»
За 3 правильных задания – оценка «4»
За 2 правильных задания – оценка «3»
Если решено меньше двух заданий, то материал урока усвоен плохо, нужно дома очень постараться

Домашнее задание
Стр 100 № 364, 368