Содержание
- 2. Мода - значение признака (варианта), чаще всего встречающееся в изучаемой совокупности. Структурные средние: мода
- 3. Например: Распределение проданной женской обуви по размерам характеризуется следующим образом: Структурные средние: мода
- 4. Определение моды в интервальном ряду: ХMo - нижняя граница модального интервала; hMo - величина модального интервала;
- 5. Распределение рабочих по стажу работы характеризуется следующими данными. Структурные средние: мода
- 6. Медиана – это варианта, расположенная в середине упорядоченного ряда данных, которая делит статистическую совокупность на две
- 7. Номер медианной единицы определяют по формуле: Структурные средние: медиана
- 8. Например: Стаж пяти рабочих составил 4, 2, 10, 9,7 лет. Для определения медианы произведём ранжирование данных
- 9. Например: Стаж работы шести рабочих составил 1, 3, 4, 5, 10, 11лет. Сначала определяется номер медианной
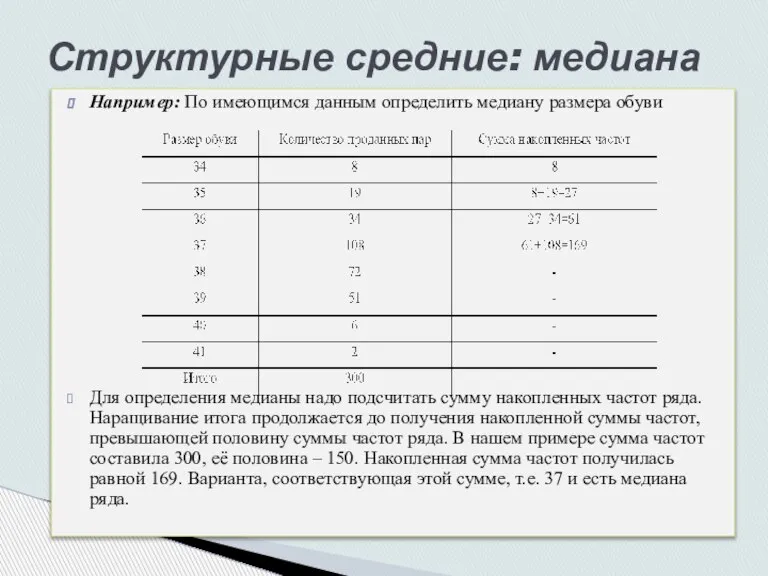
- 10. Например: По имеющимся данным определить медиану размера обуви Для определения медианы надо подсчитать сумму накопленных частот
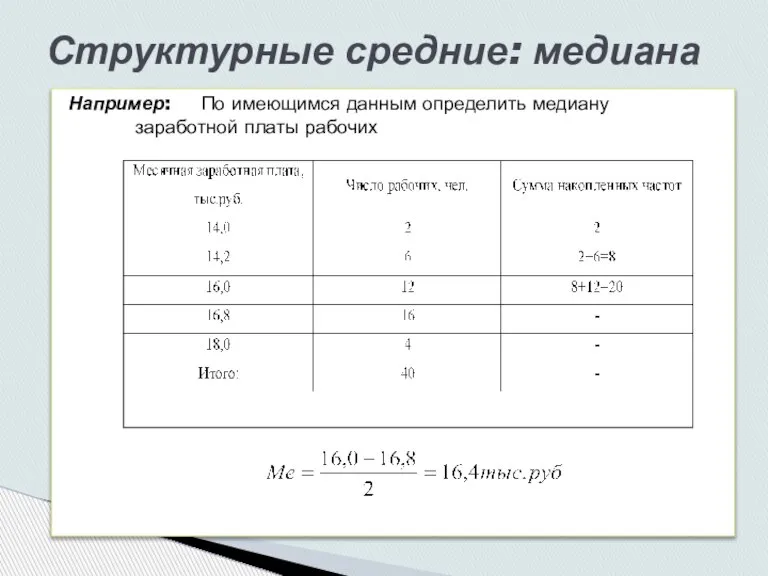
- 11. Например: По имеющимся данным определить медиану заработной платы рабочих Структурные средние: медиана
- 12. Расчет медианы интервального вариационного ряда распределения Где ХМе – нижняя граница медианного интервала; hMe – величина
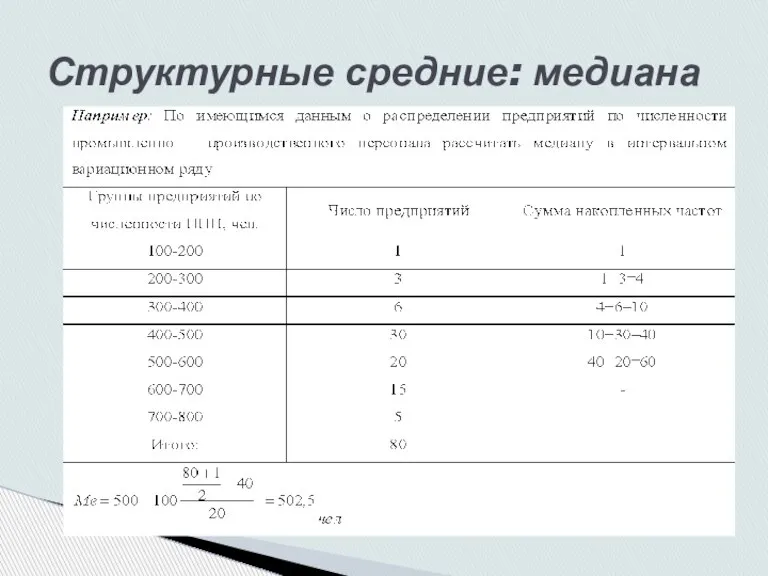
- 13. Например: По имеющимся данным о распределении предприятий по численности промышленно – производственного персонала рассчитать медиану в
- 14. Если сумма накопленных частот напротив одного из интервалов равна точно половине суммы частот ряда, то медиана
- 15. Структурные средние: медиана
- 16. квартили децили перцентили Квантиль – это значение признака, занимающее определенное место в упорядоченной по данному признаку
- 17. Расчет квартилей производиться по следующим формулам Первый квартиль: Третий квартиль: квартили – значения признака, делящие упорядоченную
- 19. Скачать презентацию













 Действительные числа. Практикум по математике. Занятие №1
Действительные числа. Практикум по математике. Занятие №1 Свойство медиан треугольника
Свойство медиан треугольника Тригонометрические уравнения, сводящиеся к квадратным
Тригонометрические уравнения, сводящиеся к квадратным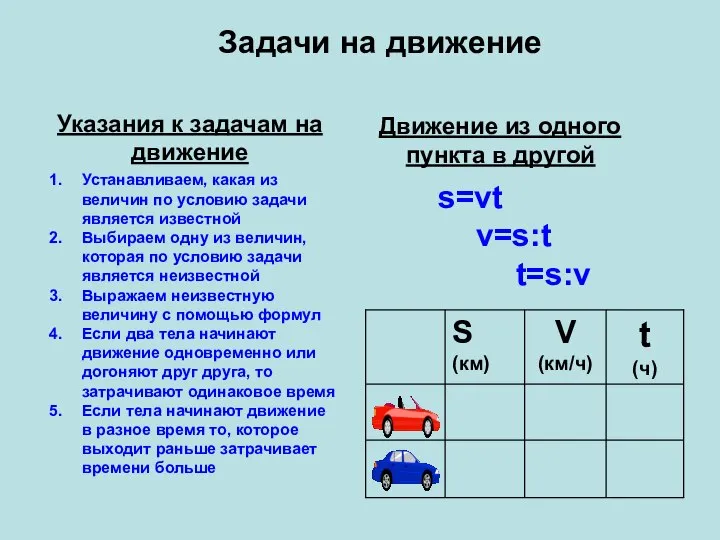 Задачи на движение Указания к задачам на движение
Задачи на движение Указания к задачам на движение Уменьшаемое, вычитаемое, разность
Уменьшаемое, вычитаемое, разность Тела вращения. Урок 142
Тела вращения. Урок 142 Уравнение линии на плоскости
Уравнение линии на плоскости За сокровищами (2 часть). Дроби
За сокровищами (2 часть). Дроби Скалярное произведение векторов. Решение задач
Скалярное произведение векторов. Решение задач Геометрические тела
Геометрические тела Аксиомы стереометрии. Некоторые следствия из аксиом
Аксиомы стереометрии. Некоторые следствия из аксиом Случаи вычитания 15-
Случаи вычитания 15- Трапеция. Свойства
Трапеция. Свойства Трапеция, ее элементы и виды, свойства и признаки
Трапеция, ее элементы и виды, свойства и признаки Цилиндр
Цилиндр Векторы в пространстве. Решение задач по готовым чертежам
Векторы в пространстве. Решение задач по готовым чертежам Действия с десятичными дробями. Математические гонки
Действия с десятичными дробями. Математические гонки Математика для родителей
Математика для родителей Повторение изученного в 5 классе
Повторение изученного в 5 классе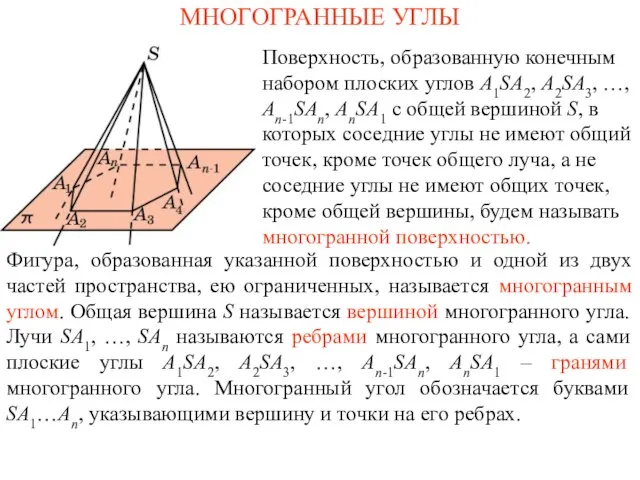 Презентация на тему Многогранные углы
Презентация на тему Многогранные углы  Размещения
Размещения Расчет центральной предельной теоремы
Расчет центральной предельной теоремы Квадратные уравнения. Повторение. 8 класс
Квадратные уравнения. Повторение. 8 класс Úsh perpendıkýlıar týraly teorema
Úsh perpendıkýlıar týraly teorema Обратные тригонометрические функции
Обратные тригонометрические функции Вычисление интегралов вида R(x, Jax2 + bx+c) dx
Вычисление интегралов вида R(x, Jax2 + bx+c) dx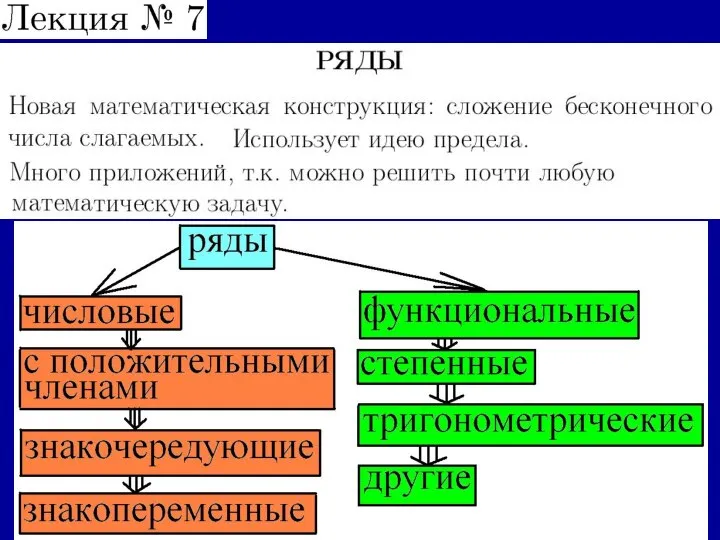 Числовые ряды
Числовые ряды Простейшие задачи в координатах
Простейшие задачи в координатах