Содержание
- 2. Девизом нашего урока будут такие слова: Думать - коллективно! Решать - оперативно! Отвечать - доказательно! Бороться
- 3. Прямой пропорциональностью называют функцию вида y= kx Графиком функции прямой пропорциональности является прямая Для построения графика
- 4. Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции. Задача1 Турист проехал на автобусе 15
- 5. Задача 2. Мама купила несколько конфет по цене 5 рублей за конфету и одну шоколадку по
- 6. Итак, мы получили две формулы, выражающие совершенно различные факты и явления, но имеющие одинаковую структуру: s=4t+65
- 7. Функция вида y = kx +b, где k и b числа, а x и y переменные,
- 8. у = 2 х + 3 х = у = 2 · +3 х 0 =
- 9. Совет: Если коэффициент k положительный, выбирай положительное значение аргумента; если отрицательный - отрицательное
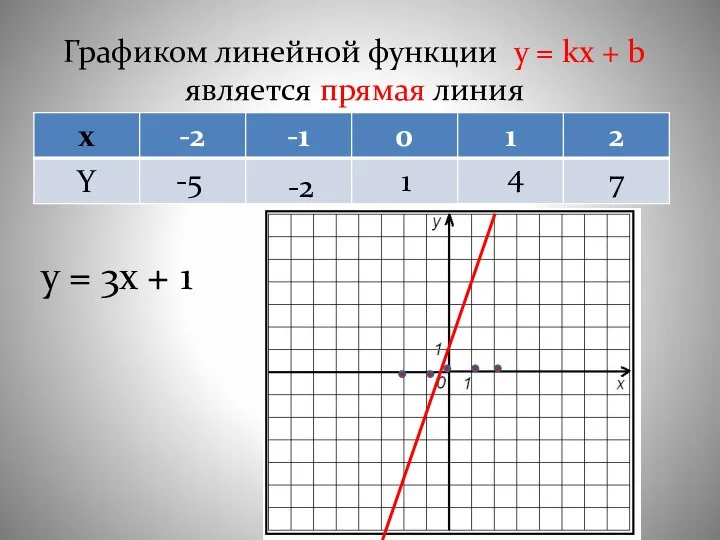
- 10. Графиком линейной функции y = kx + b является прямая линия y = 3x + 1
- 11. Через две точки можно провести только одну прямую линию Для построения графика линейной функции достаточно двух
- 12. Коэффициент k называют угловым коэффициентом.
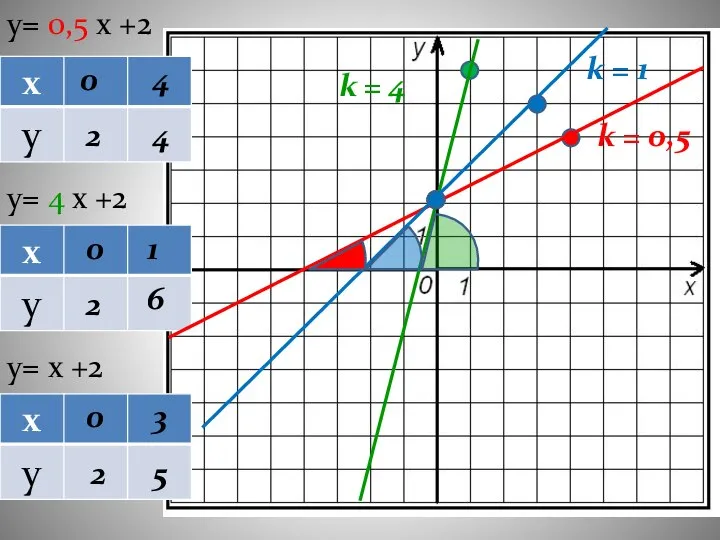
- 13. y= 0,5 х +2 y= 4 х +2 y= х +2 0 2 4 4 0
- 14. Чем больше угловой коэффициент k, тем больше угол, образованный графиком функции с осью ОХ
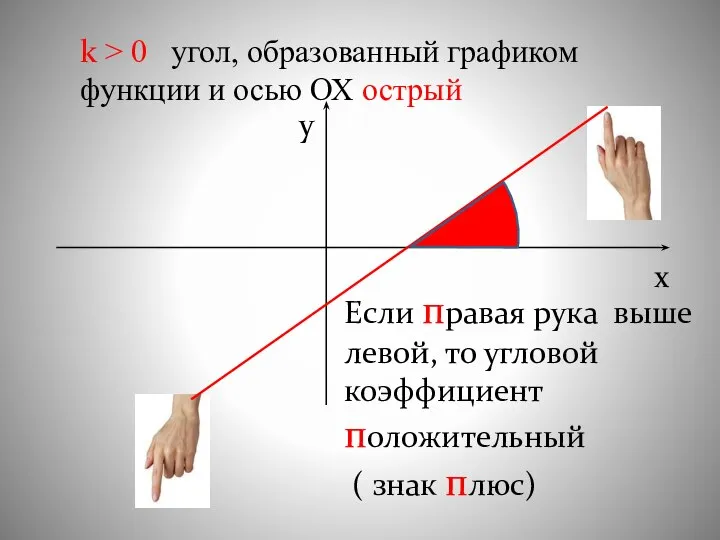
- 15. k > 0 угол, образованный графиком функции и осью ОХ острый х y Если правая рука
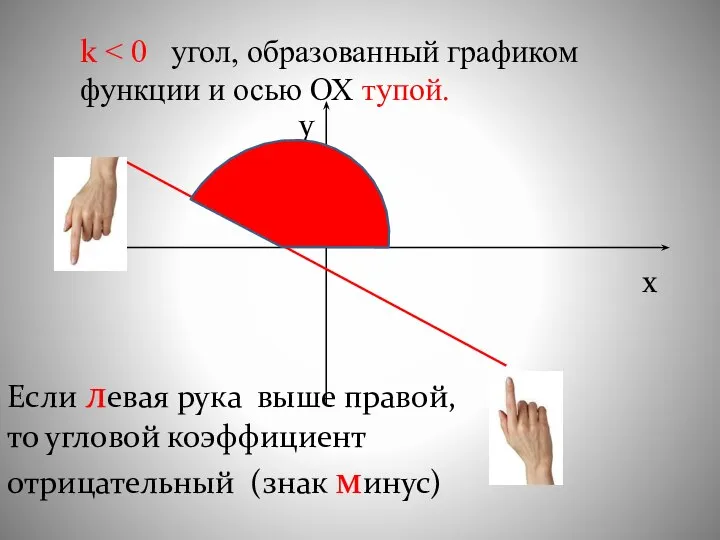
- 16. k x y Если левая рука выше правой, то угловой коэффициент отрицательный (знак минус)
- 17. k = 0 - график параллелен оси ОХ x y k = 0
- 18. Построим несколько графиков линейных функций, у которых одинаковые угловые коэффициенты.
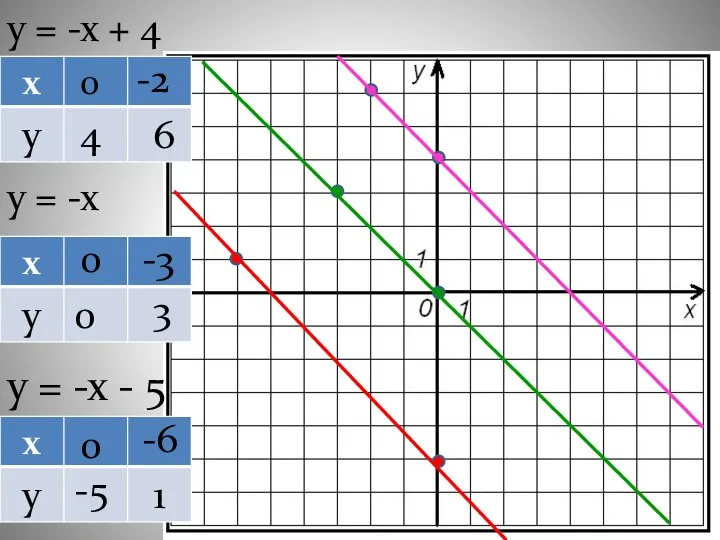
- 19. у = -х + 4 у = -х у = -х - 5 0 4 -2
- 20. Если у линейных функций угловой коэффициент одинаковый, то их графики параллельны!
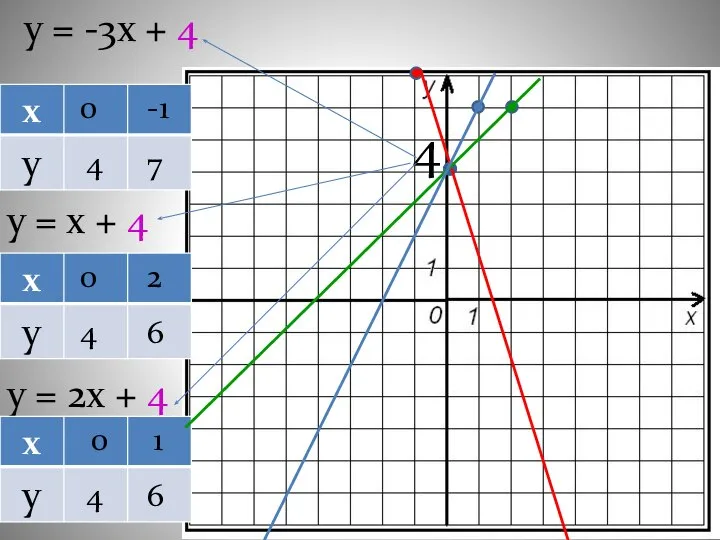
- 21. у = -3х + 4 у = х + 4 у = 2х + 4 0
- 22. График линейной функции пересекает ось OY в точке (0;b). х =0 , y = k ·
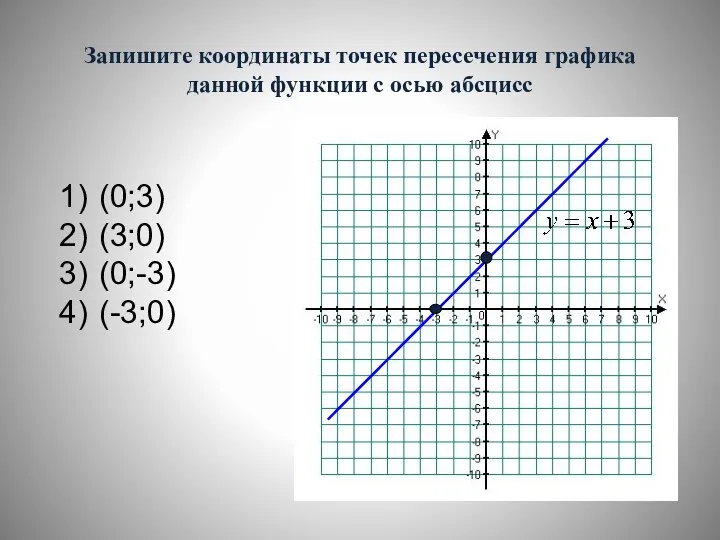
- 26. Запишите координаты точек пересечения графика данной функции с осью абсцисс (0;3) (3;0) (0;-3) (-3;0)
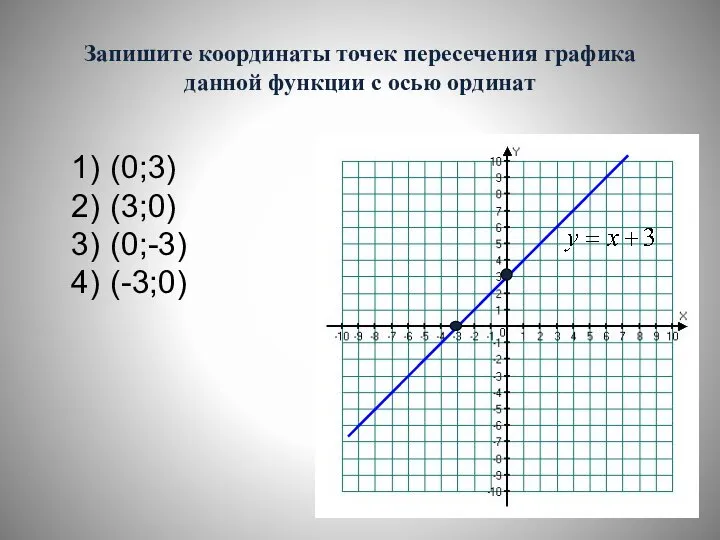
- 27. Запишите координаты точек пересечения графика данной функции с осью ординат (0;3) (3;0) (0;-3) (-3;0)
- 30. Скачать презентацию






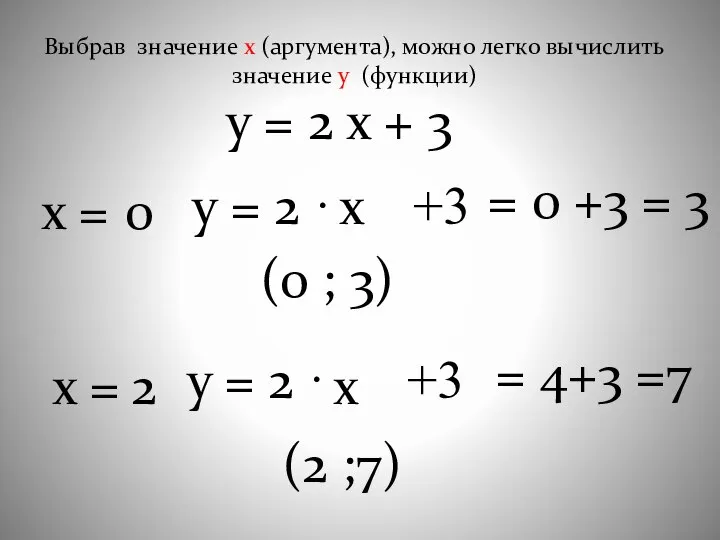




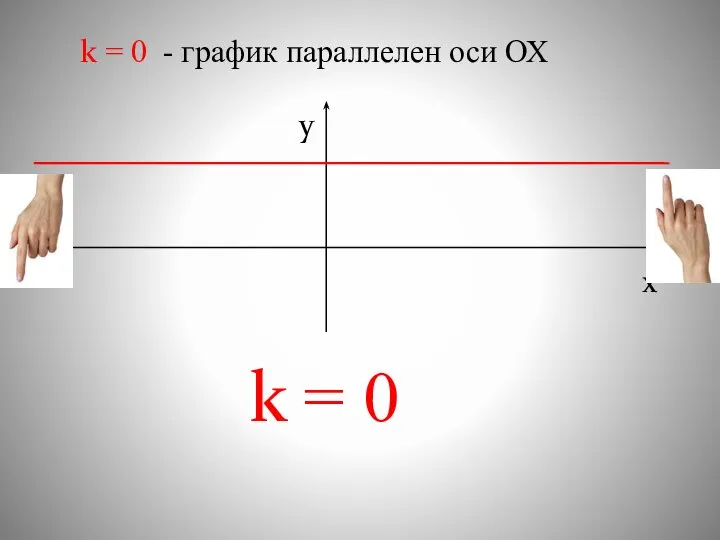







 Презентация на тему Решение задач части В
Презентация на тему Решение задач части В  Графики и диаграммы. Задания
Графики и диаграммы. Задания Вероятность случайного события
Вероятность случайного события Повторение. Числа от 100 до 1000 (Урок 1)
Повторение. Числа от 100 до 1000 (Урок 1) Геометрические построения
Геометрические построения Элементы комбинаторики. Правила
Элементы комбинаторики. Правила Тригонометрия в различных областях науки и жизни
Тригонометрия в различных областях науки и жизни Теорема Пифагора
Теорема Пифагора Решение задач на применение признаков равенства треугольников
Решение задач на применение признаков равенства треугольников Свойства числовых неравенств
Свойства числовых неравенств Фундаментальные и прикладные исследования в метрологии
Фундаментальные и прикладные исследования в метрологии Знакомство с предметом математика
Знакомство с предметом математика Основное свойство дроби
Основное свойство дроби Умножение обыкновенных дробей
Умножение обыкновенных дробей Эконометрика. Семинар 2. Решение задачи 4
Эконометрика. Семинар 2. Решение задачи 4 Теорема Пифагора
Теорема Пифагора Графический способ решения линейных уравнений с модулями
Графический способ решения линейных уравнений с модулями Логарифм числа. Свойства логарифмов
Логарифм числа. Свойства логарифмов Точка, отрезок, луч, прямая
Точка, отрезок, луч, прямая Дивергентные математические задачи как средство развития креативности мышления у младших школьников
Дивергентные математические задачи как средство развития креативности мышления у младших школьников Прямые на плоскости
Прямые на плоскости Геометрические фигуры
Геометрические фигуры Задачи на нахождение расстояния между вершинами многогранника, все двугранные углы которого, прямые
Задачи на нахождение расстояния между вершинами многогранника, все двугранные углы которого, прямые Парный регрессионный анализ
Парный регрессионный анализ Презентация на тему Дроби
Презентация на тему Дроби  Цилиндр. Урок – практикум. Итоговое повторение. 11 класс
Цилиндр. Урок – практикум. Итоговое повторение. 11 класс Матрицы и действия с матрицами
Матрицы и действия с матрицами Пифагор и литература
Пифагор и литература