Построение графика квадратичной функции

АЛГОРИТМ ПОСТРОЕНИЯ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
y = ax2+bx+c, определить вид графика и направление ветвей.
Определить координаты вершины параболы : х0 = -b/2a; у0 = y(х0) , отметить ее в координатной плоскости, провести ось симметрии.
Найти точки пересечения с осями ОХ и ОУ.
Соединить отмеченные точки.

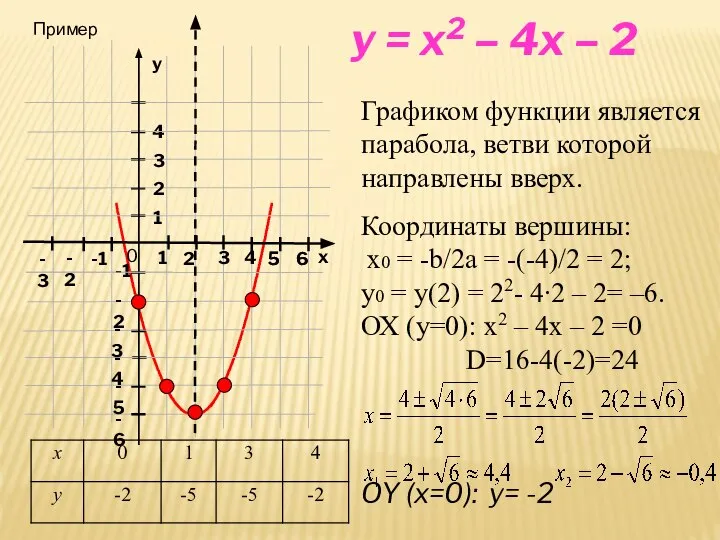
x
y = x2 – 4x – 2
Графиком функции является парабола, ветви которой направлены вверх.
Координаты вершины:
х0 = -b/2a = -(-4)/2 = 2;
у0 = y(2) = 22- 4∙2 – 2= –6.
ОХ (у=0): x2 – 4x – 2 =0
D=16-4(-2)=24
OY (x=0): y= -2
Пример

СВОЙСТВА КВАДРАТИЧНОЙ ФУНКЦИИ
Область определения D(y) = (- ∞;+ ∞).
Область значений Е(у): [-6; +∞)
у>0 при х∈(- ∞;-0,4)∪ (4,4;+ ∞)
у<0 при х∈(0,4; 4,4)
3. у при х ∈(2; + ∞)
4. у при х ∈(-∞; 2)
5. унаим= -6, если х= 2
6. унаиб – не существует.

ПОСТРОИТЬ ГРАФИКИ ФУНКЦИЙ И ОПИСАТЬ СВОЙСТВА