Содержание
- 2. Возведите во вторую степень данные выражения: (3х+7) (2х-5)
- 3. Иррациональное уравнения- это уравнения, в которых неизвестное находится под знаком корня.
- 4. Свойство: При возведении обеих частей уравнения в натуральную степень получается уравнение-следствие данного.
- 5. Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называют
- 6. Пример. 1)Решить уравнение: Решение: Х+2=52, т.е. х=25-2. Ответ : х=23
- 7. II. Решение уравнений вида Решать это уравнение будем возведением обеих частей во вторую степень, как уже
- 8. Ответ: нет решений. Приравниваем выражения, стоящие под корнем: Х-5=2х-3, Х=-2 Проверка: При х=-2 оба выражения, стоящие
- 9. Решите уравнение Сделайте проверку: Ответ: х=3
- 10. Решите уравнение Решение: 2х+3=1, 2х=-2, х=-1. Ответ: х=-1. Проверка: 1=1, х=-1 – корень уравнения.
- 11. Иногда иррациональные уравнения можно решать так называемым графическим методом. На стр. 62, задача№4. ВАЖНО! Этот способ
- 12. Решаем №152(1), №153(2), №155(1)
- 14. Скачать презентацию











 Найдите объем тела вращения вокруг оси 0х , ограниченной прямыми
Найдите объем тела вращения вокруг оси 0х , ограниченной прямыми Консультация ДУ
Консультация ДУ Необыкновенное путешествие Зимы. Цифры для дошкольников
Необыкновенное путешествие Зимы. Цифры для дошкольников Площади треугольников
Площади треугольников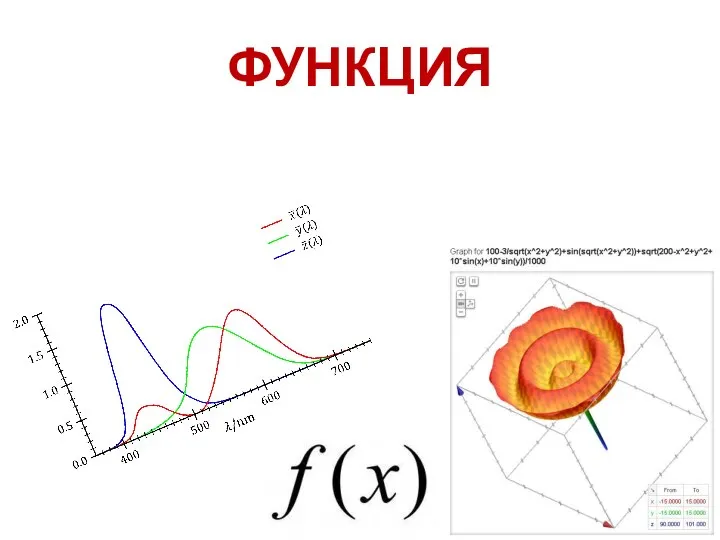 Понятие функции
Понятие функции Степень с рациональным показателем
Степень с рациональным показателем Геометрический смысл производной
Геометрический смысл производной Производная суммы, произведения и частного двух функций
Производная суммы, произведения и частного двух функций Задачи на количество предметов
Задачи на количество предметов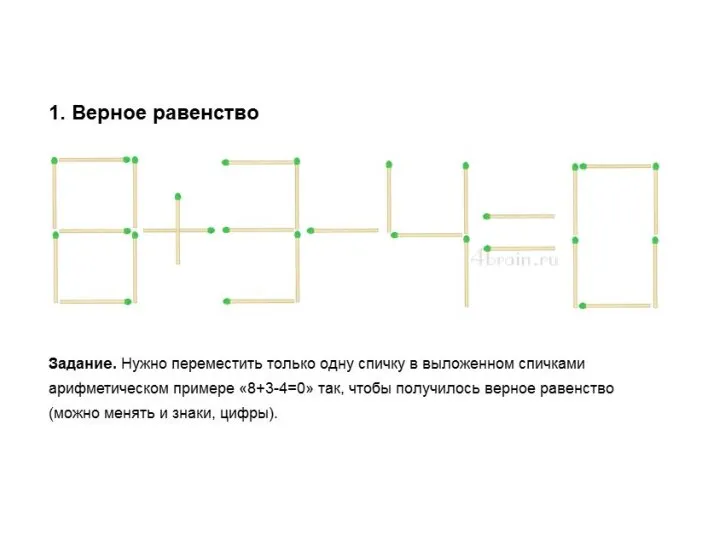 Спички
Спички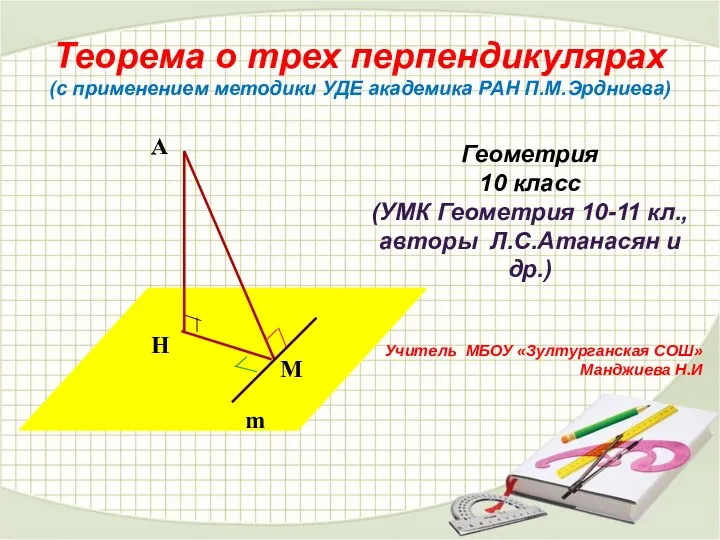 Теорема о трех перпендикулярах (с применением методики УДЕ академика РАН П.М. Эрдниева)
Теорема о трех перпендикулярах (с применением методики УДЕ академика РАН П.М. Эрдниева)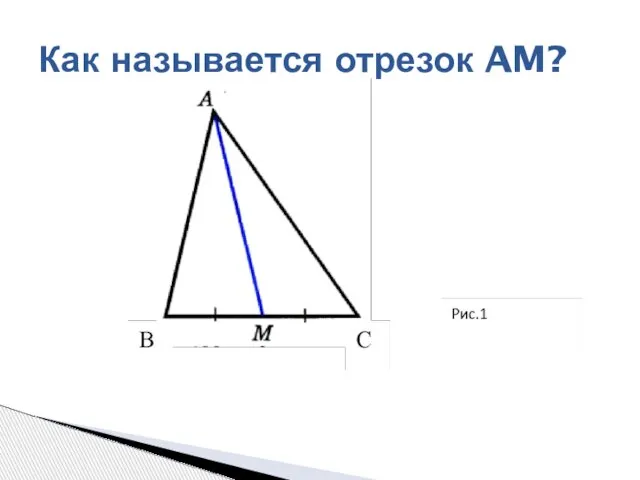 Равнобедренный треугольник и его свойства
Равнобедренный треугольник и его свойства Что умеет линейка?
Что умеет линейка? Перестановка и группировка множителей
Перестановка и группировка множителей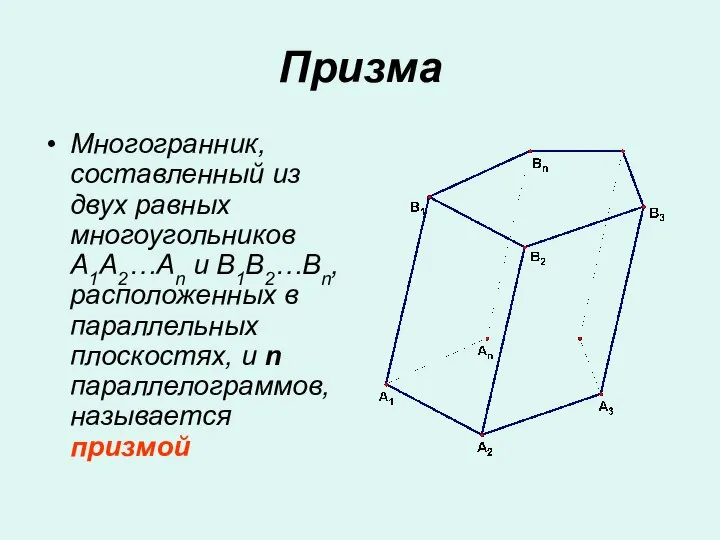 Призма. Боковые ребра призмы
Призма. Боковые ребра призмы Функция у = √х, ее свойства и график
Функция у = √х, ее свойства и график Куб. Измерения куба
Куб. Измерения куба Игра-тренажер А знаете ли вы…. Математика 3 класс
Игра-тренажер А знаете ли вы…. Математика 3 класс Решение задач на построение методом подобных треугольников
Решение задач на построение методом подобных треугольников Математическая психология
Математическая психология По следам телепередач. Поле чудес
По следам телепередач. Поле чудес Цирк. Геометрические фигуры
Цирк. Геометрические фигуры Калькуляционная карточка. Тесто заварное
Калькуляционная карточка. Тесто заварное Разложение многочлена на множители с помощью формулы сокращенного умножения
Разложение многочлена на множители с помощью формулы сокращенного умножения 20120818_pryamaya_i_obratnaya_proporcionalnost
20120818_pryamaya_i_obratnaya_proporcionalnost Дифференциальные уравнения
Дифференциальные уравнения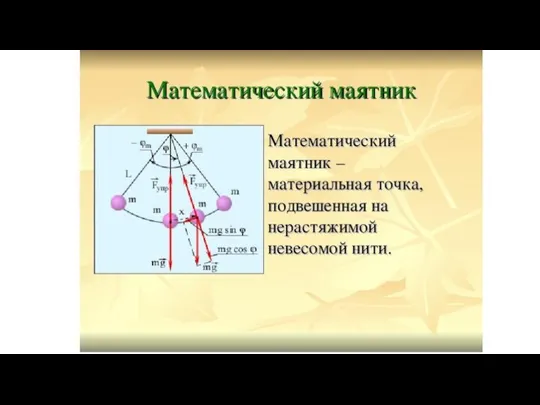 Математический маятник
Математический маятник Презентация на тему Прямоугольный треугольник - готовая презентация, для решения на готовых чертежах.
Презентация на тему Прямоугольный треугольник - готовая презентация, для решения на готовых чертежах.