Наибольшее и наименьшее значения функции

Цели обучения:
10.3.1.19 - находить наибольшее и наименьшее значения функции на отрезке;
10.3.3.3 - решать прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции

Критерии оценивания:
Учащийся достиг цели обучения, если:
- умеет находить наибольшее и наименьшее значение функции на заданном промежутке;
- решать разные задачи, связанные с наибольшим (наименьшим) значением функции на промежутке.

Вейерштрасс Карл Теодор Вильгельм (1815-1897 гг.) - немецкий математик
Теорема Вейерштрасса
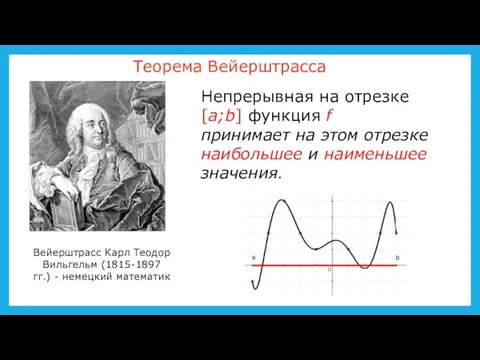
Непрерывная на отрезке [a;b] функция f принимает на этом отрезке наибольшее и наименьшее значения.

Если функция f(x) возрастает (убывает) на [a;b], то наибольшего или наименьшего значения она достигает на концах этого отрезка.

Если функция у = f(х) на отрезке [а; b] имеет лишь одну критическую точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение
fmax = fнаиб. fmin = fнаим.

Наибольшего (наименьшего) значения непрерывная на [а; b] функция достигает либо на концах отрезка, либо в критических точках, лежащих на этом отрезке.

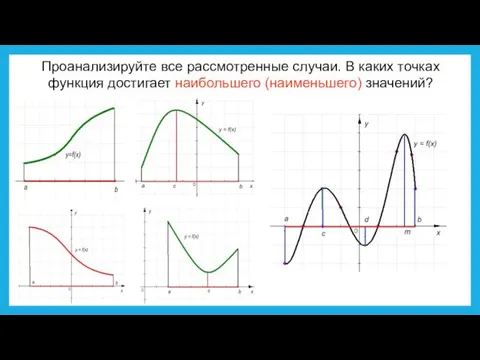
Проанализируйте все рассмотренные случаи. В каких точках функция достигает наибольшего (наименьшего) значений?

Алгоритм нахождения наибольшего и наименьшего значения функции на [a;b]

Задача 1.

Задача 2.
Решение задач практического характера
Задача 3.