Слайд 2Пусть у нас есть график некоторой функции f(x) на промежутке [a; b].
![Пусть у нас есть график некоторой функции f(x) на промежутке [a; b].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1009274/slide-1.jpg)
По графику легко найти наибольшее и наименьшее значения функции на промежутке. Иногда наибольшее и наименьшее значения можно отыскать и без построения графика.
Слайд 3Для того, чтобы избежать построения графика функции воспользуемся следующими утверждениями.
Если функция непрерывна

на отрезке, то она достигает на нем и своего наибольшего, и своего наименьшего значений.
2. Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
3. Если наибольшее или наименьшее значение достигается внутри отрезка, то только в стационарной или критической точке.
Слайд 4Это утверждение можно проиллюстрировать графиками функций.
Видно, что на первом графике наибольшее и
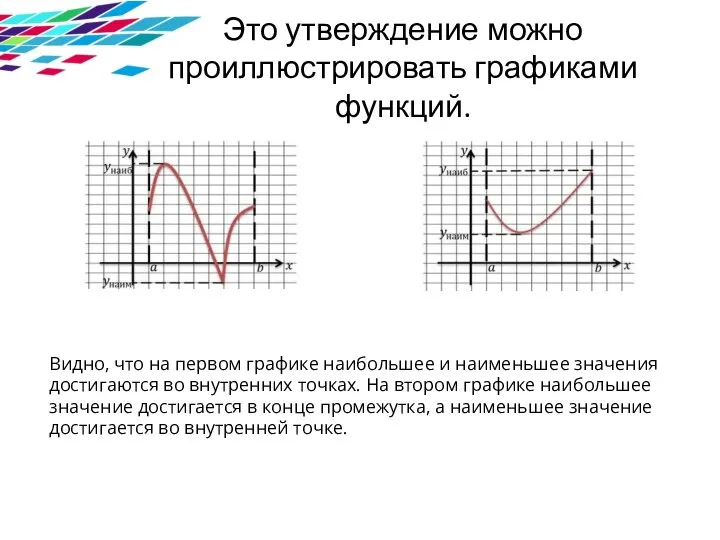
наименьшее значения достигаются во внутренних точках. На втором графике наибольшее значение достигается в конце промежутка, а наименьшее значение достигается во внутренней точке.
Слайд 5Алгоритм нахождения наименьшего и наибольшего значений непрерывной функции
у = f(x) на
![Алгоритм нахождения наименьшего и наибольшего значений непрерывной функции у = f(x) на отрезке [a; b].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1009274/slide-4.jpg)
отрезке [a; b].
Слайд 7Надо найти наибольшее и наименьшее значения на незамкнутом интервале
Теорема.
Пусть функция y =

f(x) непрерывна на промежутке X и имеет внутри него единственную стационарную или критическую точку x = x0. Тогда:
а) если x = x0 − точка максимума, то yнаиб = f(x0);
б) если x = x0 − точка минимума, то yнаим = f(x0).
![Пусть у нас есть график некоторой функции f(x) на промежутке [a; b].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1009274/slide-1.jpg)


![Алгоритм нахождения наименьшего и наибольшего значений непрерывной функции у = f(x) на отрезке [a; b].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1009274/slide-4.jpg)
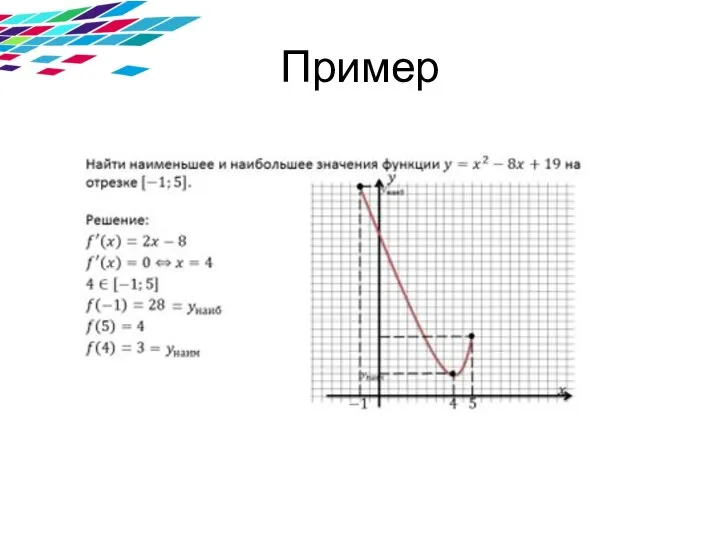

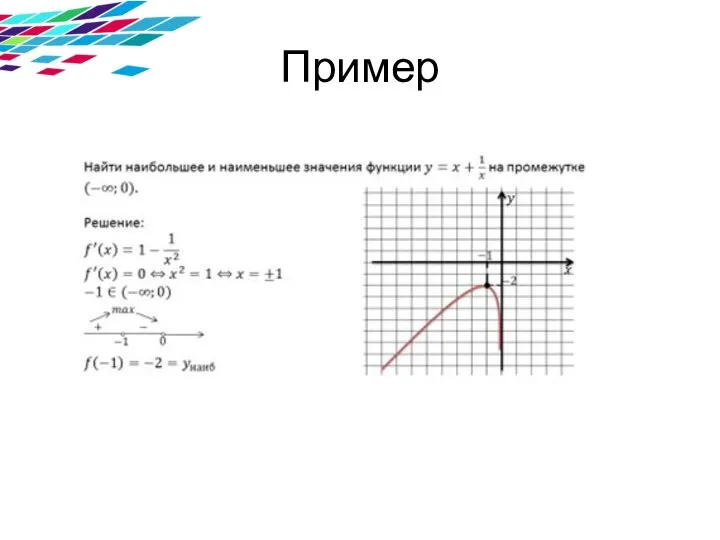

 Корень уравнения
Корень уравнения Презентация на тему Технологии развивающего обучения в практике учителя математики
Презентация на тему Технологии развивающего обучения в практике учителя математики  Двойные интегралы в прямоугольной области
Двойные интегралы в прямоугольной области Осевая симметрия
Осевая симметрия Робота учасника XVIII обласної математичної олімпіади Гарасюка Дмитра Андрійовича
Робота учасника XVIII обласної математичної олімпіади Гарасюка Дмитра Андрійовича Основные положения теории групп
Основные положения теории групп 20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами
20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами Правила сложения сил и условия равновесия твердых тел
Правила сложения сил и условия равновесия твердых тел Задачи. Геометрия 8 кл
Задачи. Геометрия 8 кл Подобие треугольников
Подобие треугольников Число пи вокруг нас
Число пи вокруг нас Своя игра по математике
Своя игра по математике Результаты пробных ЕГЭ по математике (2013-2014 учебный год)
Результаты пробных ЕГЭ по математике (2013-2014 учебный год) Презентация на тему Тест по теме "Площади"
Презентация на тему Тест по теме "Площади"  Презентация на тему Решение задач В ЕГЭ по теории вероятности
Презентация на тему Решение задач В ЕГЭ по теории вероятности  математика
математика Презентация на тему Уравнение множественной регрессии
Презентация на тему Уравнение множественной регрессии  Презентация на тему Обыкновенные дроби (6 класс)
Презентация на тему Обыкновенные дроби (6 класс)  Презентация на тему Все действия с десятичными дробями (5 класс)
Презентация на тему Все действия с десятичными дробями (5 класс)  Умножение одночлена на многочлен. Самостоятельная работа
Умножение одночлена на многочлен. Самостоятельная работа Вписанные окружности (решение задач)
Вписанные окружности (решение задач) Элементы аналитической геометрии. Уравнение прямой на плоскости
Элементы аналитической геометрии. Уравнение прямой на плоскости Урок - игра В мире математики 6 класс
Урок - игра В мире математики 6 класс Производная и исследование функции
Производная и исследование функции Принцип относительности Галилея
Принцип относительности Галилея Решение задач и примеров
Решение задач и примеров Взаимно-обратные задачи. 2 класс
Взаимно-обратные задачи. 2 класс