Слайд 2№ 1. Функция у = sin x
1 ед = 2 клетки π
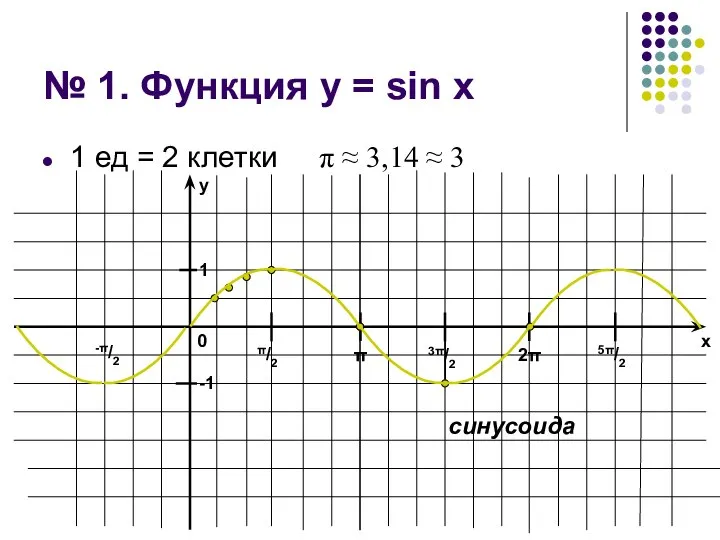
≈ 3,14 ≈ 3
х
у
π
2π
1
-1
π/2
3π/2
5π/2
0
синусоида
-π/2
Слайд 3№ 1. Функция у = sin х.
1. Область определения
D(f) = (–∞; +∞)

= R
2. Область значений
Е(f) = [–1; 1]
3. Точки пересечения с осями координат
Ох: x = πn, nЄZ
Оу: y = 0
Слайд 4№ 1. Функция у = sin х.
4. Промежутки знакопостоянства функции
f(х)>0 при хЄ(2πn;

π + 2πn), nЄZ
f(х)<0 при хЄ(π + 2πn; 2π + 2πn), nЄZ
5. Точки экстремума функции
x = π/2 + 2πn, nЄZ – точки max
x = 3π/2 + 2πn, nЄZ – точки min
6. Промежутки монотонности функции
f(х)↑ при хЄ(–π/2 + 2πn; π/2 + 2πn), nЄZ
f(х)↓ при хЄ(π/2 + 2πn; 3π/2 + 2πn), nЄZ
Слайд 5№ 1. Функция у = sin х.
7. Периодичность функции
Т = 2π
8. Четность

(нечетность) функции
Нечетная, т.к. график симметричен относительно начала координат
Слайд 6№ 2. Функция у = cos x
1 ед = 2 клетки π
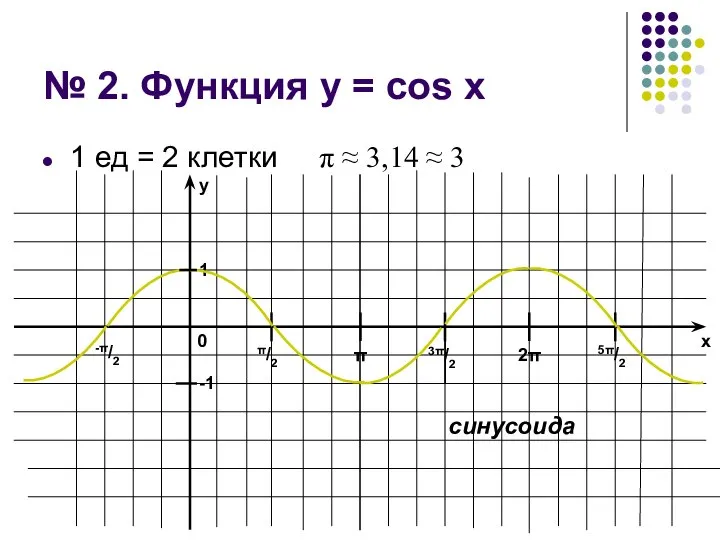
≈ 3,14 ≈ 3
х
у
π
2π
1
-1
π/2
3π/2
5π/2
0
синусоида
-π/2
Слайд 7№ 2. Функция у = cos х.
1. Область определения
D(f) = (–∞; +∞)

= R
2. Область значений
Е(f) = [–1; 1]
3. Точки пересечения с осями координат
Ох: x = π/2 + πn, nЄZ
Оу: y = 1
Слайд 8№ 2. Функция у = cos х.
4. Промежутки знакопостоянства функции
f(х)>0 при хЄ(–π/2

+ 2πn; π/2 + 2πn), nЄZ
f(х)<0 при хЄ(π/2 + 2πn; 3π/2 + 2πn), nЄZ
5. Точки экстремума функции
x = 0 + 2πn = 2πn, nЄZ – точки max
x = π + 2πn, nЄZ – точки min
6. Промежутки монотонности функции
f(х)↑ при хЄ(–π + 2πn; 2πn), nЄZ
f(х)↓ при хЄ(2πn; π + 2πn), nЄZ
Слайд 9№ 2. Функция у = cos х.
7. Периодичность функции
Т = 2π
8. Четность

(нечетность) функции
Функция четная, т.к. график симметричен относительно Оу.
Слайд 10№ 3. Функция у = tg x
1 ед = 2 клетки π
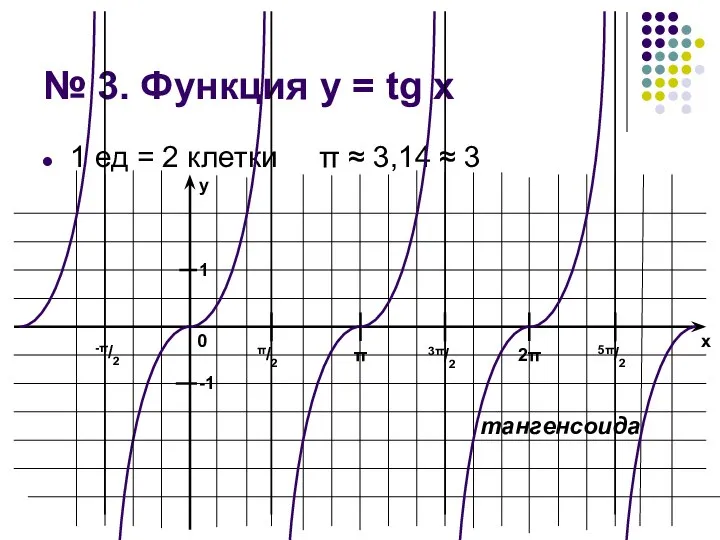
≈ 3,14 ≈ 3
х
у
π
2π
1
-1
π/2
5π/2
0
3π/2
тангенсоида
-π/2
Слайд 11№ 3. Функция у = tg х.
1. Область определения
D(f) = (–π/2 +

πn; π/2 + πn), nЄZ
2. Область значений
Е(f) = (–∞; +∞) = R
3. Точки пересечения с осями координат
Ох: x = 0 + πn = πn, nЄZ
Оу: y = 0
Слайд 12№ 3. Функция у = tg х.
4. Промежутки знакопостоянства функции
f(х)>0 при хЄ(πn;

π/2 + πn), nЄZ
f(х)<0 при хЄ(–π/2 + πn; πn), nЄZ
5. Точки экстремума функции
точек экстремума нет
6. Промежутки монотонности функции
возрастает при всех значениях области определения
Слайд 13№ 3. Функция у = tg х.
7. Периодичность функции
Т = π
8. Четность

(нечетность) функции
Нечетная, т.к. график симметричен относительно начала координат.
Слайд 14№ 4. Функция у = ctg x
1 ед = 2 клетки π
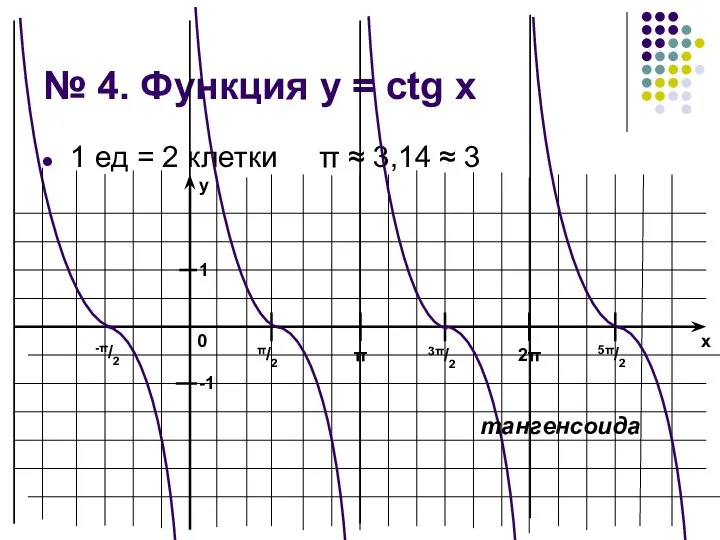
≈ 3,14 ≈ 3
х
у
π
2π
1
-1
π/2
5π/2
0
3π/2
тангенсоида
-π/2
Слайд 15№ 4. Функция у = ctg х.
1. Область определения
D(f) = (πn; π

+ πn), nЄZ
2. Область значений
Е(f) = (–∞; +∞) = R
3. Точки пересечения с осями координат
Ох: x = π/2 + πn, nЄZ
Оу: точек пересечения нет
Слайд 16№ 4. Функция у = ctg х.
4. Промежутки знакопостоянства функции
f(х)>0 при хЄ(πn;

π/2 + πn), nЄZ
f(х)<0 при хЄ(π/2 + πn; π + πn), nЄZ
5. Точки экстремума функции
точек экстремума нет
6. Промежутки монотонности функции
убывает при всех значениях области определения















 Понятие цилиндра
Понятие цилиндра Квадратичная функция у=х2 и ее свойства
Квадратичная функция у=х2 и ее свойства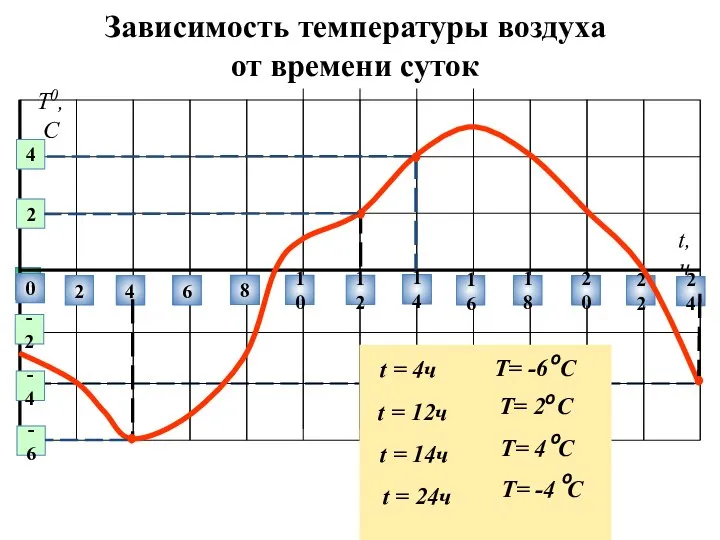 Зависимость температуры воздуха от времени суток
Зависимость температуры воздуха от времени суток Задачи на части
Задачи на части Осевая симметрия
Осевая симметрия Математическая игра Отгадайка
Математическая игра Отгадайка Найдите все значения параметра a,
Найдите все значения параметра a, А-11 Триг функции и их свойства 29.09.22 - копия
А-11 Триг функции и их свойства 29.09.22 - копия Евклидова геометрия
Евклидова геометрия Нахождение неизвестного вычитаемого
Нахождение неизвестного вычитаемого Способ вычисления двойных интегралов путем сведения их к повторному интегралу
Способ вычисления двойных интегралов путем сведения их к повторному интегралу Ромб, квадрат
Ромб, квадрат Четырёхугольники. Задачи на готовых чертежах
Четырёхугольники. Задачи на готовых чертежах Презентация на тему Учим состав числа от 5 до 10
Презентация на тему Учим состав числа от 5 до 10  Matplotlib
Matplotlib Применение теоремы синусов
Применение теоремы синусов Математическая логика и теория алгоритмов. Алгебра логики. Часть 2
Математическая логика и теория алгоритмов. Алгебра логики. Часть 2 Основные тригонометрические тождества. Преобразование тригонометрических выражений
Основные тригонометрические тождества. Преобразование тригонометрических выражений Презентация на тему Решение неравенств методом интервалов (9 класс)
Презентация на тему Решение неравенств методом интервалов (9 класс)  Решение прямоугольных треугольников
Решение прямоугольных треугольников Ряды
Ряды Презентация на тему Сдвиг графика функции y = x вдоль осей координат
Презентация на тему Сдвиг графика функции y = x вдоль осей координат  Гипотеза Пуанкаре
Гипотеза Пуанкаре Экзамен по математике
Экзамен по математике Подготовка к ГИА
Подготовка к ГИА Решение систем уравнений и неравенств графическим способом
Решение систем уравнений и неравенств графическим способом Презентация на тему Движение фигур в стереометрии
Презентация на тему Движение фигур в стереометрии  Презентация на тему Прямоугольный треуголиник: синус, косинус, тангенс угла
Презентация на тему Прямоугольный треуголиник: синус, косинус, тангенс угла