Содержание
- 2. Наслідок 1 а А а А Через пряму a і точку А, проведено ЄДИНУ можливу площину.
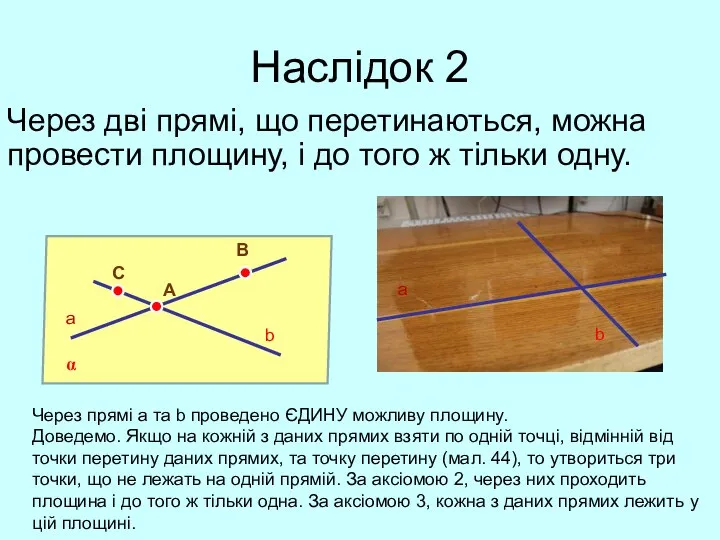
- 3. Наслідок 2 Через дві прямі, що перетинаються, можна провести площину, і до того ж тільки одну.
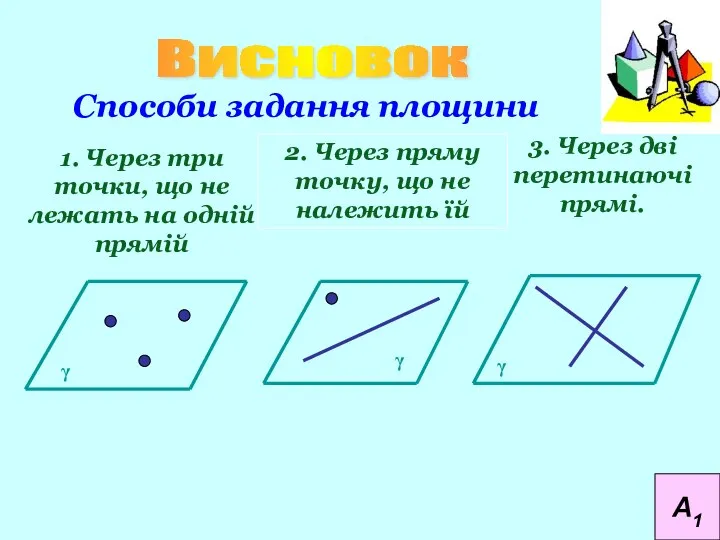
- 4. Способи задання площини 1. Через три точки, що не лежать на одній прямій 2. Через пряму
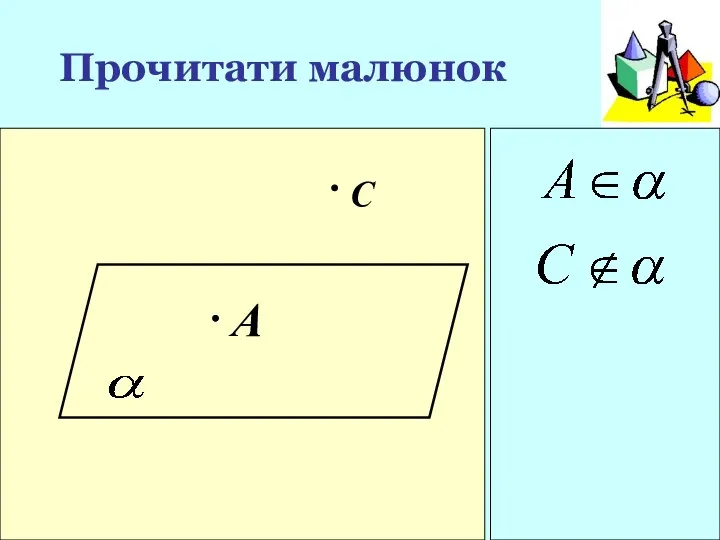
- 5. Прочитати малюнок A С
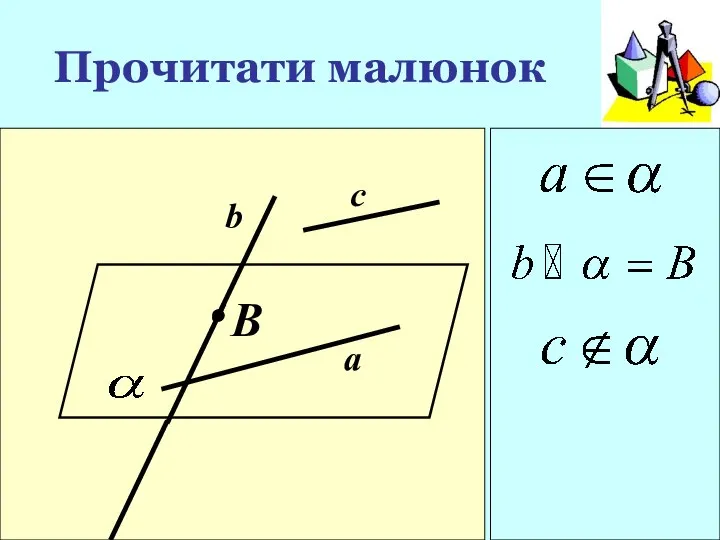
- 6. Прочитати малюнок B c b a
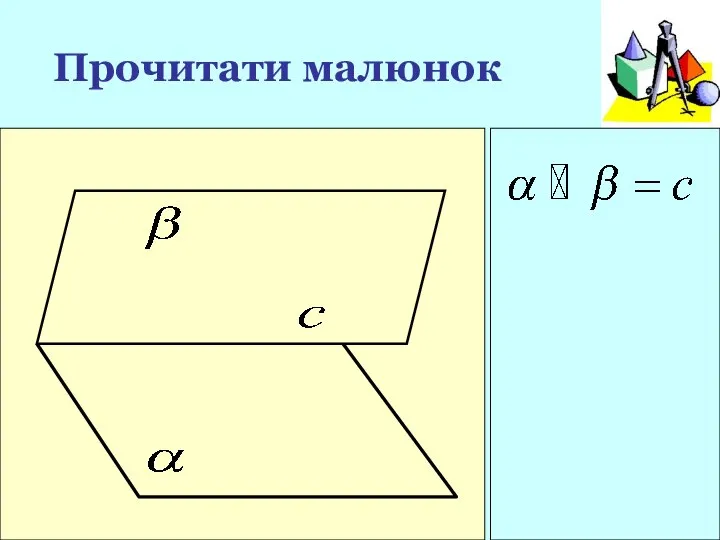
- 7. Прочитати малюнок
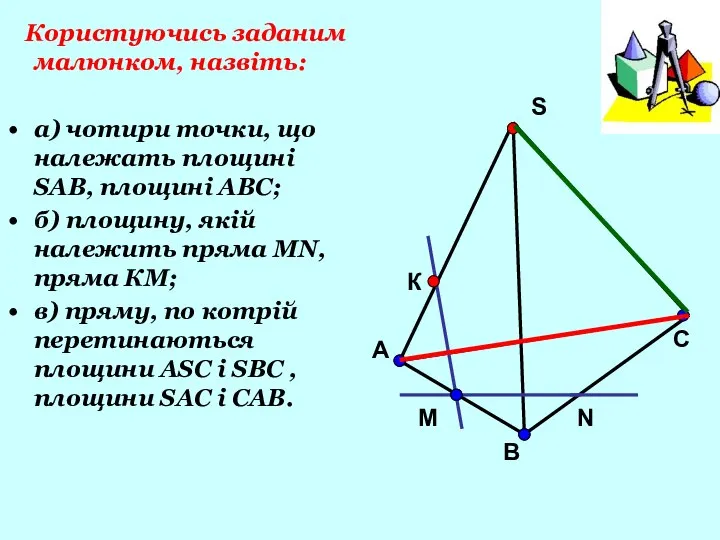
- 8. Користуючись заданим малюнком, назвіть: а) чотири точки, що належать площині SAB, площині АВС; б) площину, якій
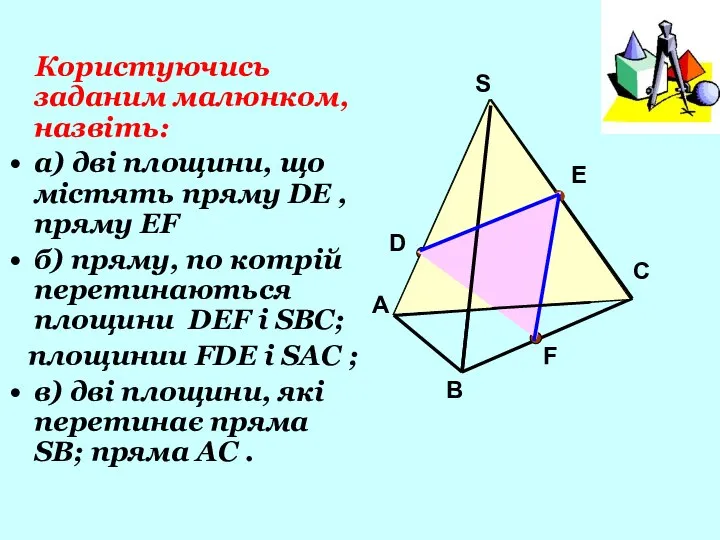
- 9. Користуючись заданим малюнком, назвіть: а) дві площини, що містять пряму DE , пряму EF б) пряму,
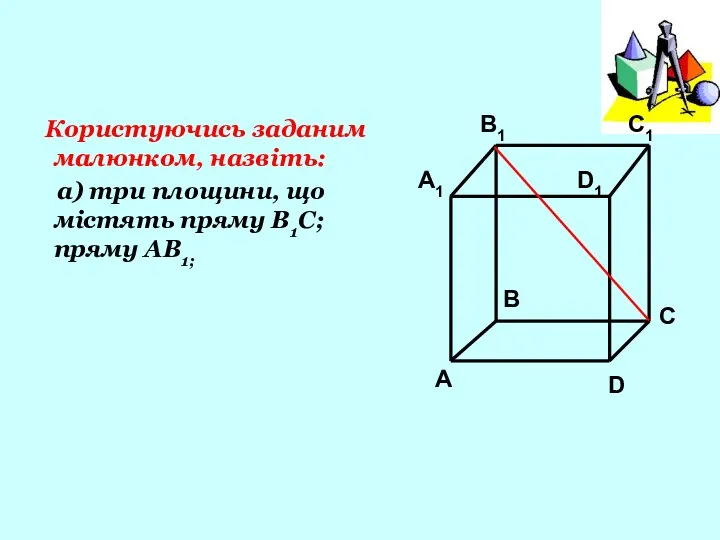
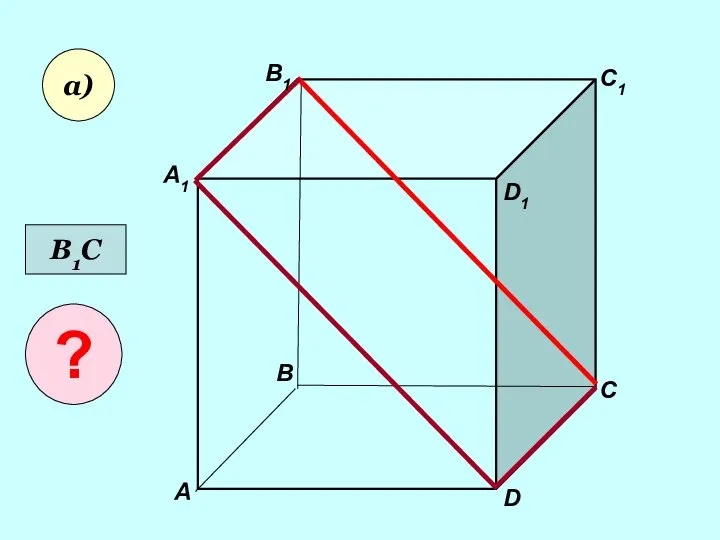
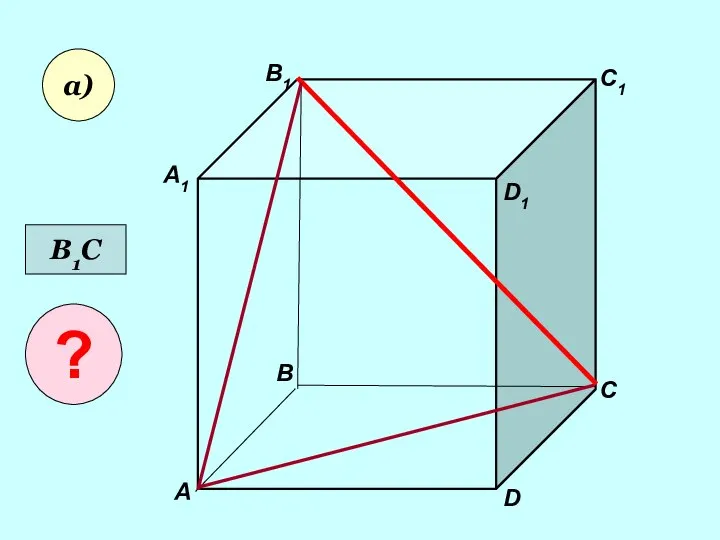
- 10. Користуючись заданим малюнком, назвіть: а) три площини, що містять пряму В1С; пряму АВ1;
- 11. А А1 В В1 С D1 D C1 а) В1С ?
- 12. А А1 В В1 С D1 D C1 а) В1С ?
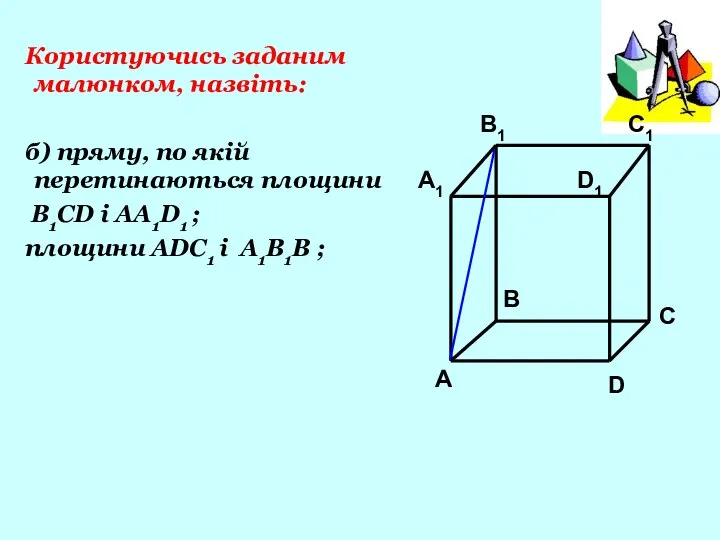
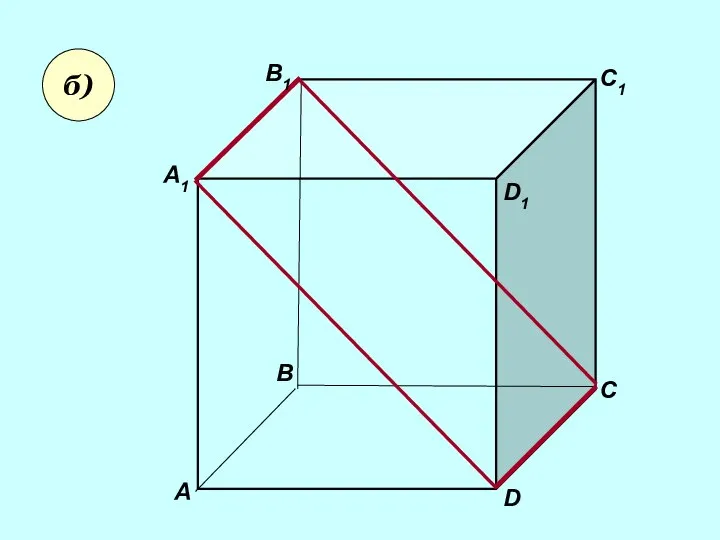
- 13. Користуючись заданим малюнком, назвіть: б) пряму, по якій перетинаються площини B1CD і AA1D1 ; площини ADC1
- 14. А А1 В В1 С D1 D C1 б)
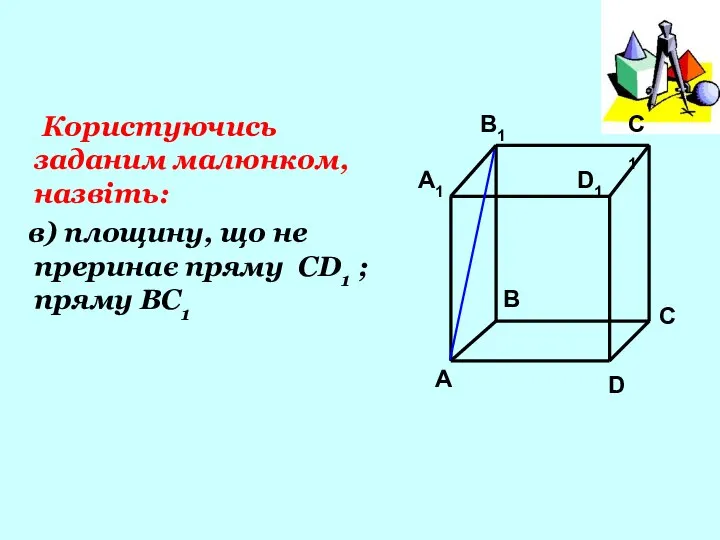
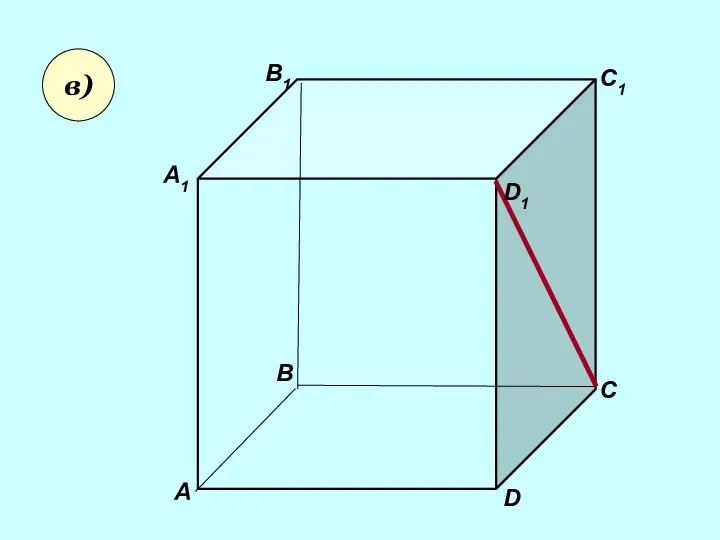
- 15. Користуючись заданим малюнком, назвіть: в) площину, що не преринає пряму CD1 ; пряму BC1
- 16. А А1 В В1 С D1 D C1 в)
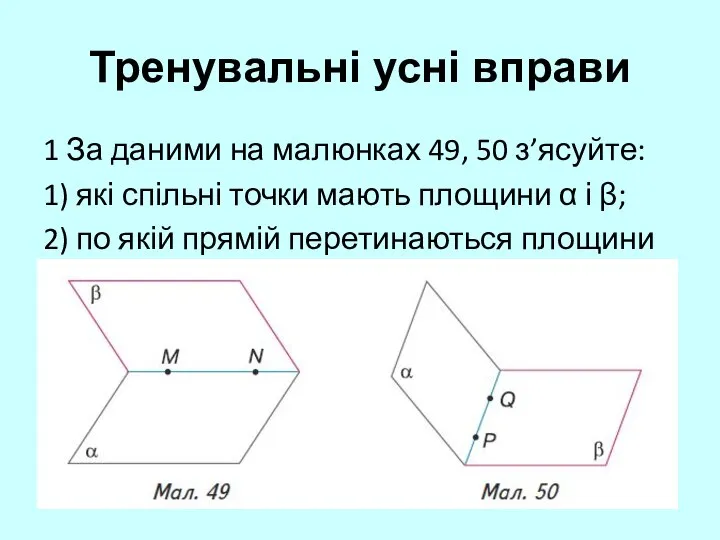
- 17. 1 За даними на малюнках 49, 50 з’ясуйте: 1) які спільні точки мають площини α і
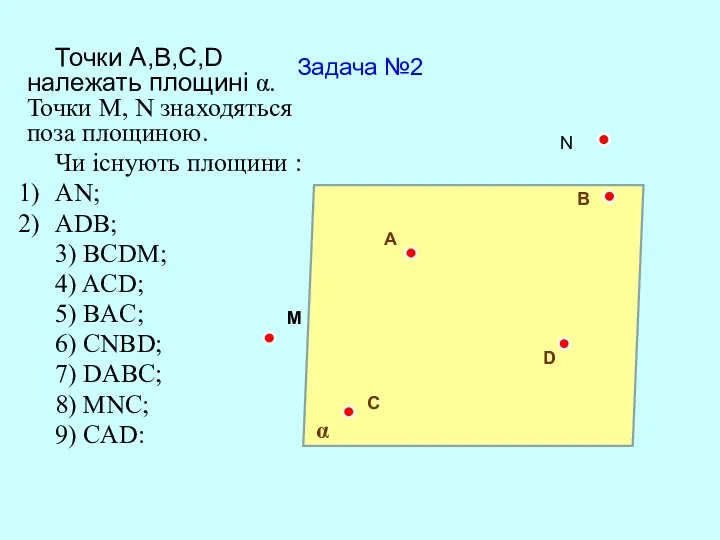
- 18. Задача №2 Точки A,B,C,D належать площині α. Точки M, N знаходяться поза площиною. Чи існують площини
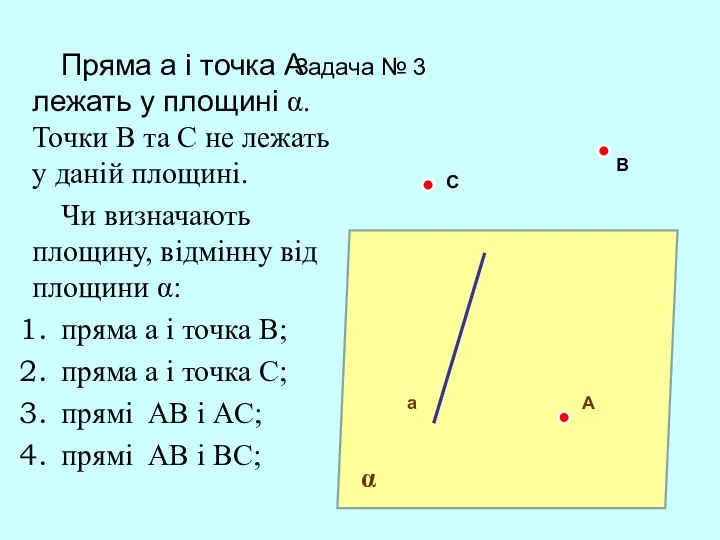
- 19. Пряма а і точка А лежать у площині α. Точки B та C не лежать у
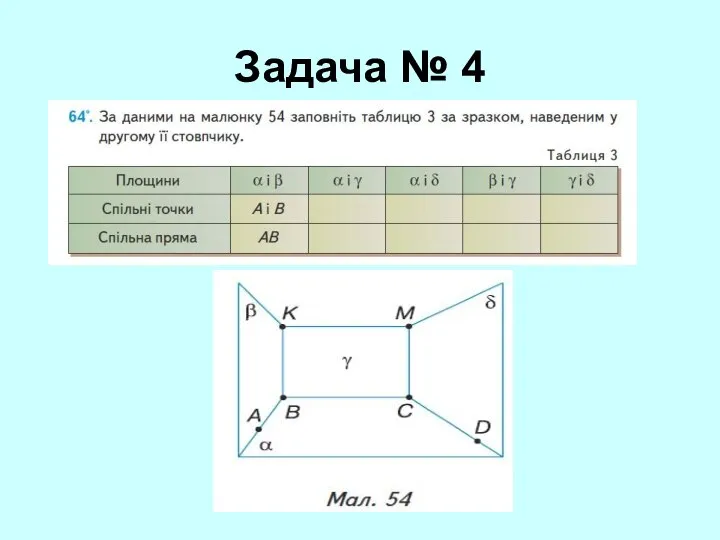
- 20. Задача № 4
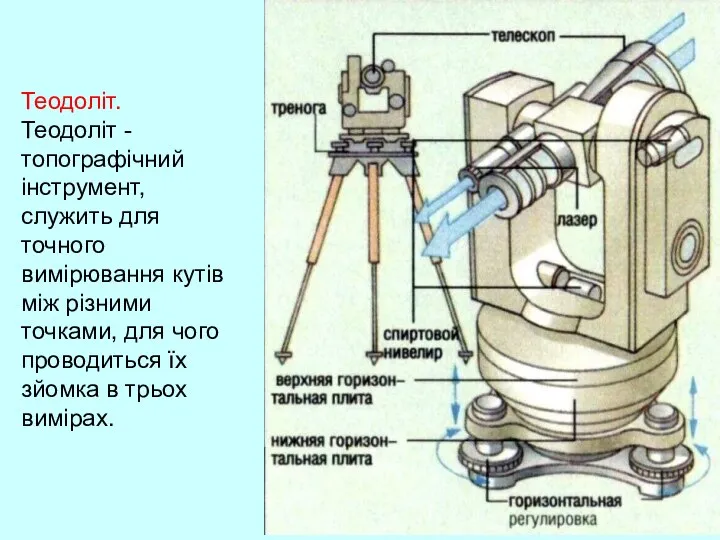
- 21. 77. Чому штативи багатьох приладів (фотоапарата, теодоліта тощо) виготовляють у формі триноги? Задачі практичного змісту Теодоліт
- 22. Теодоліт. Теодоліт - топографічний інструмент, служить для точного вимірювання кутів між різними точками, для чого проводиться
- 23. 78. Щоб перевірити, чи є дана поверхня плоскою, до неї прикладають лінійку в різних напрямах. Край
- 24. Аксіоми стереометрії в побуті, будівництві Триніжка для стійок. Тринога для лазерних рівнів Тринога кострова Пюпітр
- 26. Скачать презентацию




 Созвездия. Сималтиниус Раунд Тэйбл
Созвездия. Сималтиниус Раунд Тэйбл Суммы чисел
Суммы чисел Сфера
Сфера Методология нелинейного функционально - факторного моделирования природных и техногенных явлений
Методология нелинейного функционально - факторного моделирования природных и техногенных явлений Працюємо з відсотками і вирішуємо завдання
Працюємо з відсотками і вирішуємо завдання Многогранники
Многогранники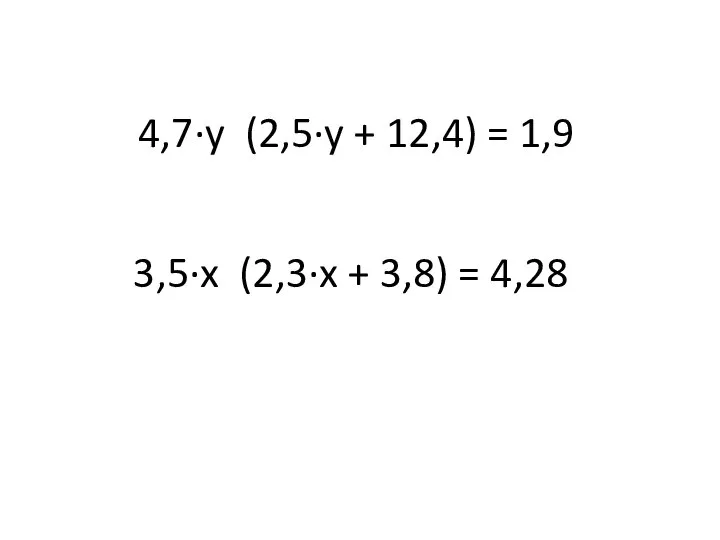 Учение о десятичных дробях
Учение о десятичных дробях Презентация на тему Арифметические действия с числами
Презентация на тему Арифметические действия с числами 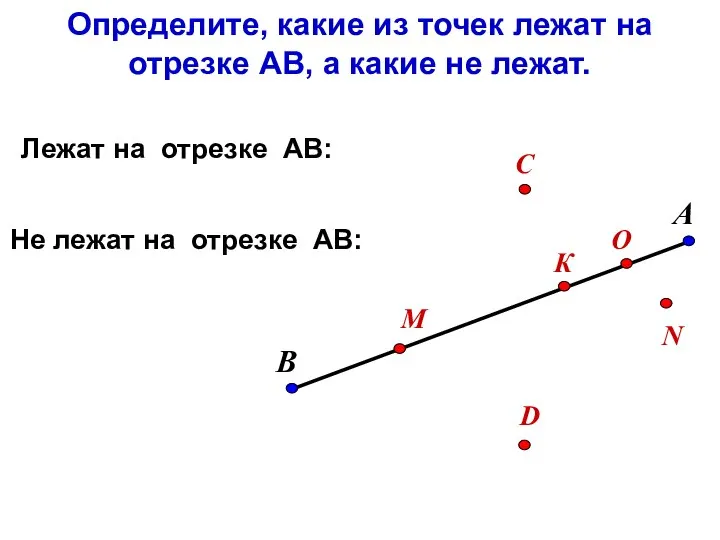 Отрезок. Длина отрезка
Отрезок. Длина отрезка Построение симметричных фигур
Построение симметричных фигур Презентация на тему Упрощение выражений 5 класс
Презентация на тему Упрощение выражений 5 класс  Уравнения высших степеней
Уравнения высших степеней Подготовка к ЕГЭ по математике
Подготовка к ЕГЭ по математике Перпендикуляр, наклонная, проекция наклонной
Перпендикуляр, наклонная, проекция наклонной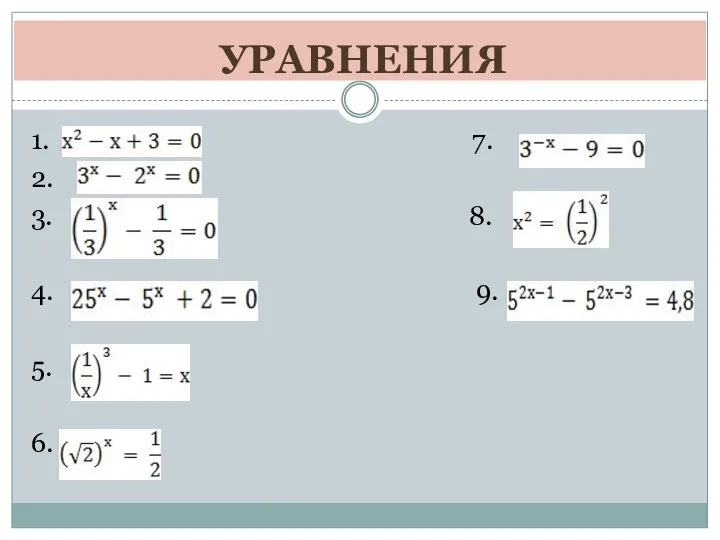 Решение показателей уравнений
Решение показателей уравнений Длина окружности и лощадь круга. Правила
Длина окружности и лощадь круга. Правила Правильные многогранники
Правильные многогранники Математика и статистика для анализа данных
Математика и статистика для анализа данных Спрощення виразів. Підготовка до ЗНО
Спрощення виразів. Підготовка до ЗНО Основные понятия математического анализа. Принятые обозначения числовых множеств
Основные понятия математического анализа. Принятые обозначения числовых множеств Проценты. Три задачи
Проценты. Три задачи Метод интервалов. Общий метод интервалов
Метод интервалов. Общий метод интервалов Засели числовые домики
Засели числовые домики Тема_5_2022
Тема_5_2022 Задачи и примеры по математике
Задачи и примеры по математике Метр. (2класс)
Метр. (2класс) Основные понятия комбинаторики. Факториал. Вычисление факториала
Основные понятия комбинаторики. Факториал. Вычисление факториала Преобразование логарифмических выражений
Преобразование логарифмических выражений