Содержание
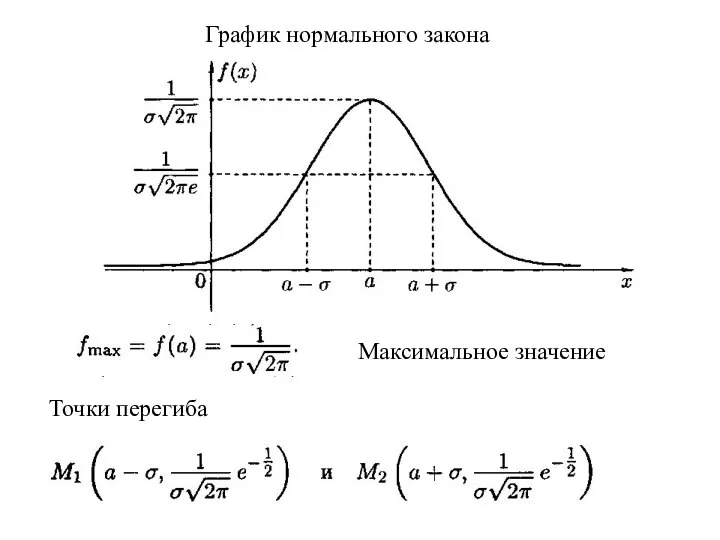
- 2. График нормального закона Максимальное значение Точки перегиба
- 3. Характеристическая функция гауссовской случайной величины
- 6. Пример. При сортировке случайные значения веса зерна распределены нормально со средним значением 0,15 г среднеквадратическим отклонением
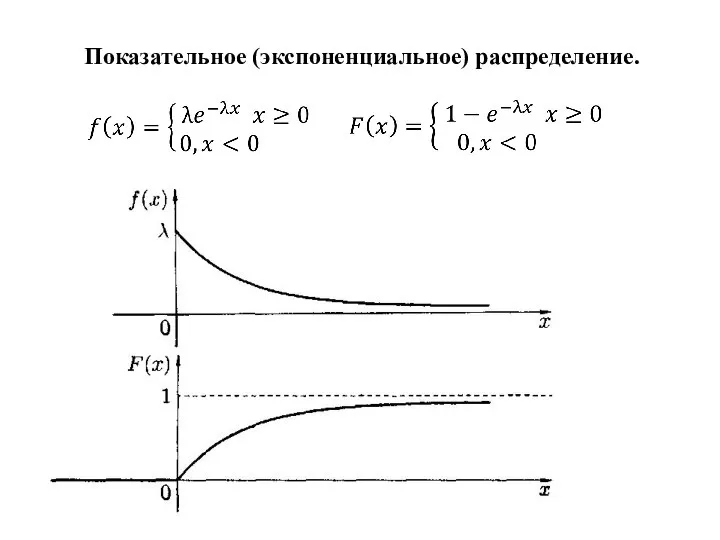
- 7. Показательное (экспоненциальное) распределение.
- 8. Характеристическая функция Кумулянтная функция
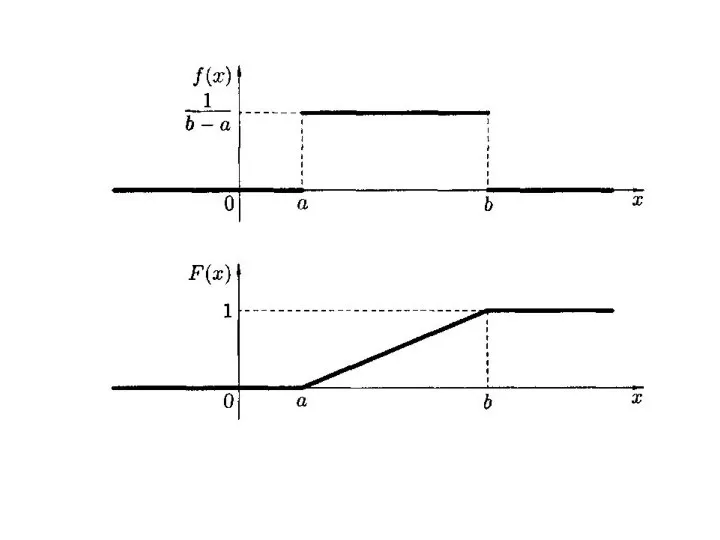
- 9. Равномерное распределение.
- 11. Распределение Пуассона Биномиальный закон распределения
- 12. Центральная предельная теорема
- 13. Основные понятия математической статистики Термин статистика происходит от латинского слова «статус»-состояние. В настоящее время статистика включает
- 14. 3. Разработка приемов статистического наблюдения и анализа статистических данных. Этот раздел составляет основное содержание математической статистики.
- 15. 3. Определение неизвестных параметров распределения. (Часто исходя из некоторых соображений можно сделать заключение о типе функции
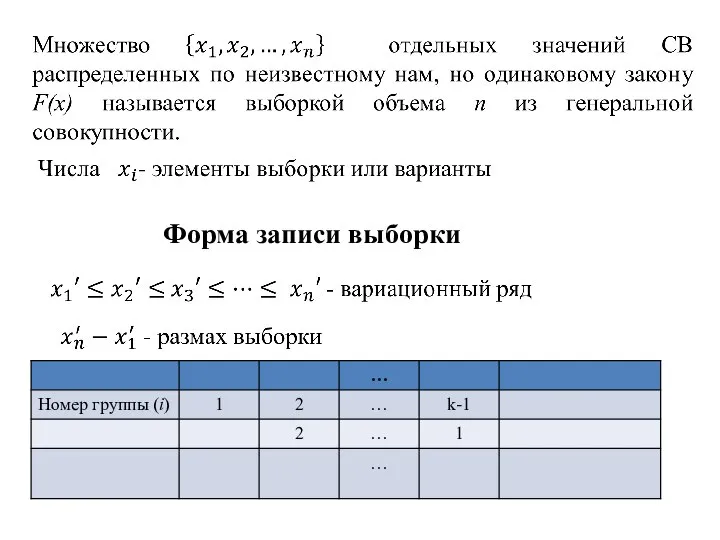
- 16. Требуется выяснить наличие функциональной или корреляционной связи между X и Y. Понятие выборки Определение. Совокупность всех
- 17. Форма записи выборки
- 18. Пример 1. При измерениях частоты пульса в однородных группах обследуемых получены следующие результаты: 71, 72, 74,
- 19. Полигон частот и полигон относительных частот
- 20. Пример 2. При измерениях роста в однородных группах обследуемых получены следующие результаты: 178, 160, 154, 183,
- 21. Исходные данные разобьем на 6 интервалов: [150,156), [156,162), [162,168), [168,174), [174,180), [180,186]
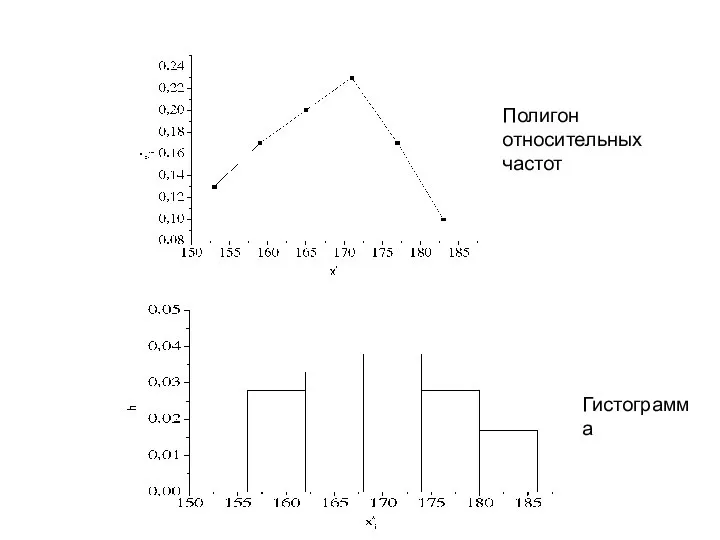
- 22. Гистограмма Полигон относительных частот
- 23. Эмпирическая функция распределения Определение. Характеристики СВ, найденные на основе выборочных данных называются эмпирическими или выборочными
- 26. L
- 27. Следствие1. (Теорема Бернулли). Пусть производится n независимых опытов, в каждом из которых может появиться некоторое событие
- 28. Оценки для неизвестных параметров закона распределения. Необходимо отметить, что любое значение искомого параметра, вычисленное на основе
- 30. Предъявим к оценке ряд требований, которым она должна удовлетворять, чтобы быть доброкачественной: 1. Оценка должна быть
- 33. Методы нахождения точечных оценок Наиболее распространенные методы построении точечных оценок: метод моментов, метод максимального правдоподобия метод
- 36. Предложенная оценка является состоятельной
- 37. Пример. При измерениях частоты пульса в однородных группах обследуемых получены следующие результаты: 71, 72, 74, 70,
- 38. Понятие интервального оценивания параметров. Доверительный интервал. Нахождение границ доверительного интервала
- 41. Критерий согласия Пирсона
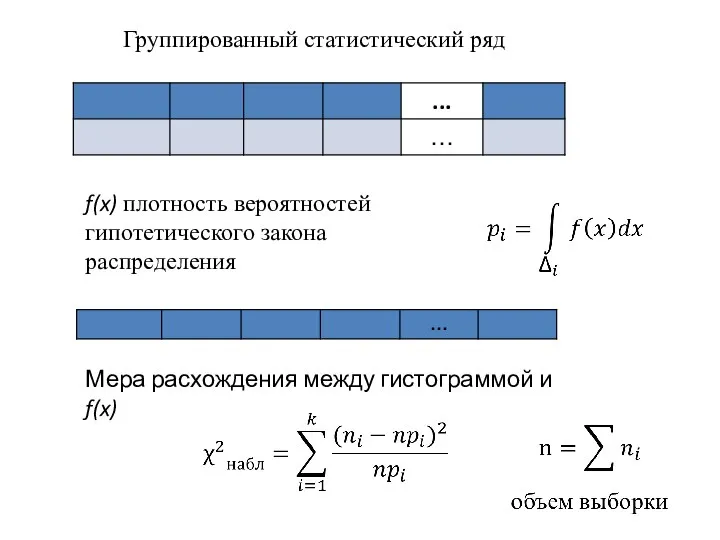
- 42. f(x) плотность вероятностей гипотетического закона распределения Группированный статистический ряд Мера расхождения между гистограммой и f(x)
- 45. Скачать презентацию















![Исходные данные разобьем на 6 интервалов: [150,156), [156,162), [162,168), [168,174), [174,180), [180,186]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1080513/slide-20.jpg)




















 Неопределённый и определённый интеграл
Неопределённый и определённый интеграл Выберите чётные числа (Использование триггеров в презентации)
Выберите чётные числа (Использование триггеров в презентации) Метод Гаусса
Метод Гаусса Решение систем уравнений графическим и аналитическим способом
Решение систем уравнений графическим и аналитическим способом Устное решение задач по готовым чертежам
Устное решение задач по готовым чертежам Презентация на тему Повторение курса начальной школы в 5-м классе
Презентация на тему Повторение курса начальной школы в 5-м классе  Проверочный тест 1 по геометрии
Проверочный тест 1 по геометрии Умножение одночлена на многочлен
Умножение одночлена на многочлен 1_urok_ponyatie_vektora
1_urok_ponyatie_vektora Параллельные прямые
Параллельные прямые Обобщение понятия о показателе степени
Обобщение понятия о показателе степени Вычисление производной
Вычисление производной Применение векторов к решению задач
Применение векторов к решению задач Решение сложных алгоритмических задач
Решение сложных алгоритмических задач Решение практико - ориентированных задач. Задачи про форматы листов
Решение практико - ориентированных задач. Задачи про форматы листов Геометрический смысл производной
Геометрический смысл производной Круг . Площадь круга
Круг . Площадь круга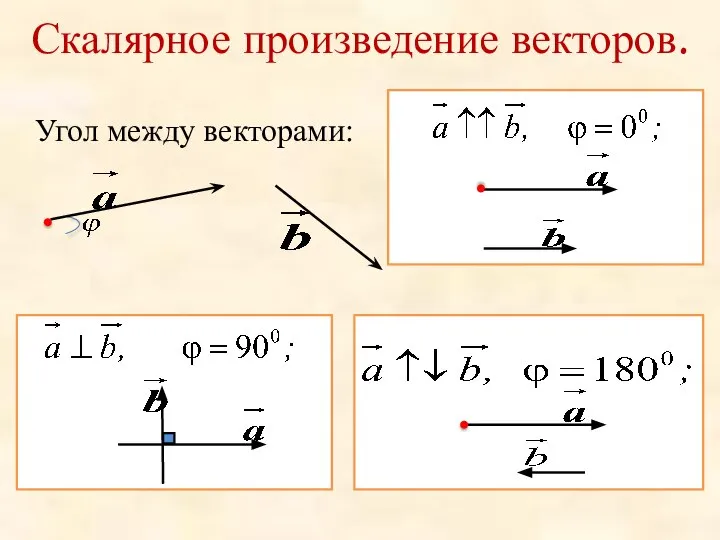 Скалярное произведение векторов
Скалярное произведение векторов Мы отправляемся в полёт
Мы отправляемся в полёт Умозаключения. Теоремы. Утверждения
Умозаключения. Теоремы. Утверждения Л11 Производная функции
Л11 Производная функции Решение уравнений с весной
Решение уравнений с весной Математический турнир Степень и ее свойства. 7 класс
Математический турнир Степень и ее свойства. 7 класс Руководитель кружка по математике для 7 класса
Руководитель кружка по математике для 7 класса Задачи на подсчет числа размещений, перестановок, сочетаний
Задачи на подсчет числа размещений, перестановок, сочетаний Четырехугольники
Четырехугольники Презентация на тему Уменьшаемое. Вычитаемое. Разность
Презентация на тему Уменьшаемое. Вычитаемое. Разность  Розбиття множини ОВ на групи
Розбиття множини ОВ на групи