Содержание
- 2. Определение №1 Функция y=f(x) называется непрерывной в точке х0, если выполнены условия: Непрерывность функций
- 3. Определение №1 Функция y=f(x) называется непрерывной в точке х0, если выполнены условия: Функция определена в точке
- 4. Определение №1 Функция y=f(x) называется непрерывной в точке х0, если выполнены условия: Функция определена в точке
- 5. Определение №1 Функция y=f(x) называется непрерывной в точке х0, если выполнены условия: Функция определена в точке
- 6. Определение Функция y=f(x) называется непрерывной в точке х0 справа (слева), если выполнены условия: Функция определена в
- 7. Определение Функция y=f(x) называется непрерывной в точке х0 справа (слева), если выполнены условия: Функция определена в
- 8. Определение №2 Если существуют конечные левый и правый пределы, равные между собой и равные значению функции
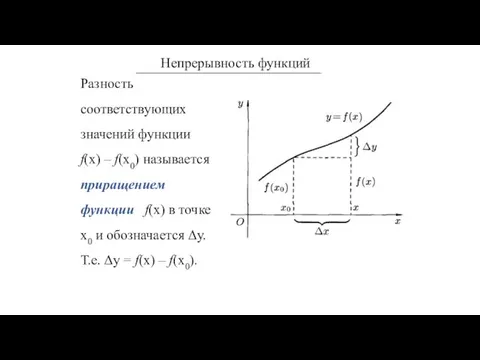
- 9. Пусть функция у = f(x) определена в некотором интервале (a;b). Возьмем произвольную точку x0 ϵ (a;b).
- 10. Пусть функция у = f(x) определена в некотором интервале (a;b). Возьмем произвольную точку x0 ϵ (a;b).
- 11. Разность соответствующих значений функции f(x) – f(x0) называется приращением функции f(х) в точке х0 и обозначается
- 12. Определение №3 Функция y=f(x) называется непрерывной в точке х0 , если ее приращение в этой точке
- 13. Теорема Если функции f(x) и g(x) непрерывны в точке х0 , то их сумма, разность, произведение
- 14. Теорема Если функции f(x) и g(x) непрерывны в точке х0 , то их сумма, разность, произведение
- 15. Теорема Если функция g(x) непрерывна в точке х0, а функция f(g) непрерывна в точке g0, причем
- 16. Теорема Если функция f(x) имеет обратную функцию f -1(у) и непрерывна в точке х0, то функция
- 17. Теорема Всякая элементарная функция непрерывна в каждой точке, в которой она определена. Свойства функций, непрерывных в
- 18. Теорема Всякая элементарная функция непрерывна в каждой точке, в которой она определена. Доказательство: Пусть f(x) =
- 19. Пусть f(x) = sinx. Докажем, что функция непрерывна в любой точке х0. Свойства функций, непрерывных в
- 20. Пусть f(x) = sinx. Докажем, что функция непрерывна в любой точке х0. Свойства функций, непрерывных в
- 21. Пусть f(x) = sinx. Докажем, что функция непрерывна в любой точке х0. Свойства функций, непрерывных в
- 22. Пусть f(x) = sinx. Докажем, что функция непрерывна в любой точке х0. Свойства функций, непрерывных в
- 23. Пусть f(x) = еx. Докажем, что функция непрерывна в любой точке х0. Свойства функций, непрерывных в
- 24. Пусть f(x) = еx. Докажем, что функция непрерывна в любой точке х0. Свойства функций, непрерывных в
- 25. Пусть f(x) = еx. Докажем, что функция непрерывна в любой точке х0. Свойства функций, непрерывных в
- 26. Свойства функций, непрерывных в точке
- 27. Точки разрыва функции и их классификация
- 28. Определение Точки, в которых нарушается условие непрерывности функции называются точками разрыва этой функции. Точки разрыва функции
- 29. Определение Точка разрыва х0 называется точкой разрыва первого рода функции y=f(x), если в этой точке существуют
- 30. Определение Точка разрыва х0 называется точкой разрыва первого рода функции y=f(x), если в этой точке существуют
- 31. Определение Точка разрыва х0 называется точкой разрыва первого рода функции y=f(x), если в этой точке существуют
- 32. Определение Точка разрыва х0 называется точкой разрыва второго рода функции y=f(x), если в этой точке хотя
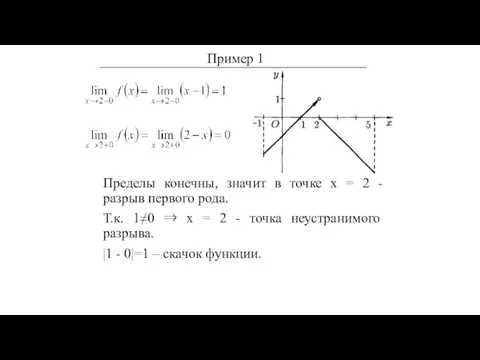
- 33. Исследовать на непрерывность функцию Пример 1
- 34. Исследовать на непрерывность функцию Найдем односторонние пределы в точке х = 2: Пример 1
- 35. Исследовать на непрерывность функцию Найдем односторонние пределы в точке х=2: Пример 1
- 36. Исследовать на непрерывность функцию Найдем односторонние пределы в точке х=2: Пример 1
- 37. Пределы конечны, значит в точке х = 2 - разрыв первого рода. Т.к. 1≠0 ⇒ х
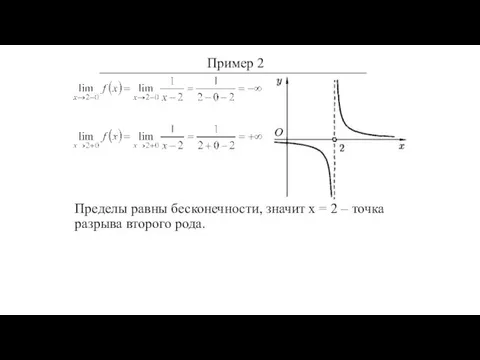
- 38. Исследовать на непрерывность функцию Пример 2
- 39. Исследовать на непрерывность функцию Найдем односторонние пределы в точке х=2: Пример 2
- 40. Исследовать на непрерывность функцию Найдем односторонние пределы в точке х=2: Пример 2
- 41. Пределы равны бесконечности, значит х = 2 – точка разрыва второго рода. Пример 2
- 42. Свойства функций, непрерывных на отрезке
- 43. Определение Функция у = f(x) называется непрерывной на интервале (a;b), если она непрерывна в каждой точке
- 44. Определение Функция у = f(x) называется непрерывной на отрезке [a;b], если она непрерывна на интервале (a;b)
- 45. Теорема Вейерштрасса Всякая непрерывная на отрезке [a;b] функция ограничена на нем и достигает на этом отрезке
- 46. Теорема Вейерштрасса Всякая непрерывная на отрезке [a;b] функция ограничена на нем и достигает на этом отрезке
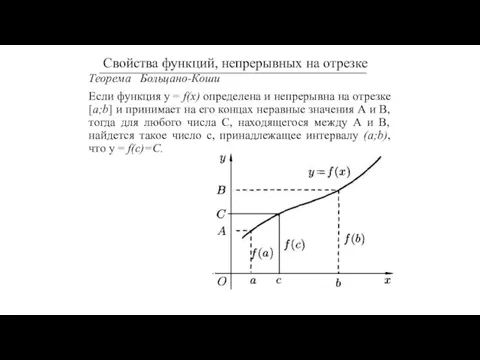
- 47. Теорема Больцано-Коши Если функция у = f(x) определена и непрерывна на отрезке [a;b] и принимает на
- 48. Теорема Больцано-Коши Если функция у = f(x) определена и непрерывна на отрезке [a;b] и принимает на
- 49. Следствие Если функция у = f(x) непрерывна на отрезке [a;b] и принимает на его концах значения
- 51. Скачать презентацию







































![Определение Функция у = f(x) называется непрерывной на отрезке [a;b], если она](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/862447/slide-43.jpg)
![Теорема Вейерштрасса Всякая непрерывная на отрезке [a;b] функция ограничена на нем и](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/862447/slide-44.jpg)
![Теорема Вейерштрасса Всякая непрерывная на отрезке [a;b] функция ограничена на нем и](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/862447/slide-45.jpg)

![Следствие Если функция у = f(x) непрерывна на отрезке [a;b] и принимает](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/862447/slide-48.jpg)
 Определенный интеграл
Определенный интеграл Цилиндр. История возникновения
Цилиндр. История возникновения Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика
Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика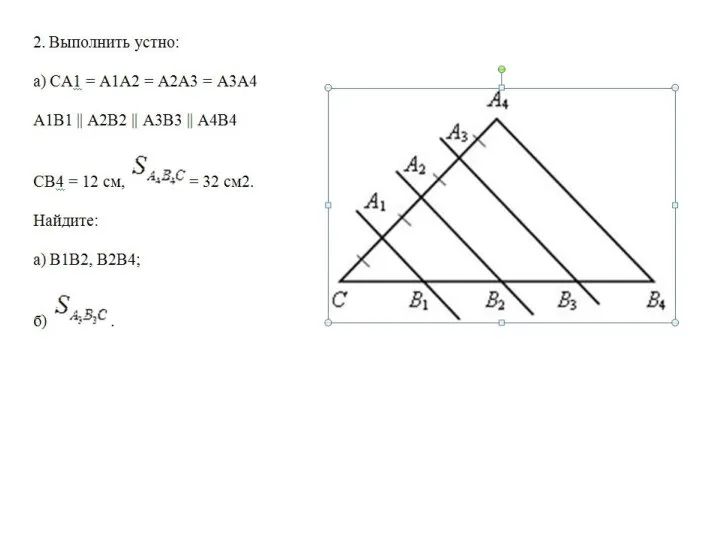 Признаки подобия треугольников. Урок 31
Признаки подобия треугольников. Урок 31 Приложения Определенного интеграла
Приложения Определенного интеграла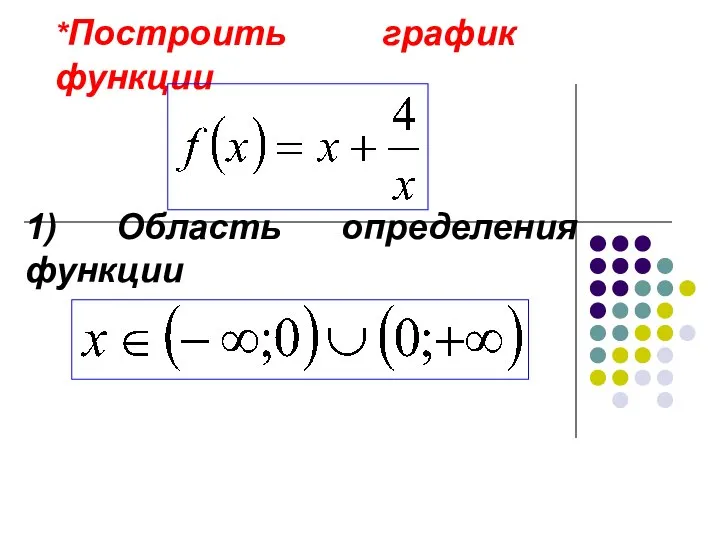 Построение графиков функций
Построение графиков функций Презентация на тему ОТЫСКАНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ
Презентация на тему ОТЫСКАНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ  Евклидовы пространства
Евклидовы пространства Среднее арифметическое. Размах. Мода
Среднее арифметическое. Размах. Мода Параллельность плоскостей
Параллельность плоскостей Обыкновенные дифференциальные уравнения первого порядка. Задача и теорема Коши. Общее и частное решения
Обыкновенные дифференциальные уравнения первого порядка. Задача и теорема Коши. Общее и частное решения Метод составления уравнений неголономной механики в задаче волнового твердотельного гироскопа
Метод составления уравнений неголономной механики в задаче волнового твердотельного гироскопа Сложение десятичных дробей
Сложение десятичных дробей Рюкзак. Восстановление ответа
Рюкзак. Восстановление ответа Дискриминантный анализ Фишера с kernel trick
Дискриминантный анализ Фишера с kernel trick Степень числа
Степень числа Математическая викторина
Математическая викторина Геометрический конструктор GeoGebra
Геометрический конструктор GeoGebra Тригонометрия. Математическая игра АС-11
Тригонометрия. Математическая игра АС-11 Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Как математика учит критическому мышлению
Как математика учит критическому мышлению Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы Шарады, метаграммы, логогрифы
Шарады, метаграммы, логогрифы Определение высоты дерева
Определение высоты дерева 12. Тэтраэдр
12. Тэтраэдр Знакомимся с многоугольниками
Знакомимся с многоугольниками Профессия математик - инновационные сферы применения знаний Исследователь: ученик 10 класса Романенко Николай Руководитель: уч
Профессия математик - инновационные сферы применения знаний Исследователь: ученик 10 класса Романенко Николай Руководитель: уч Делениес остатком
Делениес остатком