Содержание
- 2. Цели урока: Рассмотреть общие методы решения уравнений. Научиться применять эти методы при решении уравнений. Формировать навыки
- 3. Рассмотрим уравнения: 1) х² - 2 х = 0; 2) sin²x + sinx = 0; 3)
- 4. Рассмотрим уравнения:
- 5. Общие методы решения уравнений: Замена уравнения h(f(x)) = h(g(x)) уравнением f(x) = g(x). Метод разложения на
- 6. Этот метод мы применяем: при решении показательных уравнений, когда переходили от уравнения (а>0, а≠1) к уравнению
- 7. Пример 1: Решить уравнение Ответ: 0; 1,5.
- 8. Пример 2:
- 9. Уравнение f(x)g(x)h(x) = 0 можно заменить совокупностью уравнений: Решив уравнения этой совокупности, нужно взять те их
- 10. Пример 3: Решить уравнение
- 11. Из найденных корней этой системе неравенств удовлетворяет только х = 9, остальные являются посторонними для данного
- 12. Если уравнение f(x)= 0 удалось преобразовать к виду p(g(x)) = 0, то нужно ввести новую переменную
- 13. Пример 4: Решить уравнение Введём новую переменную . Получим: Освободившись от знаменателей, получим:
- 14. Пример 4: Найдём корни квадратного уравнения: Выполним проверку корней на выполнение условия: 5(у – 3)(у +
- 15. Пример 4: Вернёмся к замене переменной и решим два уравнения: и Ответ:
- 16. 3. Функционально-графический метод. Чтобы графически решить уравнение f(x) = g(x) нужно построить графики функций у =
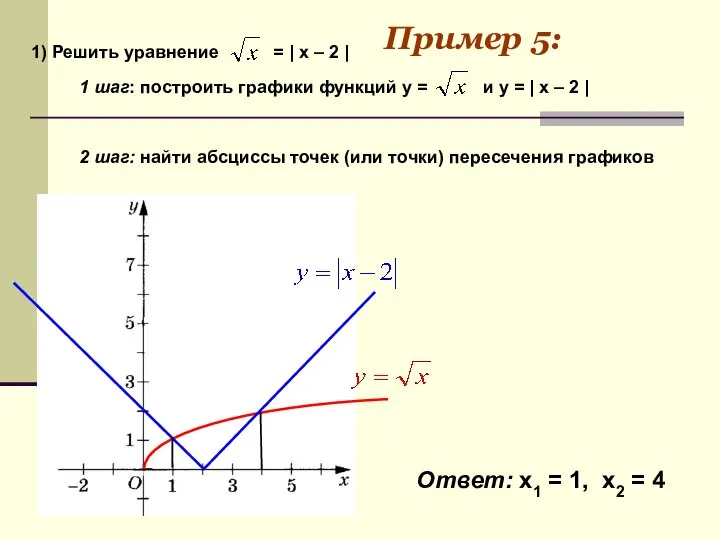
- 17. 2 шаг: найти абсциссы точек (или точки) пересечения графиков Ответ: x1 = 1, х2 = 4
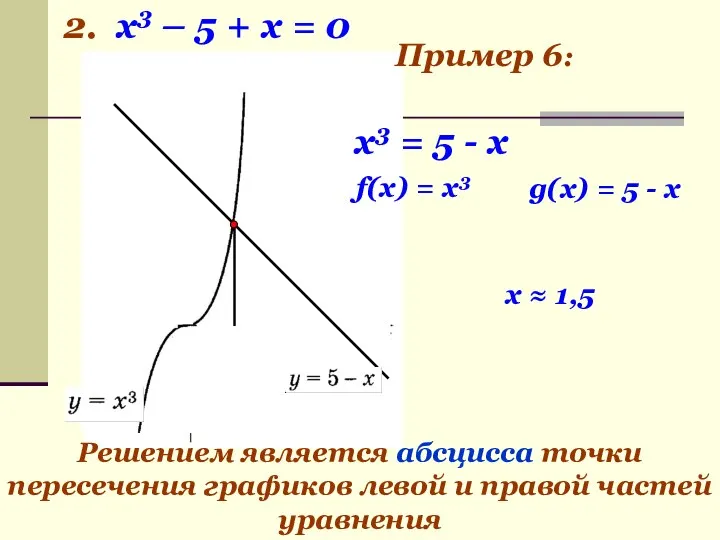
- 18. 2. x3 – 5 + х = 0 g(x) = 5 - х f(x) = х3
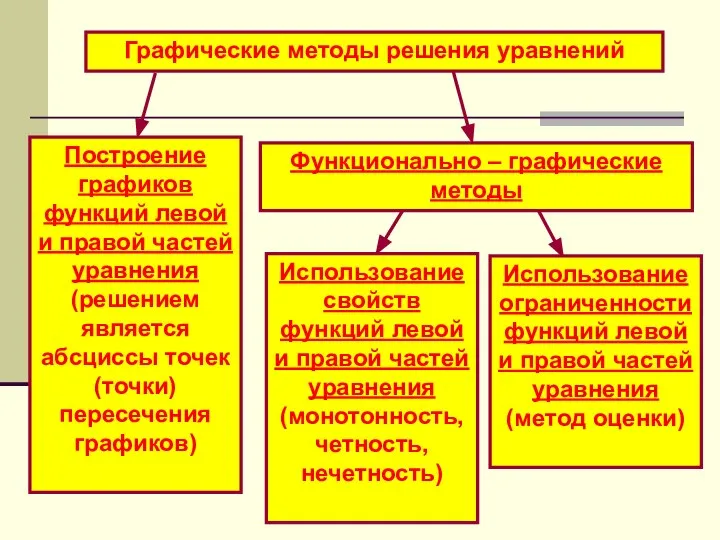
- 19. Графические методы решения уравнений Построение графиков функций левой и правой частей уравнения (решением является абсциссы точек
- 20. Рассмотрим функцию у = х² - 2х + 2. Её графиком является парабола, ветви которой направлены
- 21. Для функции у = х² - 2х + 2 Функция у = cos 2πx обладает свойством:
- 22. х² - 2х + 2 = 1, cos 2πx = 1. Решив 1 уравнение получили: х
- 23. Мы рассмотрели общие методы решения уравнений, примеры применения этих методов. Перейдём к практической работе. Решаем №
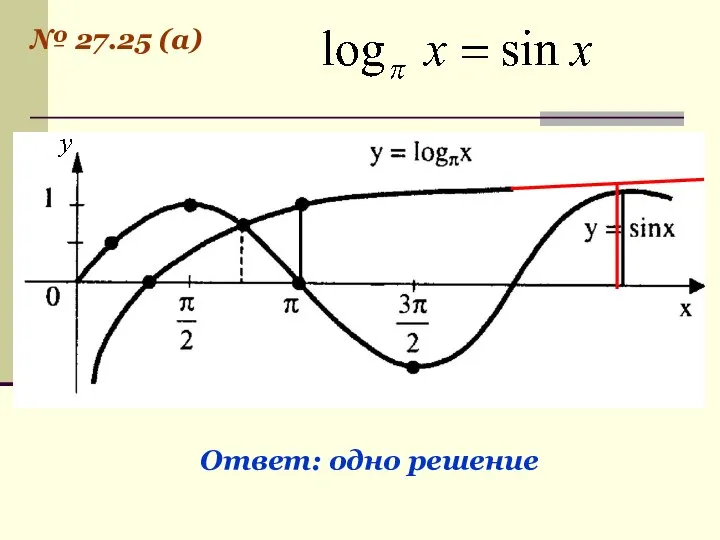
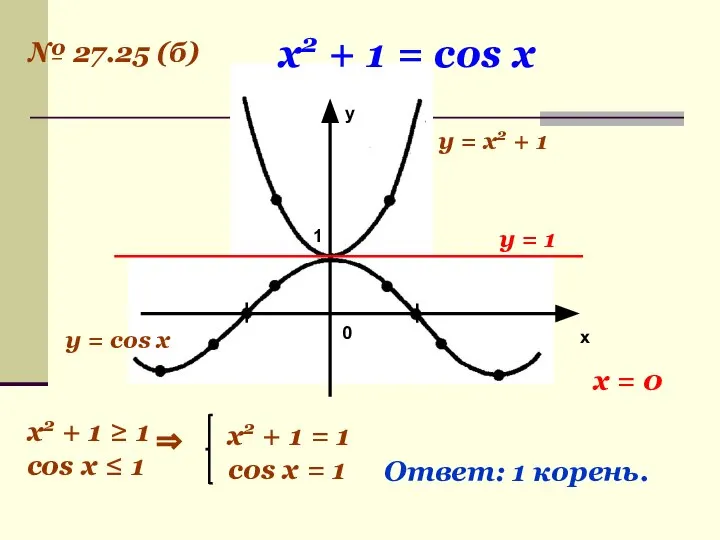
- 24. № 27.25 (а) Ответ: одно решение
- 25. 1 0 х у x2 + 1 = cos x y = x2 + 1 y
- 27. Скачать презентацию



















 Презентация на тему Геометрическая прогрессия и ее свойство
Презентация на тему Геометрическая прогрессия и ее свойство  Трикутники
Трикутники Перпендикуляр и наклонная к плоскости. Решение задач
Перпендикуляр и наклонная к плоскости. Решение задач Презентация на тему Иррациональные числа (8 класс)
Презентация на тему Иррациональные числа (8 класс)  Тригонометрия. Математическая игра АС-11
Тригонометрия. Математическая игра АС-11 Презентация на тему Сдвиг графика функции y = x вдоль осей координат
Презентация на тему Сдвиг графика функции y = x вдоль осей координат  Отображение. Отражение относительно прямой. Преобразование единичного квадрата
Отображение. Отражение относительно прямой. Преобразование единичного квадрата Решение задач
Решение задач Старинные меры массы и длины
Старинные меры массы и длины Скалярное произведение векторов
Скалярное произведение векторов Волшебный треугольник
Волшебный треугольник Тела вращения
Тела вращения Равнобедренный треугольник
Равнобедренный треугольник Пифагор и литература
Пифагор и литература Решение примеров и простых задач в пределах 10
Решение примеров и простых задач в пределах 10 Заниматика. Миром управляют числа
Заниматика. Миром управляют числа Случайные процессы с дискретными состояниями
Случайные процессы с дискретными состояниями Параллельные прямые
Параллельные прямые Lecture 6. Techniques of Integration (part 1)
Lecture 6. Techniques of Integration (part 1) Аналитическая панель
Аналитическая панель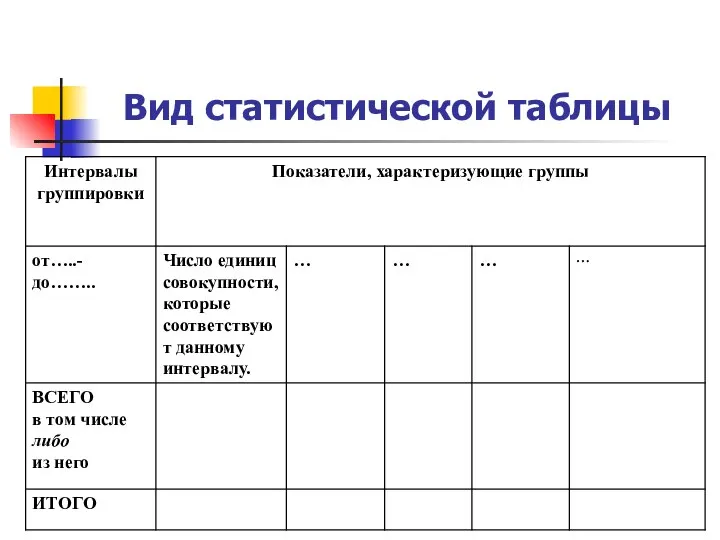 Вид статистической таблицы
Вид статистической таблицы Случаи сложения вида +7
Случаи сложения вида +7 Усеченная пирамида
Усеченная пирамида График равномерного движения
График равномерного движения Задачи на проценты. Схемы
Задачи на проценты. Схемы Многогранники в нашей жизни
Многогранники в нашей жизни Прямоугольный параллелепипед. Урок обобщения и систематизации знаний
Прямоугольный параллелепипед. Урок обобщения и систематизации знаний Презентация на тему Комбинации шара с многогранниками и фигурами вращения
Презентация на тему Комбинации шара с многогранниками и фигурами вращения