Решение задачи диффузии

Решение задачи диффузии
Граничные условия могут быть
Поток пропорционален градиенту давления
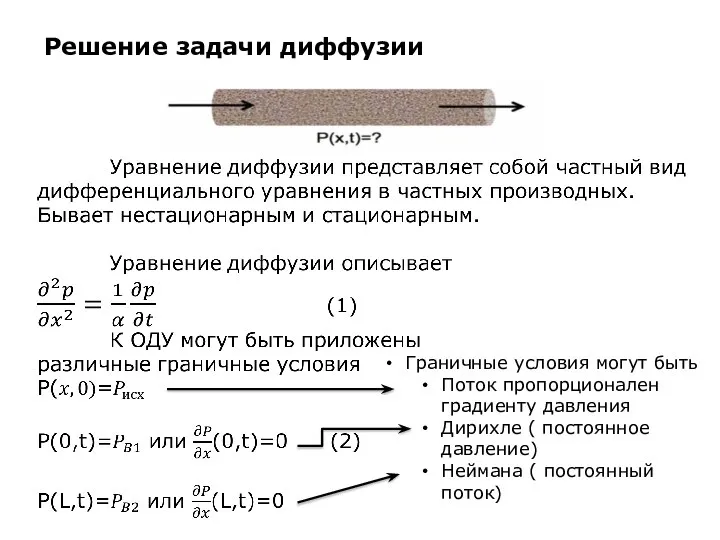
Дирихле ( постоянное давление)
Неймана ( постоянный поток)

Уравнение диффузии

Граничные условия Дирихле и Неймана
Условие Дирихле, применённое к обыкновенным дифференциальным уравнениям или к дифференциальным уравнениям в частных производных, определяет поведение системы на границе области.
В дифференциальных уравнениях краевая задача Неймана с заданными граничными условиями для производной искомой функции на границе области — так называемые граничные условия второго рода.

Использования ряда Тейлора для производной
Для аппроксимации функции многочленами используем ряд Тейлора:

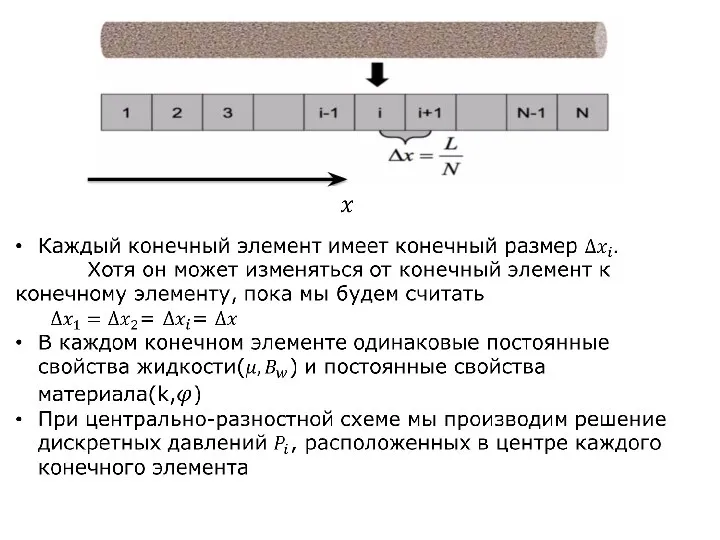
Замена конечно разностной аппроксимации в каждом конечном элементе

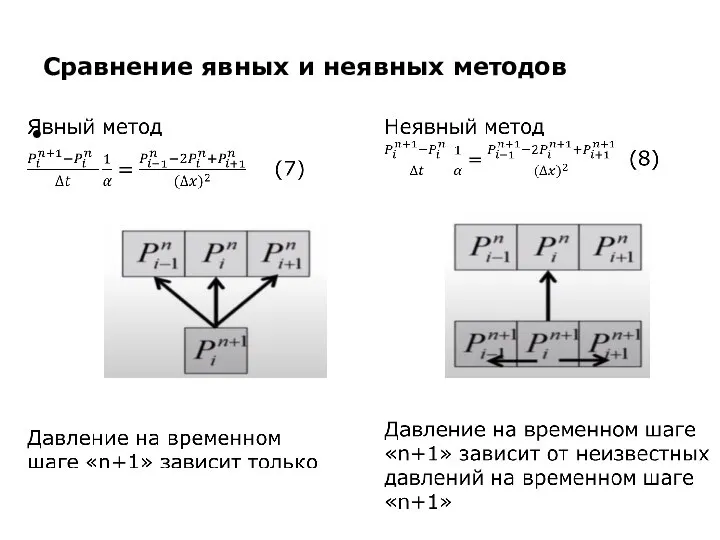
Сравнение явных и неявных методов

Неявный метод

Неявный метод

Граничные условия

Граничные условия Дирихле

Граничные условия Неймана