Слайд 2Цели занятия:
научить решать дифференциальные уравнения;
научить применять дифференциальные уравнения к решению задач с

медицинским содержанием;
провести контроль практических умений по теме: «Обыкновенные дифференциальные уравнения»
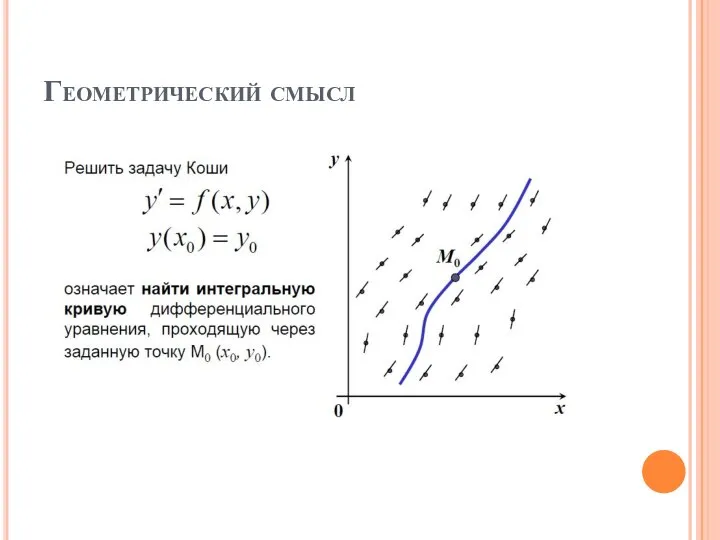
Слайд 4Порядок дифференциального уравнения

Слайд 11Алгоритм решения ДУ
Уединить производную (перенести ее в левую часть равенства).
Заменить на .
Разделить

переменные.
Проинтегрировать обе части уравнения.
По начальным условиям определить значение константы.
Слайд 22Популяция бактерий x(t) растет так, что скорость ее роста в момент времени

t (t - часы) равна одной десятой от размера популяции. Описать этот процесс роста дифференциальным уравнением. Чему равен размер популяции спустя 10 часов, если начальное условие х(0) = 1000?
















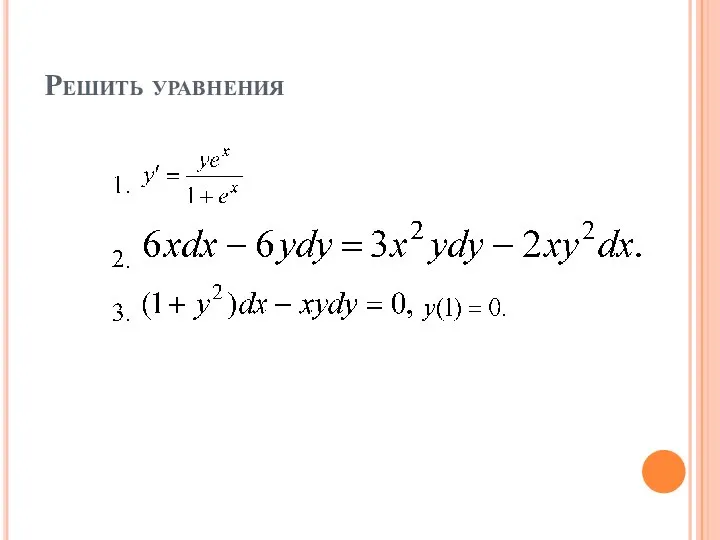




 Стандартизация в различных сферах. Сущность стандартизации
Стандартизация в различных сферах. Сущность стандартизации Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Презентация на тему Комплексные числа 11 класс
Презентация на тему Комплексные числа 11 класс  Ряды
Ряды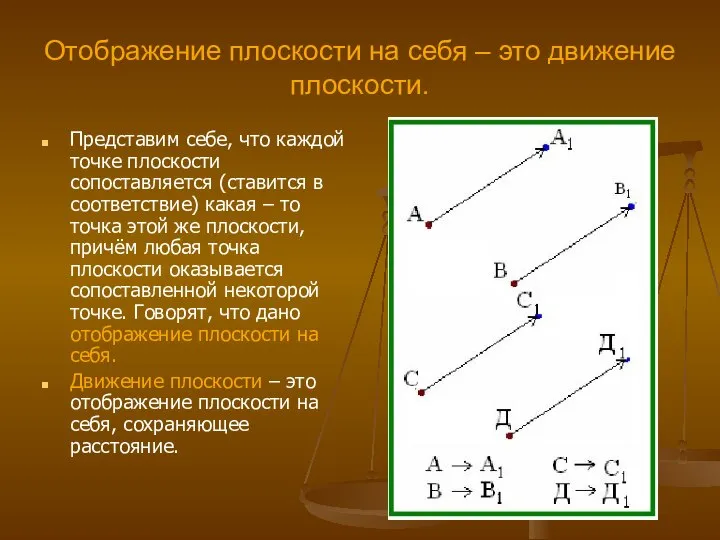 Геометрические преобразования плоскости
Геометрические преобразования плоскости Интерактивная игра Геометрические фигуры
Интерактивная игра Геометрические фигуры Параллелепипед
Параллелепипед Презентация на тему Тетраэдр, виды сечений и решение задач по тетраэдру
Презентация на тему Тетраэдр, виды сечений и решение задач по тетраэдру  слож и выч вект умножение на число
слож и выч вект умножение на число Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Задачи с величинами: цена, количество, стоимость
Задачи с величинами: цена, количество, стоимость Методы оптимальных решений
Методы оптимальных решений Deterministic finite automata. Nondeterministic finite automata
Deterministic finite automata. Nondeterministic finite automata Презентация на тему Измерение углов (7 класс)
Презентация на тему Измерение углов (7 класс)  ДМ.9. Замкнутые классы
ДМ.9. Замкнутые классы Задачи на построение
Задачи на построение Төзек күпкырлыклар
Төзек күпкырлыклар Математика. 1 класс
Математика. 1 класс Пределы и непрерывность. Предел функции
Пределы и непрерывность. Предел функции Задания по математике (5 класс, часть 5)
Задания по математике (5 класс, часть 5) Знакомство с линиями чертежа Замкнутая, незамкнутая
Знакомство с линиями чертежа Замкнутая, незамкнутая Викторина по математике, 1 класс
Викторина по математике, 1 класс Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях
Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях Элементы комбинаторики
Элементы комбинаторики Случаи вычитания 12 -
Случаи вычитания 12 - Начальные геометрические сведения. Признаки равенства треугольников
Начальные геометрические сведения. Признаки равенства треугольников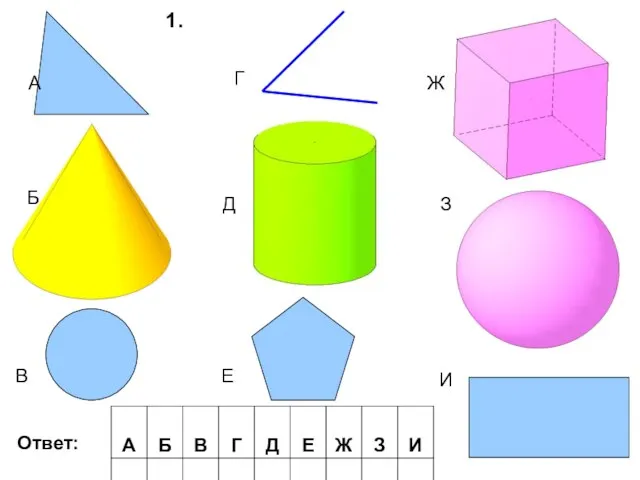 Геометрические тела. 5 класс
Геометрические тела. 5 класс Числа второго десятка
Числа второго десятка