Презентация на тему Расстояние от точки до плоскости

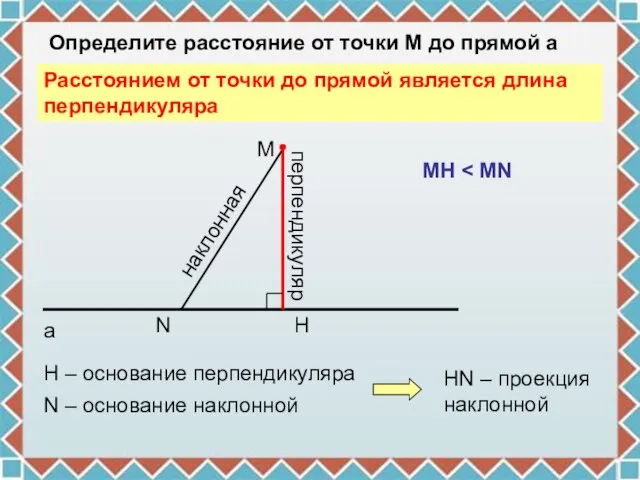
N
H
M
a
Определите расстояние от точки М до прямой а
перпендикуляр
Н – основание перпендикуляра
наклонная
N – основание наклонной
HN – проекция наклонной
Расстоянием от точки до прямой является длина перпендикуляра
MH < MN

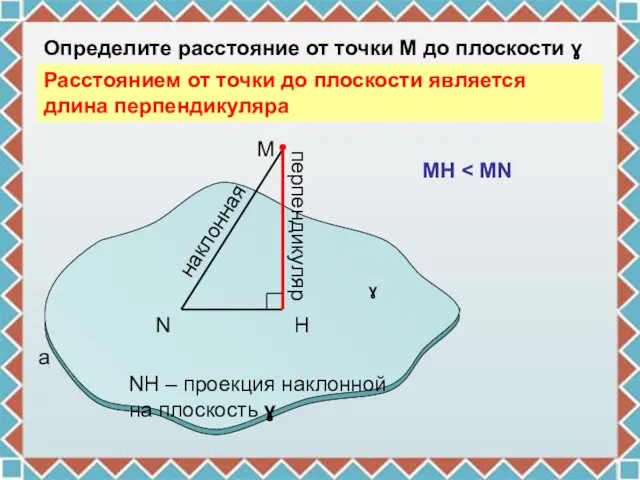
N
H
M
a
перпендикуляр
наклонная
Определите расстояние от точки М до плоскости ɣ
ɣ
NH – проекция наклонной на плоскость ɣ
MH < MN
Расстоянием от точки до плоскости является длина перпендикуляра

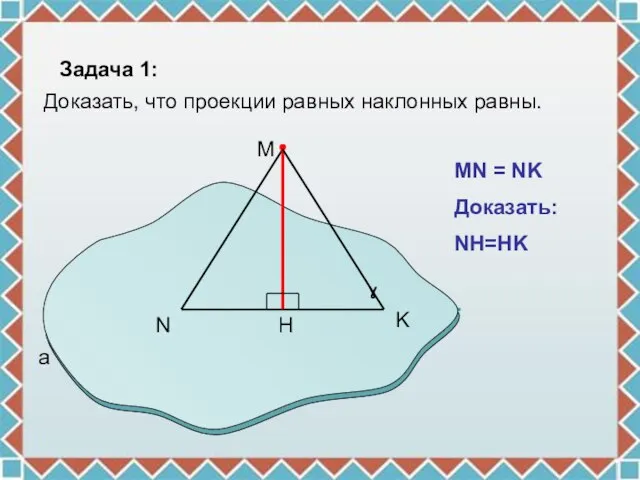
N
H
M
a
ɣ
MN = NK
Доказать:
NH=HK
Задача 1:
Доказать, что проекции равных наклонных равны.
K

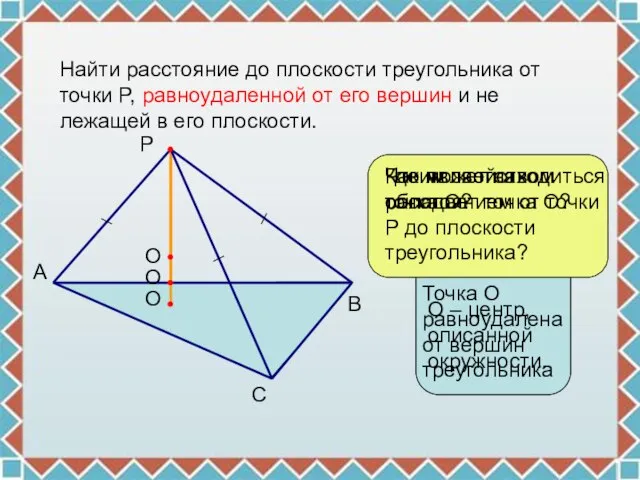
Найти расстояние до плоскости треугольника от точки P, равноудаленной от его вершин и не лежащей в его плоскости.
P
A
B
C
Что является расстоянием от точки Р до плоскости треугольника?
О
О
О
Где может находиться точка О?
Каким свойством обладает точка О?
Точка О равноудалена от вершин треугольника
О – центр, описанной окружности.

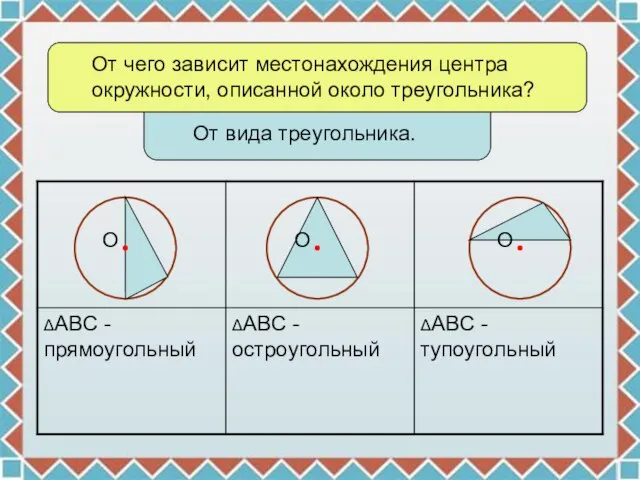
От чего зависит местонахождения центра окружности, описанной около треугольника?
От вида треугольника.
О
О
О

План решения задачи:
Определить вид треугольника и местонахождение точки О.
Найти радиус описанной окружности.
ΔАВС
3. По теореме Пифагора найти расстояние РО

Задача 2:
Ответ:
Ответ: