Содержание
- 2. -algebras *-homomorphism Algebraic Quantum Field Theory (AQFT). Tools
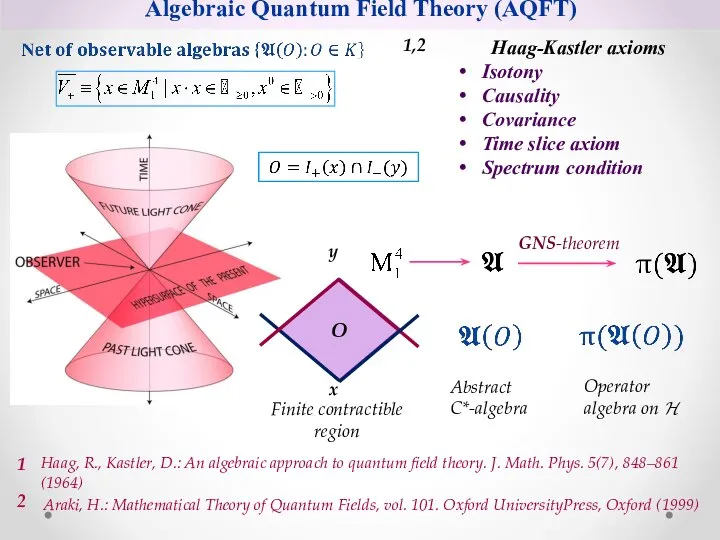
- 4. Algebraic Quantum Field Theory (AQFT) Haag-Kastler axioms Isotony Causality Covariance Time slice axiom Spectrum condition 1,2
- 5. Algebraic Quantum Field Theory (AQFT) Isotony Haag-Kastler axioms
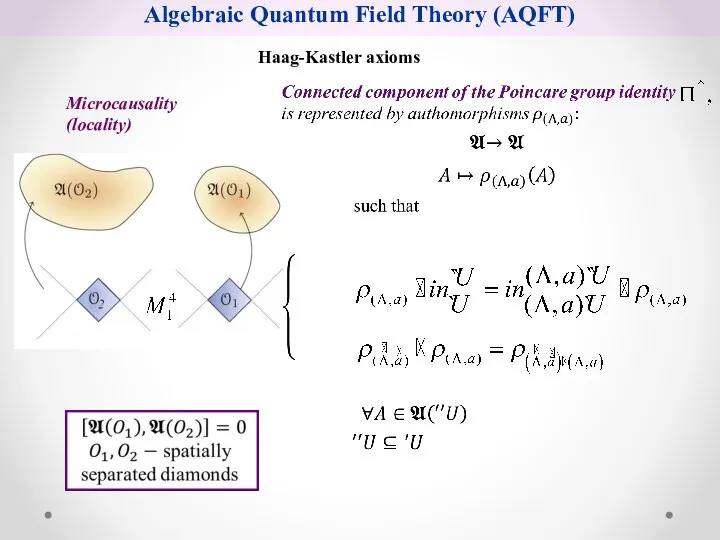
- 6. Microcausality (locality) Algebraic Quantum Field Theory (AQFT) Haag-Kastler axioms
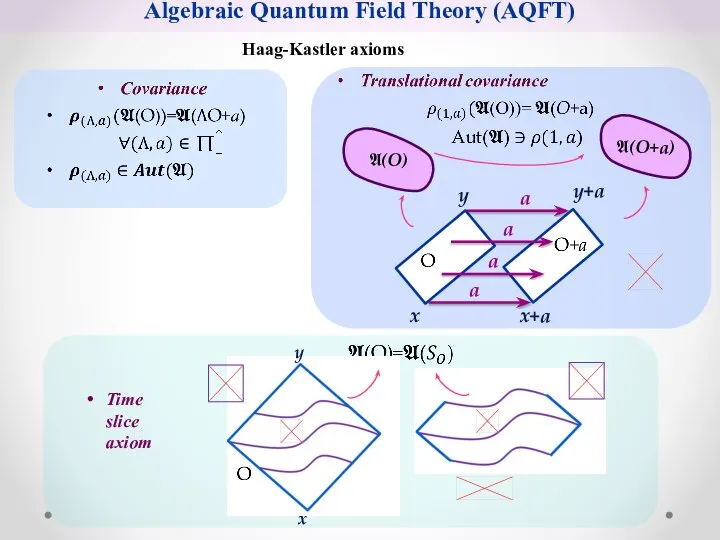
- 7. Algebraic Quantum Field Theory (AQFT) Haag-Kastler axioms
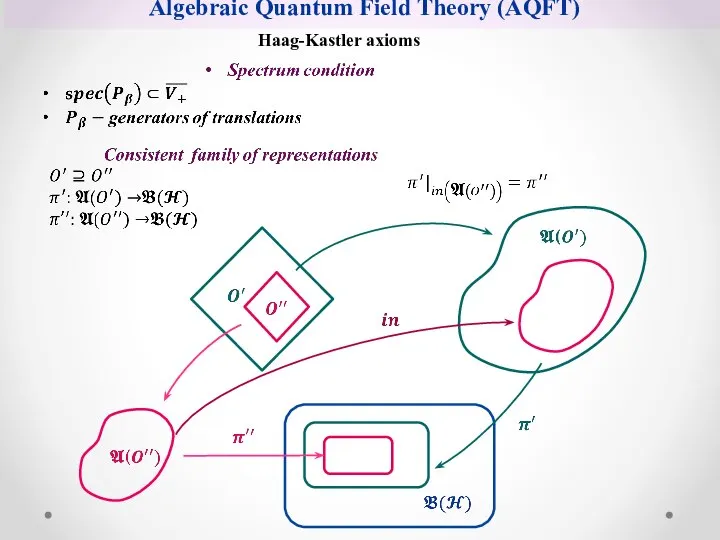
- 8. Algebraic Quantum Field Theory (AQFT) Haag-Kastler axioms
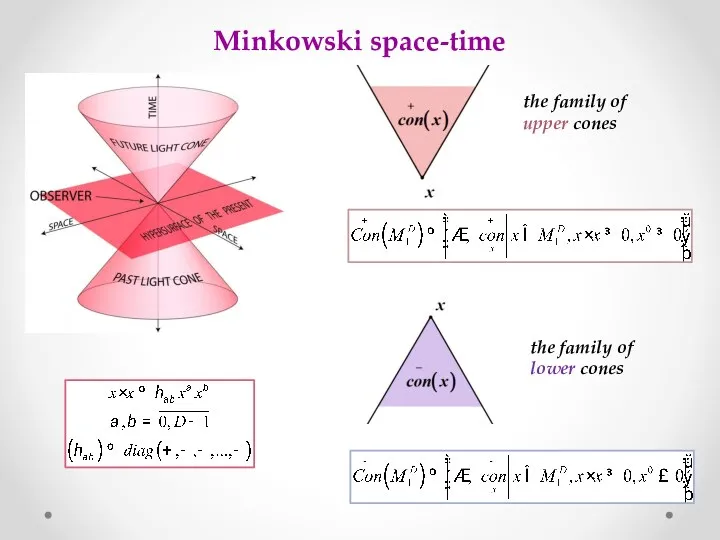
- 9. Minkowski space-time the family of upper cones the family of lower cones
- 10. Operations on upper cones addition multiplication x y z x y z
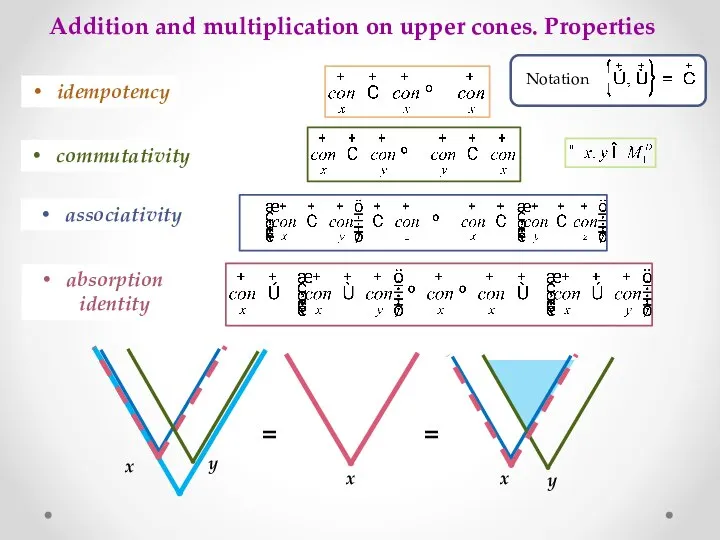
- 11. Addition and multiplication on upper cones. Properties idempotency commutativity associativity absorption identity x y x y
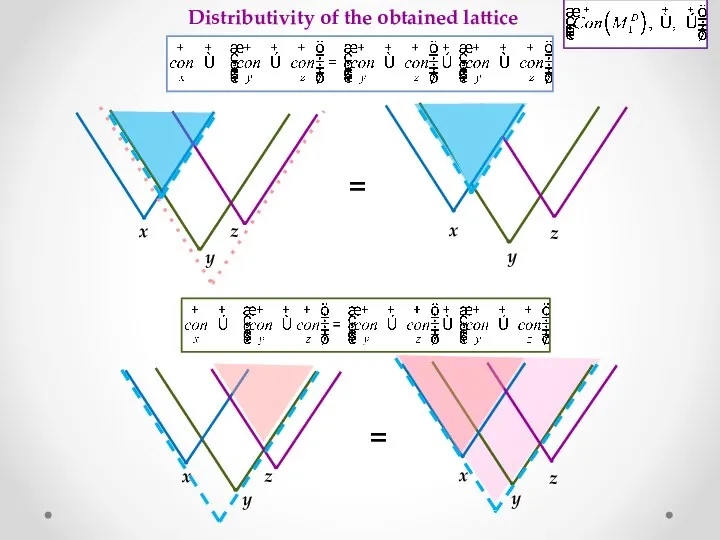
- 12. Distributivity of the obtained lattice = x y z x y z = x y z
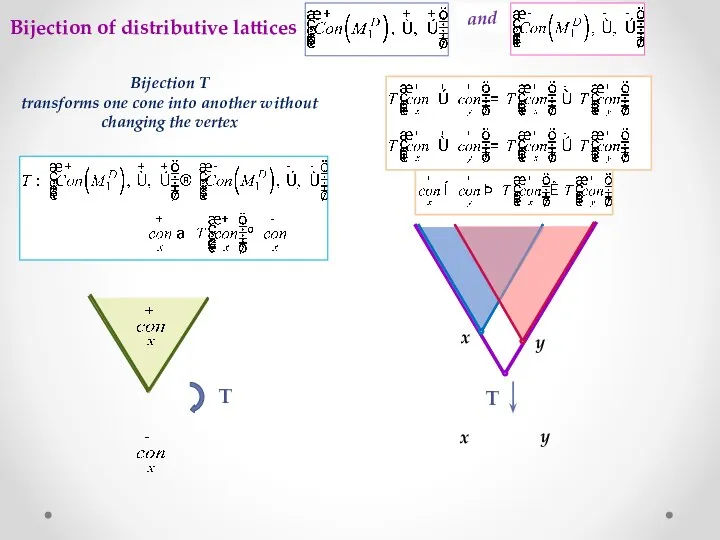
- 13. Bijection of distributive lattices and Bijection T transforms one cone into another without changing the vertex
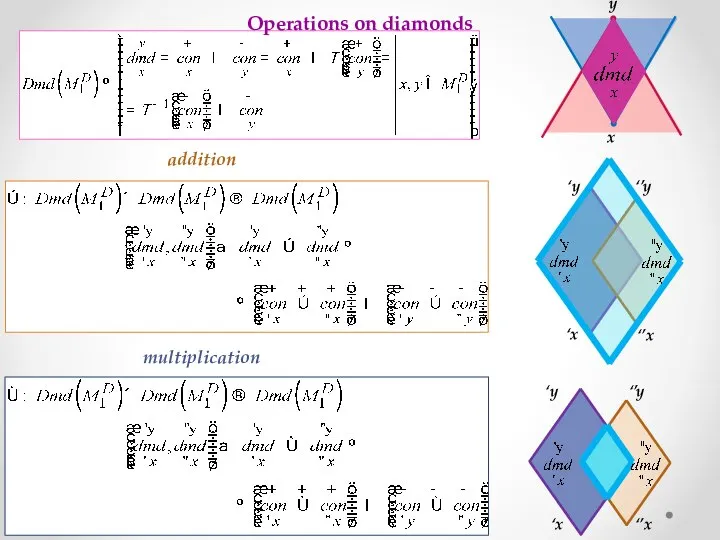
- 14. Operations on diamonds x y addition multiplication ‘x ‘’x ‘y ‘’y ‘x ‘’x ‘y ‘’y
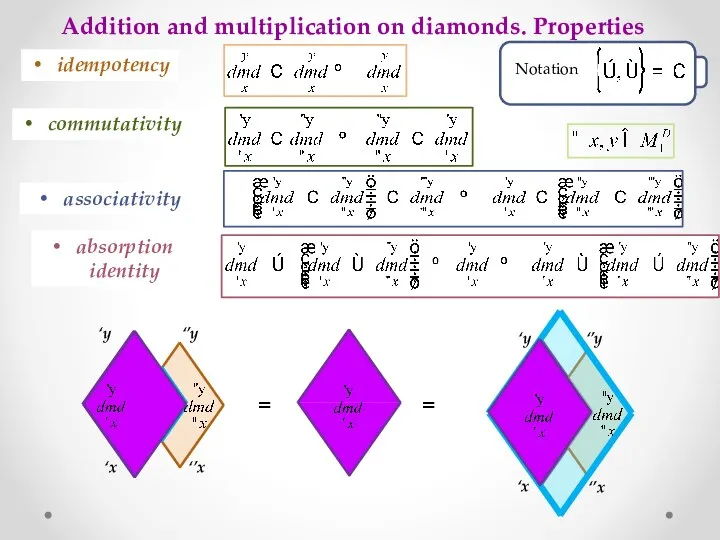
- 15. Addition and multiplication on diamonds. Properties idempotency commutativity associativity absorption identity ‘x ‘’x ‘y ‘’y ‘x
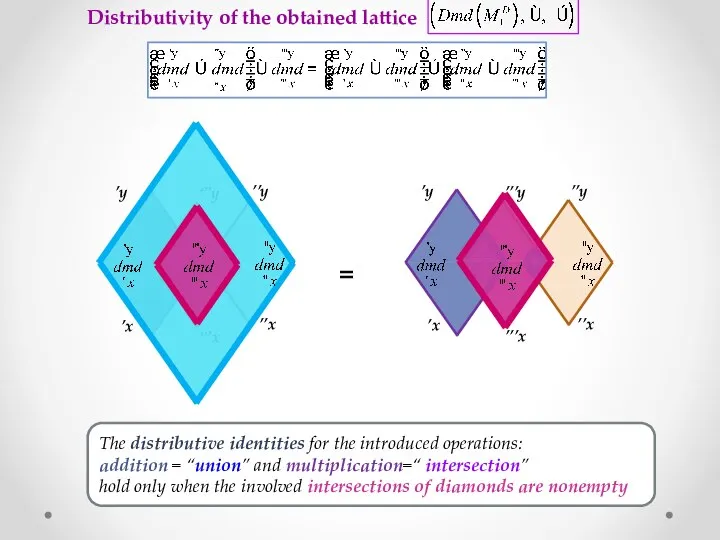
- 16. Distributivity of the obtained lattice ’x ‘’’x ’y ‘’’y ’’x ’’y ’x ’’’x ’y ’’’y ’’x
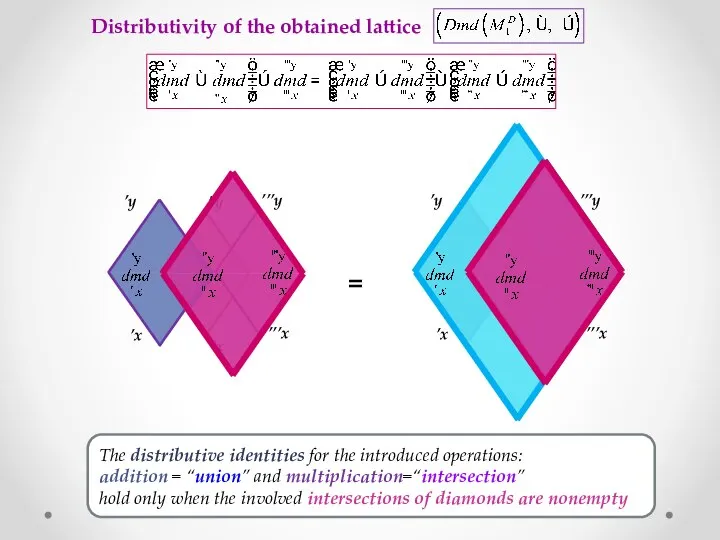
- 17. Distributivity of the obtained lattice ’x ’’x ’y ’’y ’’’x ’’’y ’x ’’x ’y ’’y ’’’x
- 19. Скачать презентацию




 Сфера. Окружность и круг
Сфера. Окружность и круг Решение логических задач. 7 класс
Решение логических задач. 7 класс 1_урок_Повторение_Четырехугольники_Площадь
1_урок_Повторение_Четырехугольники_Площадь Уравнения. Итоговый урок, 7 класс
Уравнения. Итоговый урок, 7 класс Вычисление логарифмов по свойствам
Вычисление логарифмов по свойствам Иррациональные уравнения
Иррациональные уравнения Логарифмов В нашей жизни
Логарифмов В нашей жизни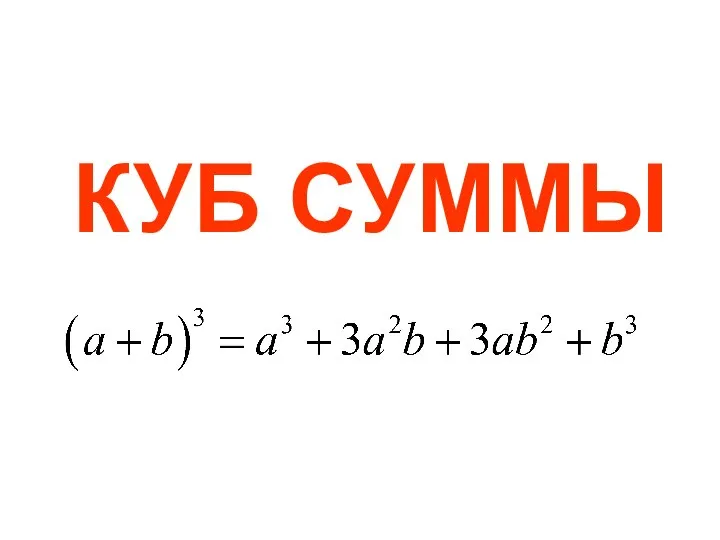 Куб суммы
Куб суммы Ладога в цифрах
Ладога в цифрах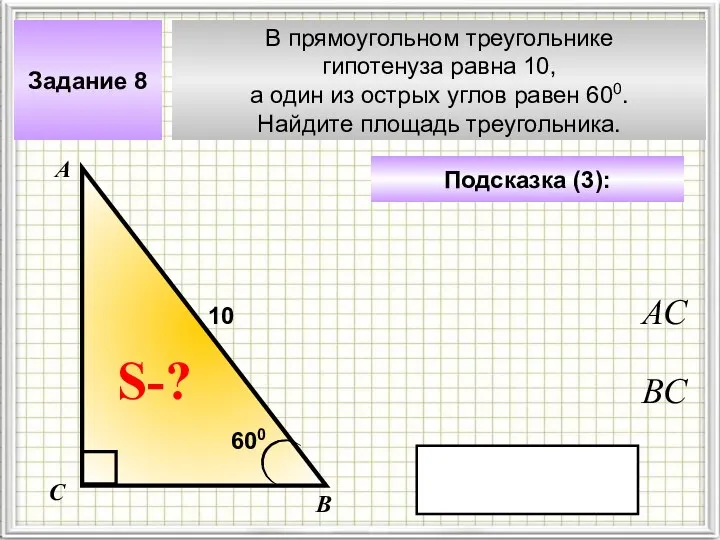 Треугольники (задачи для 9 класса)
Треугольники (задачи для 9 класса) Координатная плоскость. Задания для интерактивной доски
Координатная плоскость. Задания для интерактивной доски По следам теоремы Пифагора
По следам теоремы Пифагора Закрепление изученного. Решение задач
Закрепление изученного. Решение задач Уравнения
Уравнения Презентация на тему Призма и ее свойства
Презентация на тему Призма и ее свойства  Применение аксиом и их следствий
Применение аксиом и их следствий Рационал бөлшектер
Рационал бөлшектер Логические законы
Логические законы Сложение вида +2, +3
Сложение вида +2, +3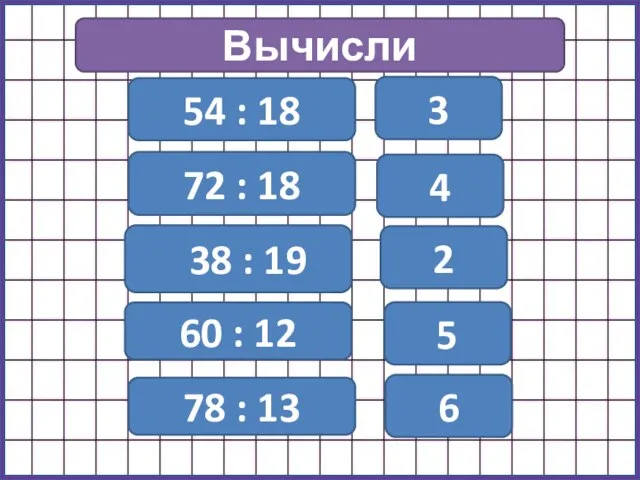 Построение симметричных фигур
Построение симметричных фигур Рекуррентные соотношения
Рекуррентные соотношения Конкурс капитанов
Конкурс капитанов Тригонометрические функции, их свойства и графики
Тригонометрические функции, их свойства и графики Архитектура и параллелепипед
Архитектура и параллелепипед Викторина О, счастливчик (шуточные тесты математика вокруг нас)
Викторина О, счастливчик (шуточные тесты математика вокруг нас) Психогеометрия
Психогеометрия Приём вычислений вида 35 - 7. 2 класс
Приём вычислений вида 35 - 7. 2 класс Что такое угол
Что такое угол