Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов
Содержание
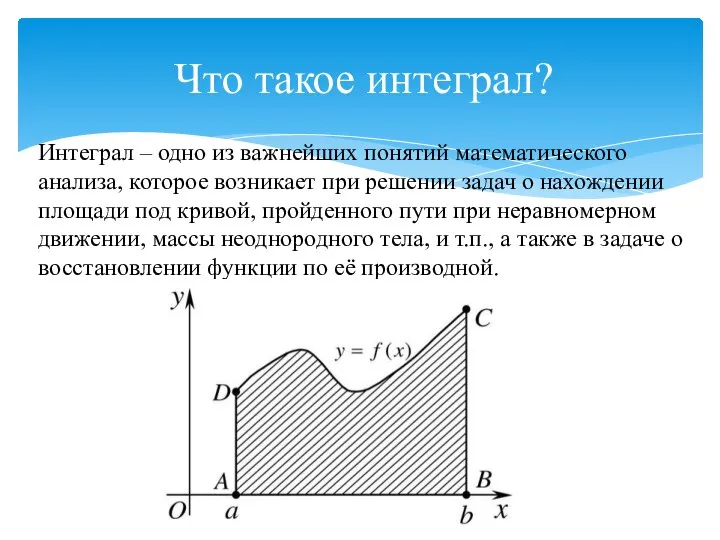
- 2. Что такое интеграл? Интеграл – одно из важнейших понятий математического анализа, которое возникает при решении задач
- 3. Определенный интеграл Определенный интеграл от функции f (x) , непрерывной на отрезке [a,b], вычисляется по формуле:
- 4. 1. Значение определенного интеграла не зависит от обозначения переменной интегрирования: 2. Постоянный множитель можно выносить за
- 5. 4. Если функция y=f(x) интегрируема на [a,b] и a 5. (теорема о среднем). Если функция y=f(x)
- 6. Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – какая-либо ее первообразная на этом отрезке,
- 7. Пример 1. вычислить интеграл Решение. Для подынтегральной функции f(x)=x2 произвольная первообразная имеет вид Так как в
- 8. Вычисление длин дуг с помощью определенного интеграла. Если x=x(t), y=y(t), t∈[t1,t2] – параметрические уравнения гладкой кривой,
- 9. Пример. Вычислить Область интегрирования – часть смещенного круга, ограниченная кривыми
- 10. Вычисление площади с помощью интеграла Криволинейная трапеция – фигура, ограниченная отрезком [a,b] оси Ох, отрезками прямых
- 11. Вычисление объема с помощью определенного интеграла Если тело заключено между двумя перпендикулярными к оси Ox плоскостями,
- 13. Скачать презентацию


![4. Если функция y=f(x) интегрируема на [a,b] и a 5. (теорема о](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/989965/slide-4.jpg)
![Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – какая-либо ее](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/989965/slide-5.jpg)

![Вычисление длин дуг с помощью определенного интеграла. Если x=x(t), y=y(t), t∈[t1,t2] –](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/989965/slide-7.jpg)

![Вычисление площади с помощью интеграла Криволинейная трапеция – фигура, ограниченная отрезком [a,b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/989965/slide-9.jpg)

 Информационная безопасность. Базовые логические элементы, применяемые в вычислительной технике
Информационная безопасность. Базовые логические элементы, применяемые в вычислительной технике Методы решения задач на смеси и сплавы
Методы решения задач на смеси и сплавы Задача о трех игральных костях. Элементарный способ
Задача о трех игральных костях. Элементарный способ Алгоритмы решения простейших тригонометрических неравенств
Алгоритмы решения простейших тригонометрических неравенств Евклидовы пространства
Евклидовы пространства Задача. 1 класс
Задача. 1 класс Скрещивающиеся прямые
Скрещивающиеся прямые Математические ребусы
Математические ребусы Путешествие по реке Математическая. Игра
Путешествие по реке Математическая. Игра Квадратные уравнения
Квадратные уравнения Теорема Байеса
Теорема Байеса Площадь поверхности
Площадь поверхности Презентация на тему Применение производной
Презентация на тему Применение производной  Первое знакомство с понятием вероятность. Самостоятельная работа. 6 класс
Первое знакомство с понятием вероятность. Самостоятельная работа. 6 класс Вычитание чисел 6,7,8,9
Вычитание чисел 6,7,8,9 Конус. Поверхность конуса
Конус. Поверхность конуса Перпендикуляр и наклонная. Теорема о трёх перпендикулярах
Перпендикуляр и наклонная. Теорема о трёх перпендикулярах Метр. (2класс)
Метр. (2класс) Использование современных программных комплексов в расчете строительных конструкций. Получение матриц элементов
Использование современных программных комплексов в расчете строительных конструкций. Получение матриц элементов Аналитическая запись функций алгебры логики
Аналитическая запись функций алгебры логики Пирамида. Усеченная пирамида
Пирамида. Усеченная пирамида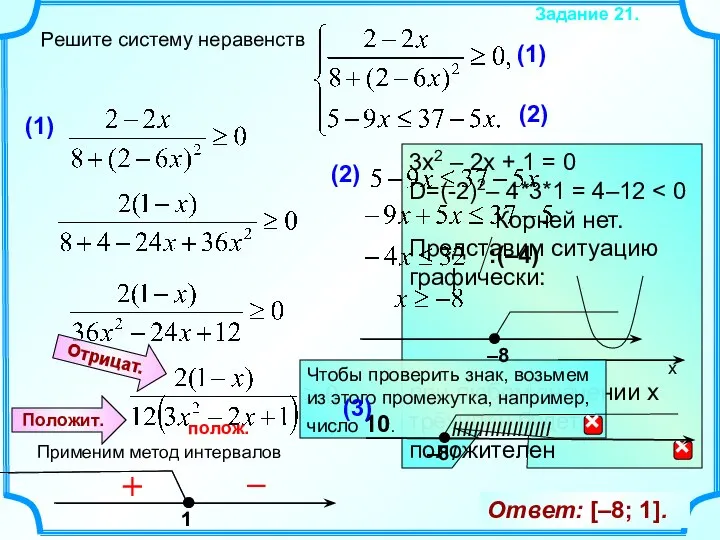 Системы неравенств
Системы неравенств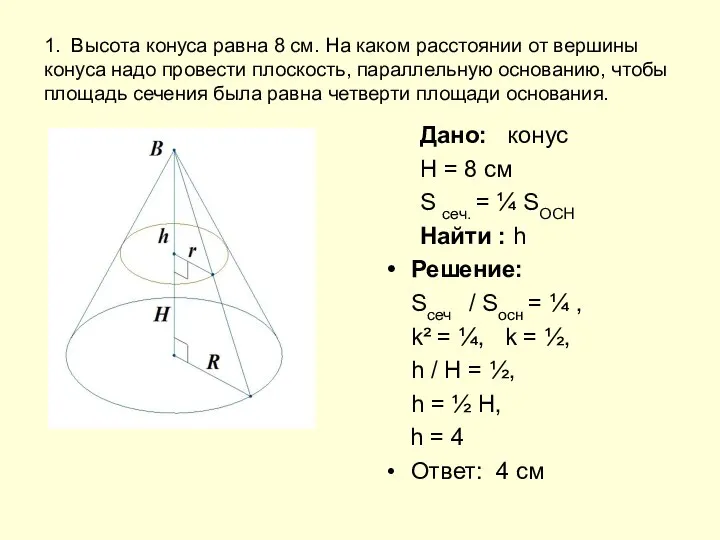 Объём конуса
Объём конуса Презентация на тему Геометрические построения в школьном курсе математики
Презентация на тему Геометрические построения в школьном курсе математики  Показательная функция. Её свойства
Показательная функция. Её свойства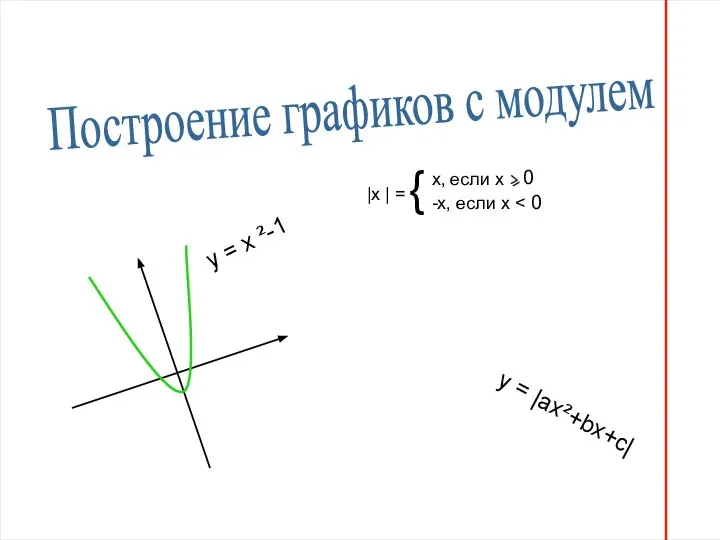 Построение графиков с модулем
Построение графиков с модулем Задания по уровням. Проверь себя
Задания по уровням. Проверь себя Таблица умножения девяти. Тренажёр-раскраска
Таблица умножения девяти. Тренажёр-раскраска