Слайд 2Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны
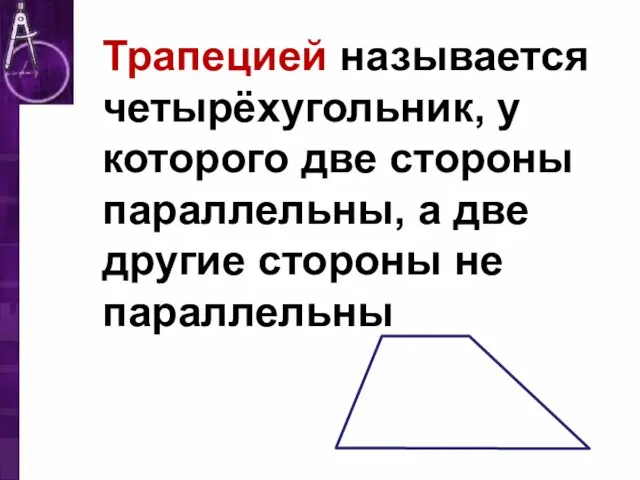
не параллельны
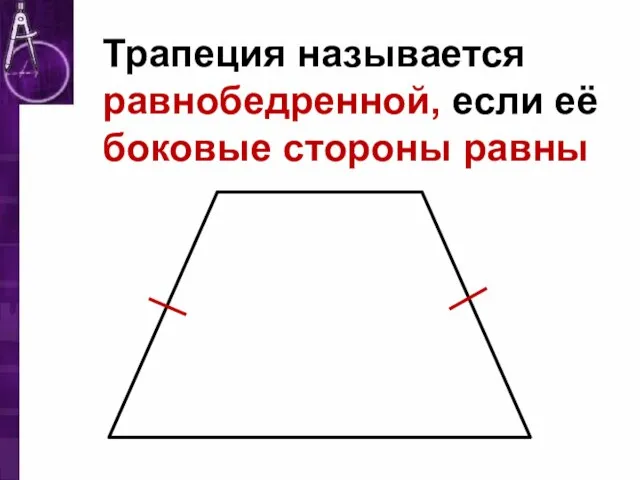
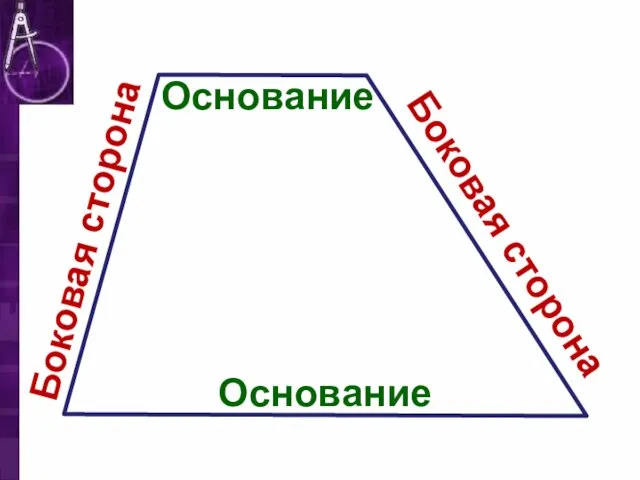
Слайд 4Трапеция называется равнобедренной, если её боковые стороны равны
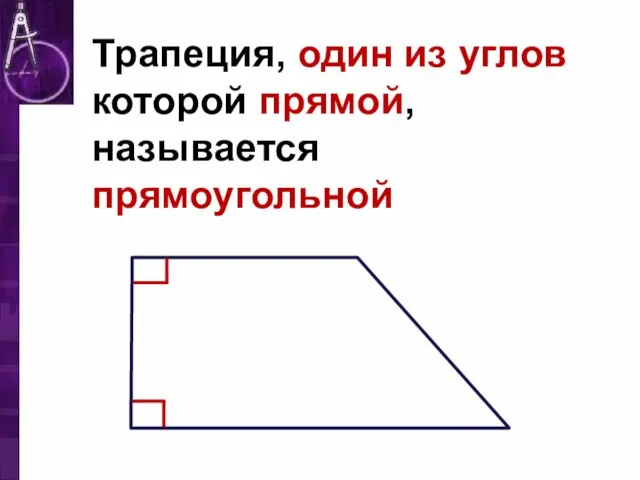
Слайд 5Трапеция, один из углов которой прямой, называется прямоугольной
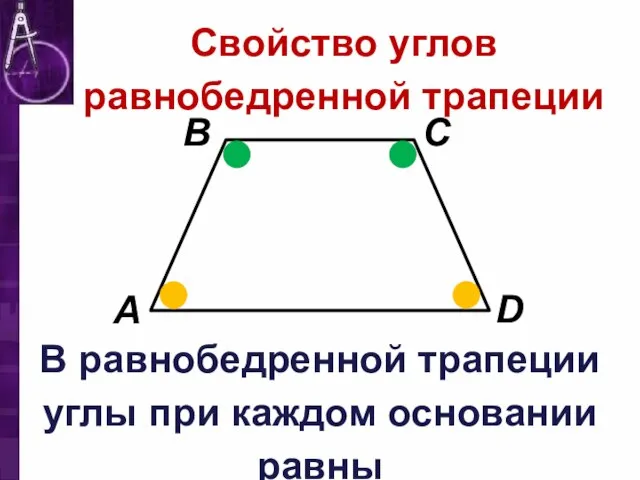
Слайд 6Свойство углов равнобедренной трапеции
В равнобедренной трапеции углы при каждом основании равны
Слайд 7Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции
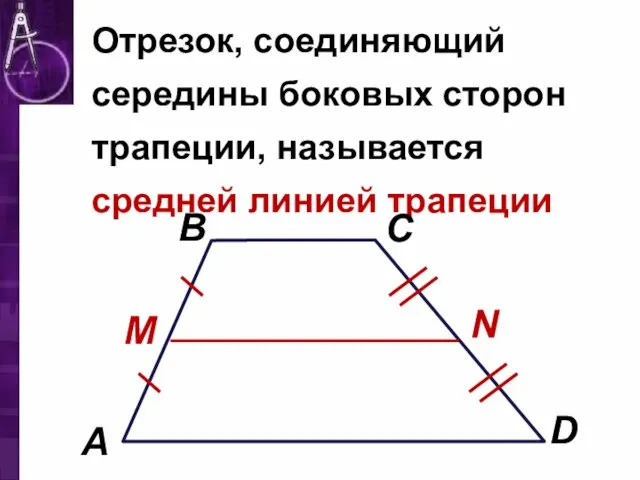
Слайд 8M – середина АВ,
N – середина CD
MN – средняя линия трапеции
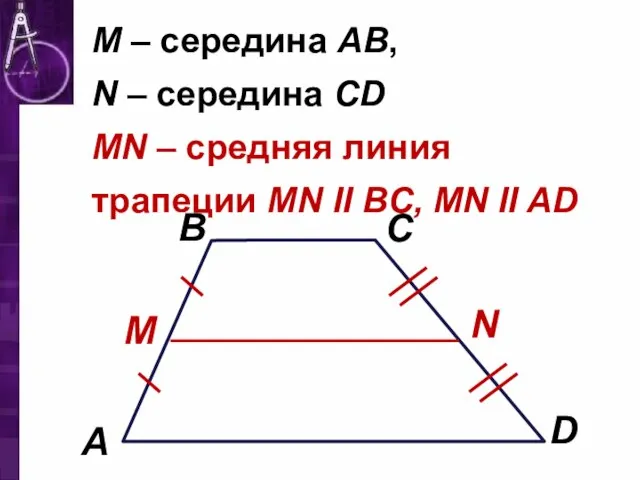
MN II BC, MN II AD
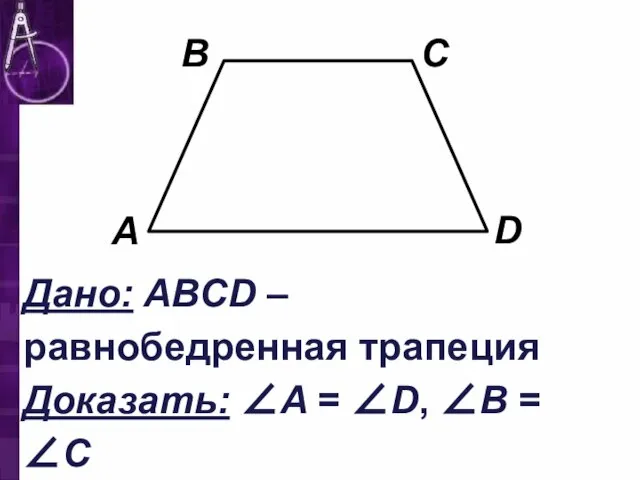
Слайд 9Дано: ABCD – равнобедренная трапеция Доказать: ∠A = ∠D, ∠B = ∠C
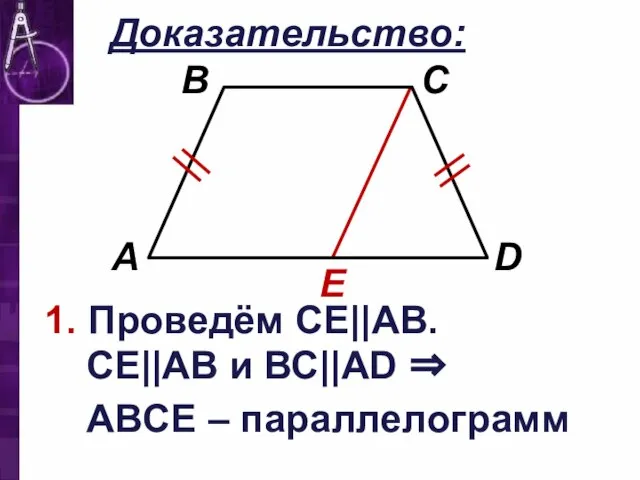
Слайд 10Доказательство:
E
1. Проведём СЕ||АВ.
СЕ||АВ и ВС||АD ⇒
ABCЕ – параллелограмм
Слайд 11Доказательство:
E
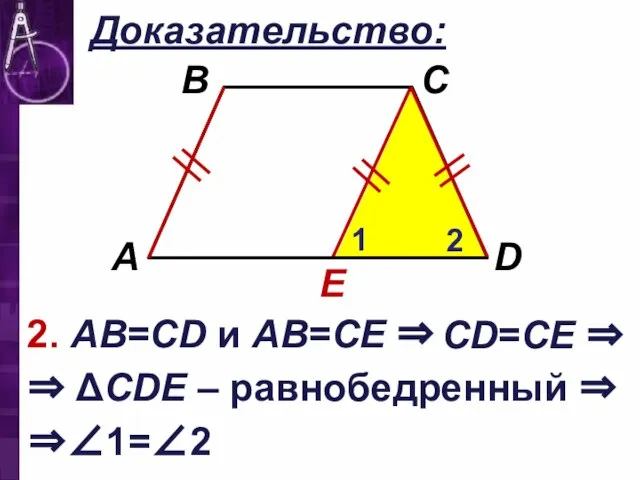
2. АВ=CD и АВ=СЕ ⇒
1
2
⇒ ΔCDЕ – равнобедренный ⇒
CD=СЕ ⇒
⇒∠1=∠2
Слайд 12Доказательство:
E
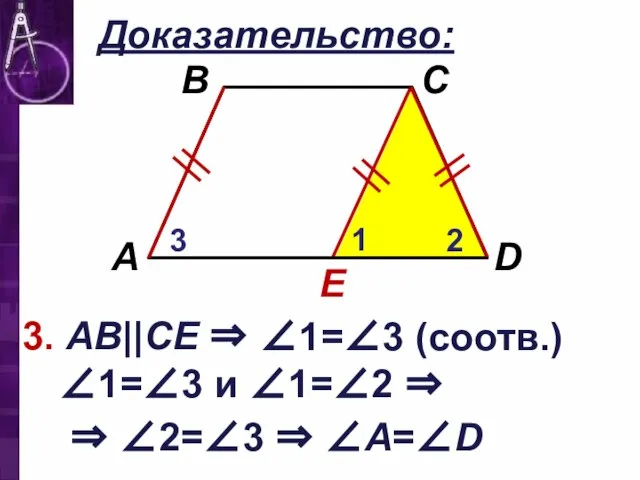
3. АВ||CЕ ⇒
1
2
3
∠1=∠3 (соотв.)
∠1=∠3 и ∠1=∠2 ⇒
⇒ ∠2=∠3 ⇒ ∠А=∠D
Слайд 13Доказательство:
E
4. ∠АВC = 1800 – ∠А
1
2
3
∠ВCD = 1800 – ∠D
∠А=∠D
∠АВC =
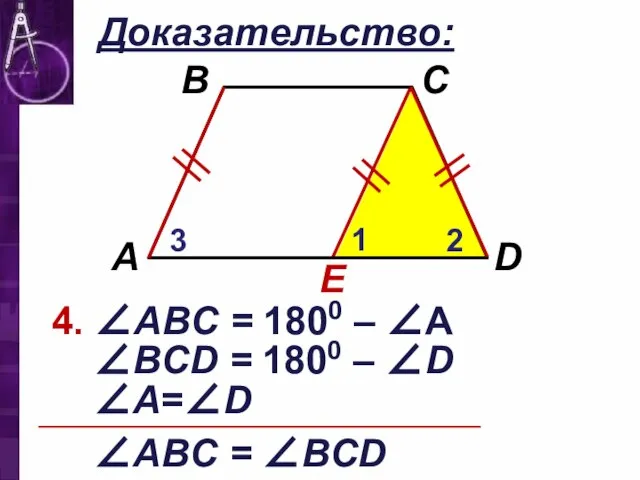
∠ВCD
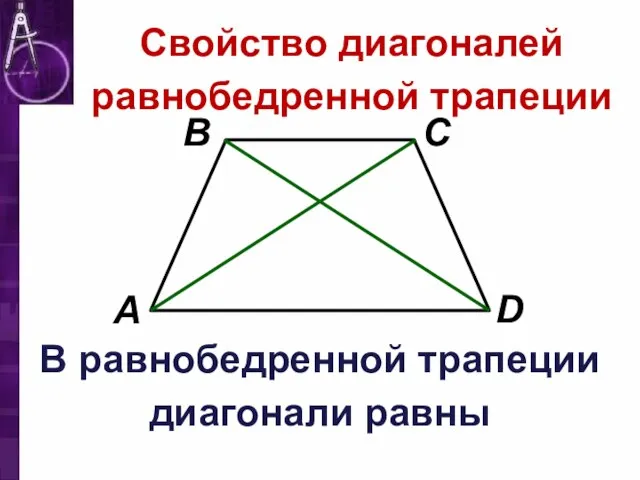
Слайд 14Свойство диагоналей равнобедренной трапеции
В равнобедренной трапеции диагонали равны
Слайд 15Дано: ABCD – равнобедренная трапеция Доказать: АС = ВD
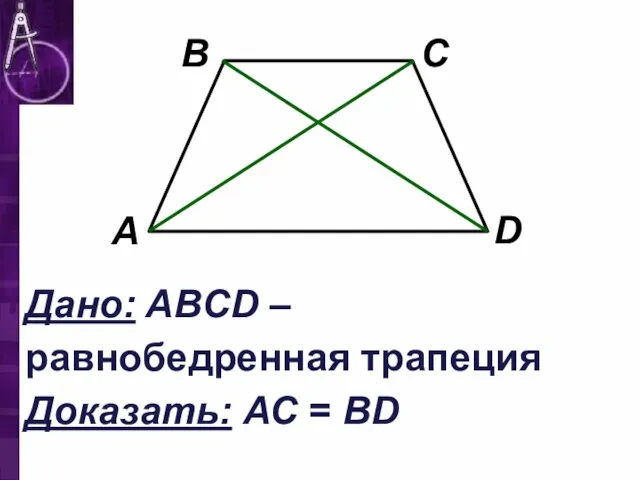
Слайд 16Доказательство:
1. Рассм. ΔАВС и ΔВCD
АB=CD – по опр. равноб. трап.
∠АВС =∠BCD
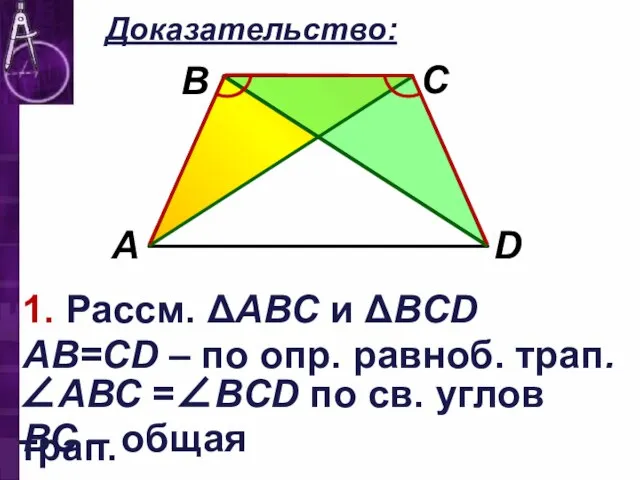
по св. углов трап.
ВС – общая
Слайд 17Доказательство:
2. ΔАВС = ΔВCD по 2 сторонам и углу между ними ⇒
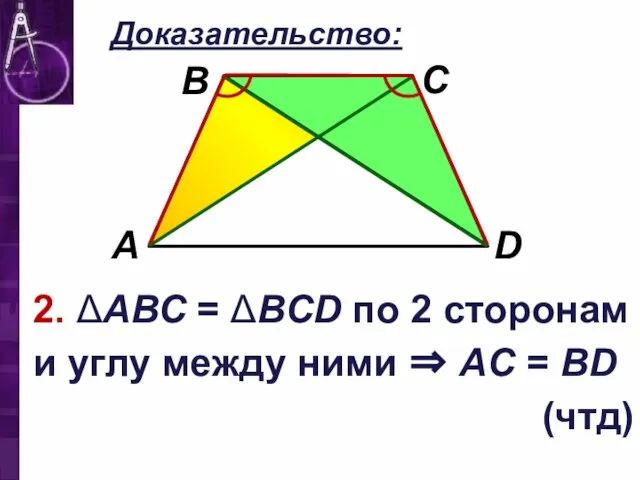
АC = BD
(чтд)
Слайд 18Свойства равнобедренной трапеции
В равнобедренной трапеции углы при каждом основании равны
В равнобедренной трапеции

диагонали равны
Слайд 19Признаки равнобедренной трапеции
Если углы при каждом основании трапеции равны, то она равнобедренная
Если

диагонали трапеции равны, то она равнобедренная
Слайд 20Задача 1
Найдите углы М и Р трапеции MNPQ с основаниями MQ и

NP, если ∠N = 1090, а ∠Q = 370


















 Факториал. Теорема
Факториал. Теорема Способ вычисления двойных интегралов путем сведения их к повторному интегралу
Способ вычисления двойных интегралов путем сведения их к повторному интегралу радианная мера углов
радианная мера углов Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Площади многогранников
Площади многогранников Определение неизвестного числа
Определение неизвестного числа Эйлеровы и гамильтоновы графы
Эйлеровы и гамильтоновы графы ЕГЭ Профиль. Решение задания №7
ЕГЭ Профиль. Решение задания №7 Математика с котом Леопольдом
Математика с котом Леопольдом Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток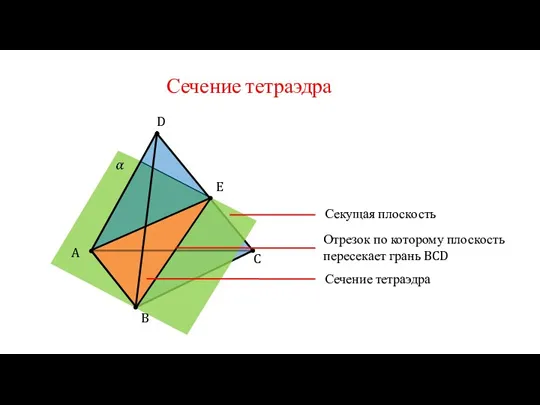 Сечение тетраэдра
Сечение тетраэдра Презентация на тему Умножение и деление натуральных чисел
Презентация на тему Умножение и деление натуральных чисел  Ромб. Свойства параллелограмма
Ромб. Свойства параллелограмма Совокупность математических методов для изучения свойств кубика Рубика
Совокупность математических методов для изучения свойств кубика Рубика Логарифмические уравнения
Логарифмические уравнения Решение задач ЕГЭ
Решение задач ЕГЭ Круги Эйлера в решении задач
Круги Эйлера в решении задач Алгоритм сложения и вычитания двузначных чисел 32 + 45, 77 – 32
Алгоритм сложения и вычитания двузначных чисел 32 + 45, 77 – 32 Методы решения уравнений c модулем
Методы решения уравнений c модулем Элементы теории обобщенных функций
Элементы теории обобщенных функций «Роль игры в процессе обучения на уроках математики»
«Роль игры в процессе обучения на уроках математики» Сантиметр. Линейка
Сантиметр. Линейка Разбиение множеств на классы
Разбиение множеств на классы Математические ребусы
Математические ребусы Уголок математики в подготовительной группе
Уголок математики в подготовительной группе Решение задач. Подготовка к умножению
Решение задач. Подготовка к умножению Начальные геометрические сведения. Параллельные прямые
Начальные геометрические сведения. Параллельные прямые Формулы сокращённого умножения
Формулы сокращённого умножения