Определенный интеграл

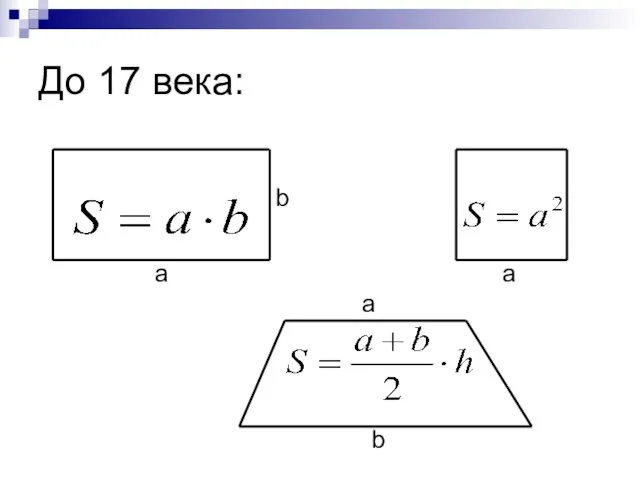
До 17 века:
a
b
a
a
b

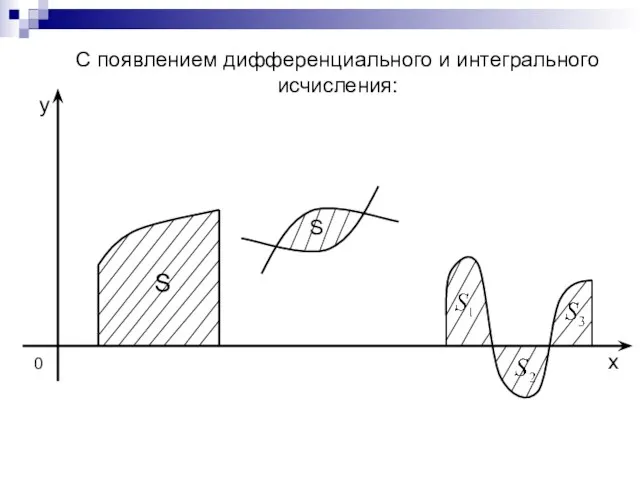
0
x
y
С появлением дифференциального и интегрального исчисления:
S
S

Теорема: Если функция непрерывна на
отрезке [a, b], а функция является первообразной для
на этом отрезке, то справедлива
формула:
(3)
формула Ньютона-Лейбница

И. Ньютон
Г. Лейбниц

Свойства определенного интеграла:
1)
2)
3)
4)
5)

Пример: