Содержание
- 2. Изучение математики в начальной школе направлено на достижение следующих целей:
- 3. 1. математическое развитие младшего школьника — формирование способности к интеллектуальной деятельности (логического и знаково-символического мышления), пространственного
- 4. 2. освоение начальных математиче-ских знаний — понимание значения величин и способов их измерения; использование арифметических способов
- 5. 3. воспитание интереса к математике, стремления использовать математические знания в повседневной жизни.
- 6. Ценностные ориентиры : 1.понимание математических отношений является средством познания закономерностей существования окружающего мира, фактов, процессов и
- 7. 2.математические представления о числах, величинах, геометрических фигурах являются условием целостного восприятия творений природы и человека (памятники
- 8. 3. владение математическим языком, алгоритмами, элементами математической логики позволяет ученику совершенствовать коммуникативную деятельность (аргументировать свою точку
- 9. Личностными результатами обучающихся являются: готовность ученика целенаправленно использовать знания в учении и в повседневной жизни для
- 10. Метапредметными результатами обучающихся являются: способность анализировать учебную ситуацию с точки зрения математических характеристик, устанавливать количественные и
- 11. Метапредметными результатами обучающихся являются: способность анализировать учебную ситуацию с точки зрения математических характеристик, устанавливать количественные и
- 12. Основное содержание обучения в программе представлено крупными разделами: «Числа и величины», «Арифметические действия», «Текстовые задачи», «Пространственные
- 13. Программа по математике позволяет создавать различные модели курса математики, по-разному структурировать содержание учебников, распределять разными способами
- 14. Работа с данными (информацией) Сбор и представление информации, связанной со счётом (пересчётом), измерением величин; фиксирование и
- 15. Составление конечной последовательности (цепочки) предметов, чисел, геометрических фигур и т. п. по правилу. Составление, запись и
- 16. Универсальные учебные действия Личностные Познавательные Регулятивные Коммуникативные
- 17. Личностные универсальные действия личностное, профессиональное, жизненное самоопределение; смыслообразование, т.е. установление обучающимися связи между целью учебной деятельности
- 18. Регулятивные универсальные действия целеполагание как постановка учебной задачи; планирование — определение последовательности промежуточных целей с учётом
- 19. Познавательные универсальные учебные действия 1. Общеучебные самостоятельное выделение и формулирование познавательной цели; поиск и выделение необходимой
- 20. 2. Универсальные логические действия: анализ объектов с целью выделения признаков (существенных, несущественных); синтез; выбор оснований и
- 21. 3. Постановка и решение проблемы формулирование проблемы; самостоятельное создание способов решения проблем творческого и поискового характера.
- 22. Коммуникативные действия планирование учебного сотрудничества с учителем и сверстниками — определение цели, функций участников, способов взаимодействия;
- 23. Условия развития универсальных учебных действий: включение учащихся в активную мотивирующую учебную и внеучебную деятельность; интеграция учебной
- 24. упрощенное понимание сущности и технологии реализации системно-деятельностного подхода; сложившиеся за предыдущие годы устойчивые стереотипы проведения урока,
- 26. Скачать презентацию























 Логарифмы и их свойства
Логарифмы и их свойства Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Решение простейших логарифмических уравнений
Решение простейших логарифмических уравнений Решение задач. 3 класс
Решение задач. 3 класс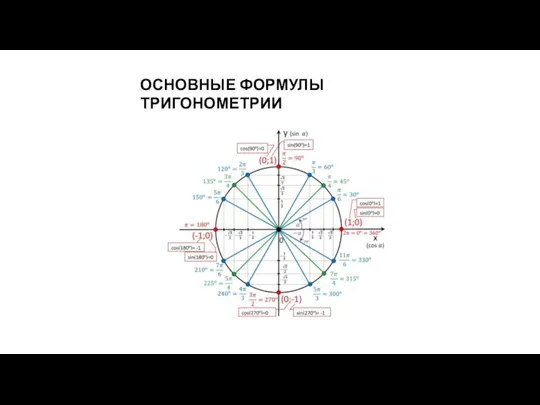 Основные формулы тригонометрии
Основные формулы тригонометрии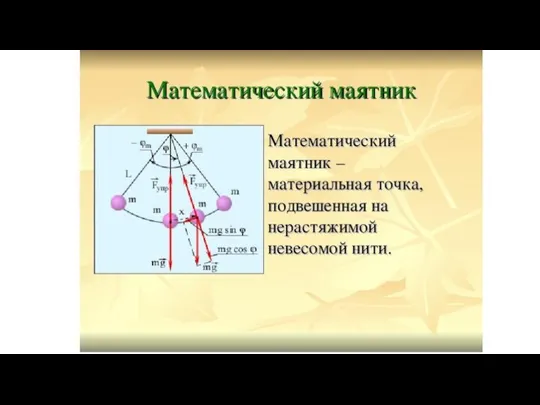 Математический маятник
Математический маятник Окружность и прямая
Окружность и прямая Путешествие по реке Математическая. Игра
Путешествие по реке Математическая. Игра Тренировочный вариант №98
Тренировочный вариант №98 Перпендикуляр и наклонная. 8 класс
Перпендикуляр и наклонная. 8 класс Многочлены. Обобщающий урок - путешествие
Многочлены. Обобщающий урок - путешествие Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Степень числа с натуральным показателем
Степень числа с натуральным показателем Комбинаторика. Перебор вариантов. Решение задач
Комбинаторика. Перебор вариантов. Решение задач Площади фигур
Площади фигур Комплексные числа. Понятие мнимой единицы
Комплексные числа. Понятие мнимой единицы Корреляционный и спектральный анализ случайных процессов
Корреляционный и спектральный анализ случайных процессов Свидетели истории народа
Свидетели истории народа Действия над матрицами. Вычисление определителей второго и третьего порядков
Действия над матрицами. Вычисление определителей второго и третьего порядков Длиннее, короче. Одинаковые по длине
Длиннее, короче. Одинаковые по длине Старинные задачи с использованием дробей
Старинные задачи с использованием дробей Вывод формулы длины окружности и площади круга
Вывод формулы длины окружности и площади круга Дискретная математика
Дискретная математика Алгоритм Джонсона
Алгоритм Джонсона Типовые законы распределения непрерывных случайных величин. Лекция №8_
Типовые законы распределения непрерывных случайных величин. Лекция №8_ Вычисление логарифмов
Вычисление логарифмов Логарифмы и их свойства
Логарифмы и их свойства Міра. Однозначні, багатозначні міри
Міра. Однозначні, багатозначні міри