Содержание
- 2. Определителем первого порядка называется число, Определителем первого порядка называется число, которое определяется по правилу
- 3. Определителем второго порядка называется число, Определителем второго порядка называется число, которое определяется по правилу Пример.
- 4. Определителем третьего порядка называется число, Определителем третьего порядка называется число, которое определяется по правилу
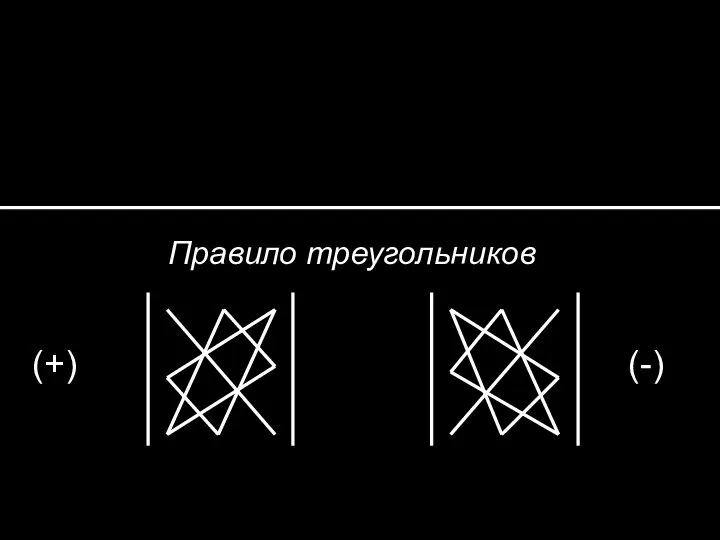
- 5. Правило треугольников (+) (-)
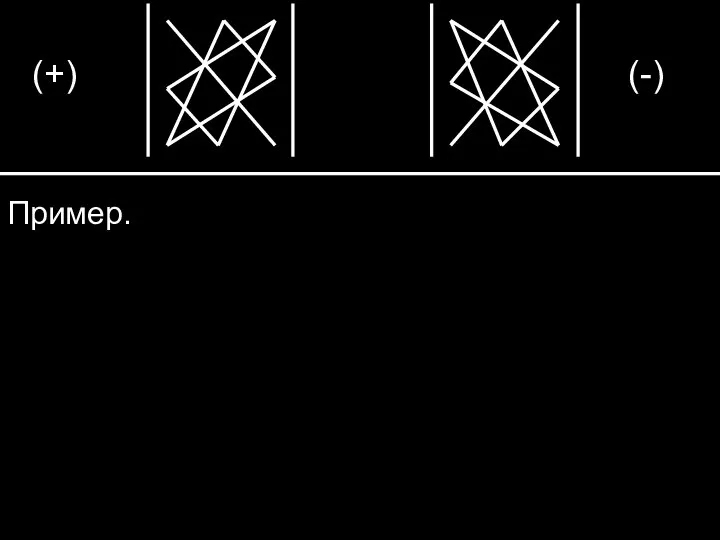
- 6. (+) (-) Пример.
- 7. (+) (-) Пример.
- 8. Свойства определителей 1. Если определитель транспонировать, то его значение не изменится. Пример. Проверить самостоятельно.
- 9. 2. Если в определителе поменять местами любые две строки или столбца, то он изменит знак. Пример.
- 10. 3. Если любую строку (столбец) определителя умножить на число, то получим определитель равный исходному, умноженному на
- 11. 4. Если все элементы какой-либо строки (столбца) определителя равны нулю, то определитель равен нулю. Пример. Проверить
- 12. 5. Если соответствующие элементы каких-либо двух строк (столбцов) равны между собой, то определитель равен нулю. Пример.
- 13. Замечание 1. Если элементы какой-либо строки (столбца) пропорциональны соответствующим элементам другой строки (столбца), то определитель равен
- 14. 6. Если элементы какой-либо строки (столбца) являются суммой двух слагаемых, то определитель можно разложить на сумму
- 15. 7. Если к элементам какой-либо строки (столбца) определителя 7. Если к элементам какой-либо строки (столбца) определителя
- 16. Пример. Проверить самостоятельно. Первую строку домножим на (-2) и сложим со второй. Первую строку сложим с
- 17. Минором элемента определителя называется определитель, получаемый из исходного вычеркиванием Обозначается: Пример. называется определитель, получаемый из исходного
- 18. Пример. Алгебраическим дополнением элемента определителя называется число, которое обозначается и равное
- 19. Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения. Теорема 1 (Лапласа). Доказательство.
- 20. Пример.
- 21. Выберем ту строку (столбец), которая содержит наибольшее количество нулей.
- 22. Теорема 2 (аннулирования). Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой
- 23. Матрица называется обратной к матрице , Матрица называется обратной к матрице , если выполняются равенства: п.2.
- 24. Нахождение обратной матрицы ─ определитель матрицы A ─ алгебраическое дополнение
- 25. Доказательство. Рассмотрим матрицу Найдем произведение
- 26. Применяем теоремы Лапласа и аннулирования Значит, или Аналогично, По определению
- 27. Пример. матрица A невырождена, существует
- 29. Свойства обратной матрицы 1) 2) 3)
- 30. п.3. Ранг матрицы Рассмотрим матрицу Пусть Выделим в матрице k строк и k столбцов. Из элементов,
- 31. Пример. Составим минор 3-го порядка.
- 32. Рангом матрицы называется Рангом матрицы называется наибольший порядок отличного от нуля минора этой матрицы. Пример. Обозначается
- 33. Свойства ранга матрицы 1) Ранг матрицы не меняется при транспонировании. 2) Ранг матрицы не меняется при
- 35. Скачать презентацию






























 Производная функции, заданной параметрически
Производная функции, заданной параметрически Информационная безопасность. Базовые логические элементы, применяемые в вычислительной технике
Информационная безопасность. Базовые логические элементы, применяемые в вычислительной технике Количественные характеристики встречаемости заболеваний
Количественные характеристики встречаемости заболеваний Описательная статистика
Описательная статистика Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 Деление чисел
Деление чисел Векторы в пространстве
Векторы в пространстве Презентация на тему Нахождение площадей ромба, параллелограмма
Презентация на тему Нахождение площадей ромба, параллелограмма  Презентация на тему Формулы для вычисления площади треугольника
Презентация на тему Формулы для вычисления площади треугольника  Урок повторения и самоконтроля
Урок повторения и самоконтроля Свойства параллельных прямых. Урок 37
Свойства параллельных прямых. Урок 37 Векторное и смешанное произведение векторов
Векторное и смешанное произведение векторов Многогранники. Решение задач
Многогранники. Решение задач Математика. Число 10 (1 класс)
Математика. Число 10 (1 класс) Решение логических задач
Решение логических задач Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями Окружность и круг
Окружность и круг Конкурс Удивительные дети (10 класс)
Конкурс Удивительные дети (10 класс) Комплексные числа. Понятие мнимой единицы. Алгебраическая форма комплексного числа. Последовательности
Комплексные числа. Понятие мнимой единицы. Алгебраическая форма комплексного числа. Последовательности Презентация на тему ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Презентация на тему ЭЛЕМЕНТЫ КОМБИНАТОРИКИ  Образование чисел из одного десятка и нескольких единиц. Урок №90
Образование чисел из одного десятка и нескольких единиц. Урок №90 Признаки равенства треугольников. Тест
Признаки равенства треугольников. Тест Числовой коэффициент
Числовой коэффициент Матрицы и определители. Основные понятия и определения. Понятие матрицы
Матрицы и определители. Основные понятия и определения. Понятие матрицы Золотой треугольник и много интересного
Золотой треугольник и много интересного Способы решения тригонометрических уравнений
Способы решения тригонометрических уравнений Дифференциальные уравнения
Дифференциальные уравнения Математическое моделирование. Линейное программирование
Математическое моделирование. Линейное программирование