Содержание
- 2. О А А1 Две точки А и А1 называются симметричными относительно точки О, если О- середина
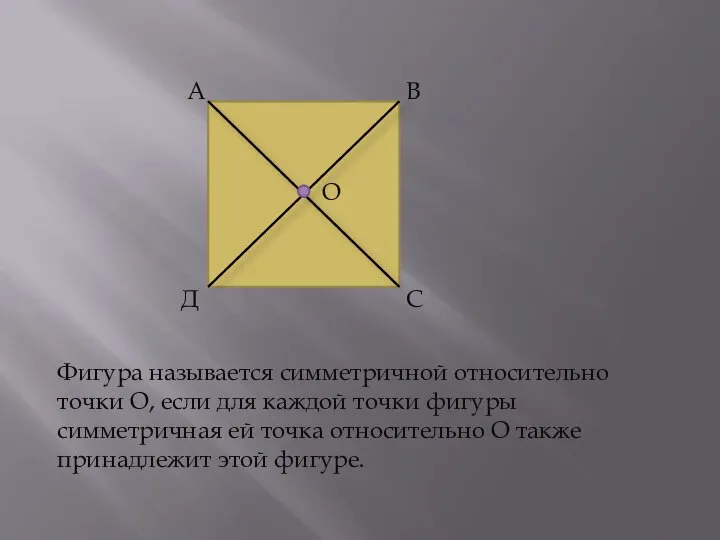
- 3. А В С Д Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная
- 4. Фигуры, обладающие центральной симметрией
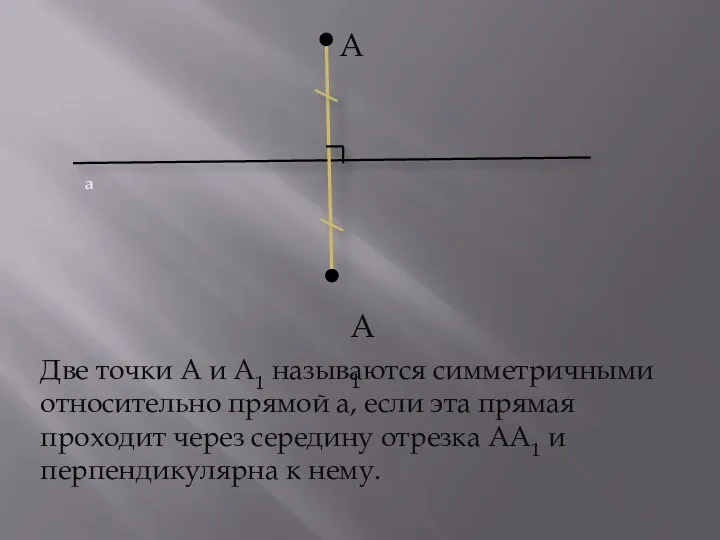
- 5. А Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через
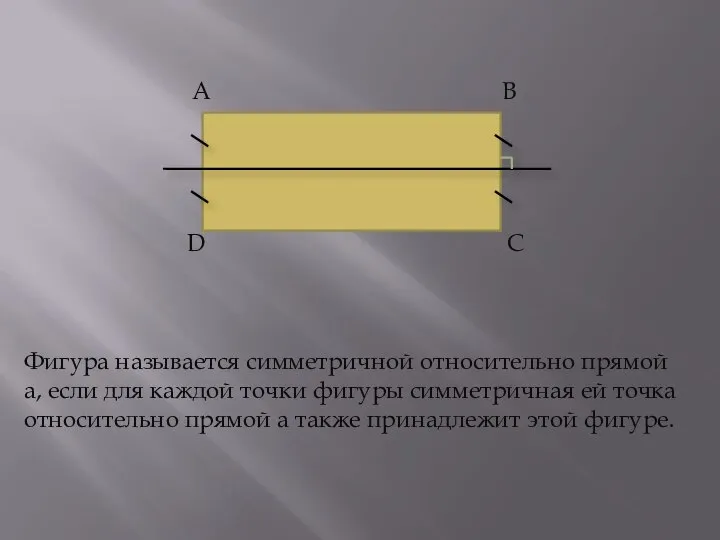
- 6. А В С D Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная
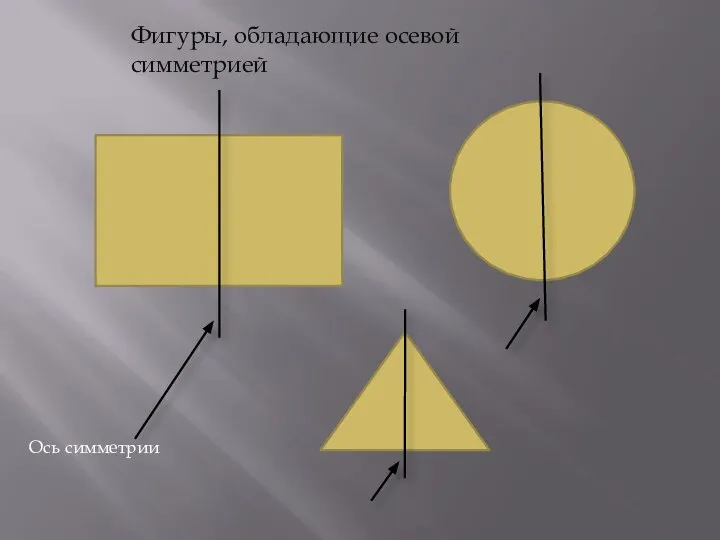
- 7. Ось симметрии Фигуры, обладающие осевой симметрией
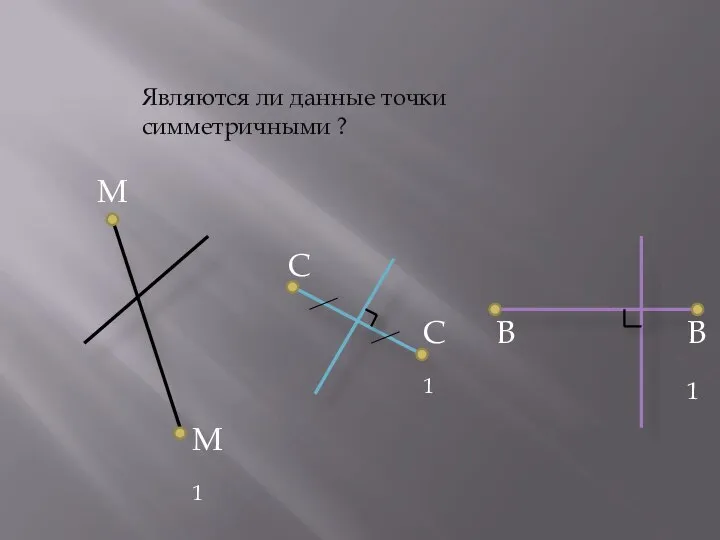
- 8. Являются ли данные точки симметричными ? В В1 М М1 С С1
- 9. Какие из следующих букв имеют ось симметрии: «А Б Г Е О Ф Ж Э» ?
- 10. Проверь себя: 1) точки С иС1 являются симметричными; 2) Буквы А, Е, О, Ф, Ж, Э.
- 11. Симметрия в окружающем мире: в архитектуре, в живой природе, в искусстве.
- 20. Скачать презентацию












 Интегральные уравнения
Интегральные уравнения Как вычислить площадь поверхности тела человека
Как вычислить площадь поверхности тела человека Прямая и плоскость в пространстве. Смешанные задачи
Прямая и плоскость в пространстве. Смешанные задачи Система MatLab. Методические указания к выполнению лабораторных работ
Система MatLab. Методические указания к выполнению лабораторных работ Дискретная математика. Лекция 1. Введение
Дискретная математика. Лекция 1. Введение Презентация на тему Свойства четырехугольников
Презентация на тему Свойства четырехугольников  Пропорция
Пропорция Diskretnaya_matematika_sootvetstvia
Diskretnaya_matematika_sootvetstvia Правильные многоугольники
Правильные многоугольники Построение графика функции
Построение графика функции Правила комбинаторики. Решение комбинаторных задач
Правила комбинаторики. Решение комбинаторных задач Методика обучения решению простых задач
Методика обучения решению простых задач Пифагор. Жизнь и эпоха
Пифагор. Жизнь и эпоха Решение уравнений и неравенств. Задания для самостоятельной работы
Решение уравнений и неравенств. Задания для самостоятельной работы Свойства действий над числами
Свойства действий над числами Системы счисления
Системы счисления Решите систему неравенств и укажите все целые числа, которые являются ее решениями
Решите систему неравенств и укажите все целые числа, которые являются ее решениями Векторы
Векторы Решение уравнений третьей степени
Решение уравнений третьей степени Модуль числа. 6 класс
Модуль числа. 6 класс Признаки параллельности прямых
Признаки параллельности прямых Прямоугольный параллелепипед
Прямоугольный параллелепипед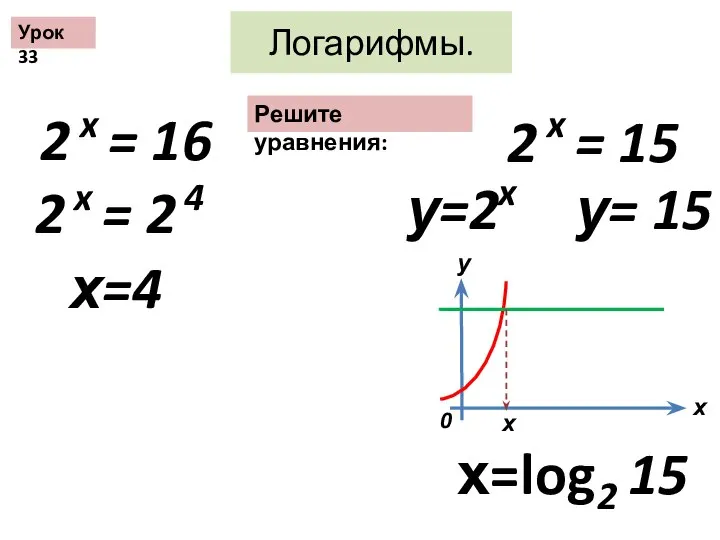 Логарифмы
Логарифмы Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа История развития математики
История развития математики Координаты вектора
Координаты вектора Сантиметр. Линейка
Сантиметр. Линейка Презентация на тему Физико-математический КВН в 9-х классах
Презентация на тему Физико-математический КВН в 9-х классах