Содержание
- 2. Свойства координат векторов: 1. Координаты нулевого вектора в любом из базисов равны нулю. 2. Координаты вектора
- 3. Скалярное и векторное произведение векторов. Скалярным произведением двух векторов называется число, равное произведению их модулей на
- 4. Пример 1. Найти скалярное произведение векторов a и b, если: Решение: Известны длины векторов и угол
- 5. Задачи для самостоятельного решения: Найти скалярное произведение векторов a и b, если: 1) 2) 3) См.
- 7. Скачать презентацию




 Показательные уравнения
Показательные уравнения Свойства биссектрисы угла. Решение задач
Свойства биссектрисы угла. Решение задач Сумматор. Таблица истинности сумматора
Сумматор. Таблица истинности сумматора Презентация на тему Длиннее короче
Презентация на тему Длиннее короче  Простые и составные числа
Простые и составные числа Ориентировка в пространстве
Ориентировка в пространстве Радианная мера угла. Поворот точки вокруг начала координат
Радианная мера угла. Поворот точки вокруг начала координат Единица измерения объёма жидкости-литр
Единица измерения объёма жидкости-литр Возведение трехчлена в квадрат
Возведение трехчлена в квадрат Распределенные системы. Математическое представление распределенной системы
Распределенные системы. Математическое представление распределенной системы Треугольник. Повторение. Задачи на проверку истинности утверждений
Треугольник. Повторение. Задачи на проверку истинности утверждений Необычная раскраска по математике
Необычная раскраска по математике Контрольная работа. Логарифм, логарифмическая функция
Контрольная работа. Логарифм, логарифмическая функция Поворот точки вокруг начала координат
Поворот точки вокруг начала координат Многогранники в архитектуре
Многогранники в архитектуре Распределительное свойства умножения
Распределительное свойства умножения Меры измерения времени
Меры измерения времени Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число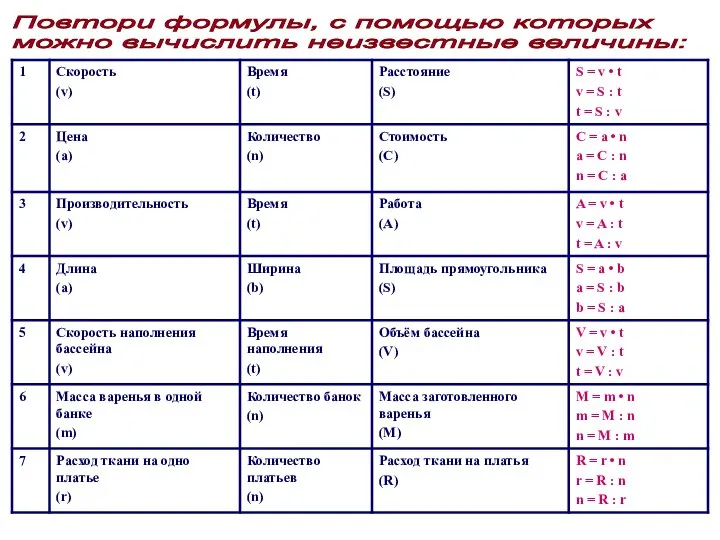 Скорость (v), Время (t), Расстояние (S)
Скорость (v), Время (t), Расстояние (S) Мастер-группа по математике Взлет
Мастер-группа по математике Взлет Занимательные задачи (4 класс)
Занимательные задачи (4 класс) Квадратные уравнения. Урок-путешествие
Квадратные уравнения. Урок-путешествие Естественный отбор. Бинарный урок по биологии и математике (часть 3)
Естественный отбор. Бинарный урок по биологии и математике (часть 3) Путешествие по морям
Путешествие по морям Соседи числа
Соседи числа аксіоми стереометрії
аксіоми стереометрії Открытое акционерное общество в 6 классе
Открытое акционерное общество в 6 классе Решение иррациональных уравнений
Решение иррациональных уравнений