Содержание
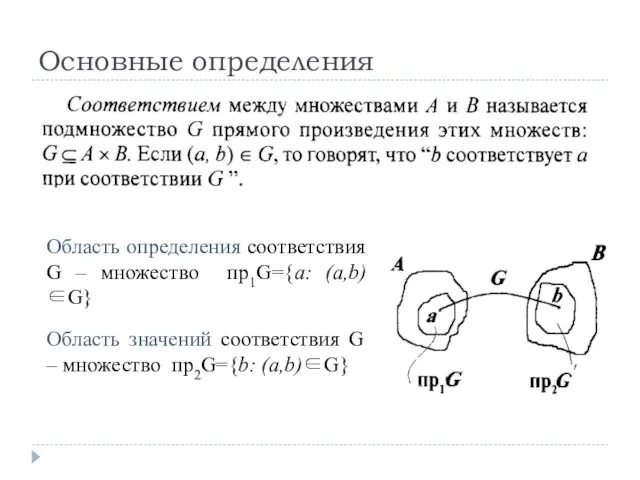
- 2. Основные определения Область определения соответствия G – множество пр1G={a: (a,b)∈G} Область значений соответствия G – множество
- 3. Основные определения Пример 1. Экзаменационная ведомость устанавливает следующее соответствие : А={Иванов, Петров, Сидоров, Конев, Синицын, Васечкин,
- 4. G={(Иванов, 4), (Петров, 2), (Сидоров, 3), (Конев, 4), (Васечкин, 3), (Макарова, 5)}. Область определения соответствия G
- 5. Основные определения В примере 1: образом Иванова является 4; образом Сидорова - 3 и т.д. Прообразом
- 6. Свойства соответствий Соответствие G⊆А×В называется всюду (полностью) определенным, если область определения совпадает с множеством А, т.е.
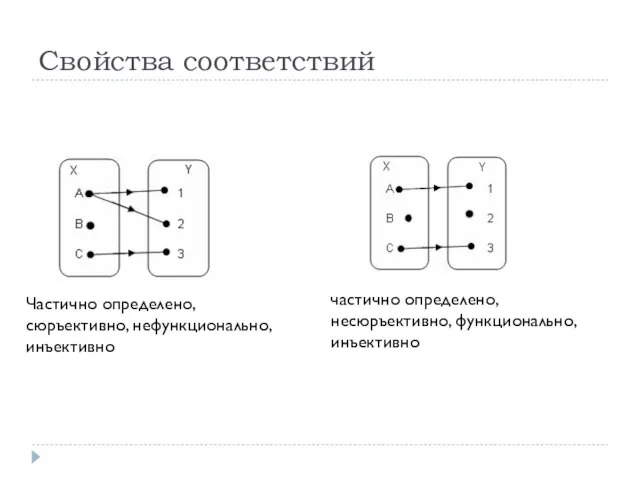
- 7. Свойства соответствий частично определено, несюръективно, функционально, инъективно Частично определено, сюръективно, нефункционально, инъективно
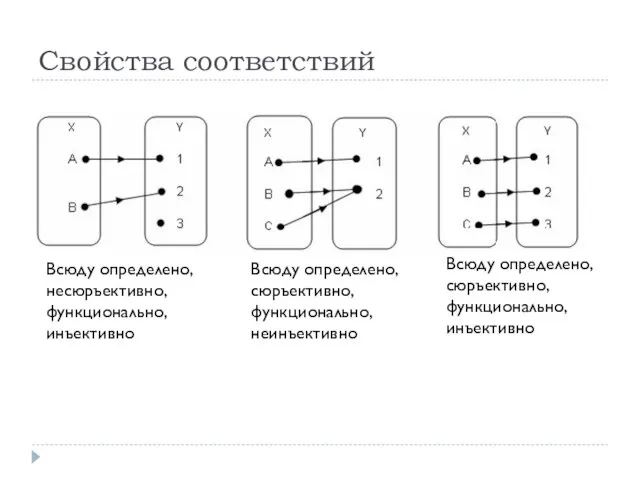
- 8. Свойства соответствий Всюду определено, несюръективно, функционально, инъективно Всюду определено, сюръективно, функционально, неинъективно Всюду определено, сюръективно, функционально,
- 9. Свойства соответствий Определим свойства отношения в примере 1. Частично определено, так как нет образа для Синицына;
- 10. Функции и отображения Функциональное соответствие называется функцией. Если функция f устанавливает соответствие между множествами А и
- 11. Функции и отображения Отображением А в В называется всюду определенная функция f : А→В (обозначается f
- 12. Функции и отображения тип
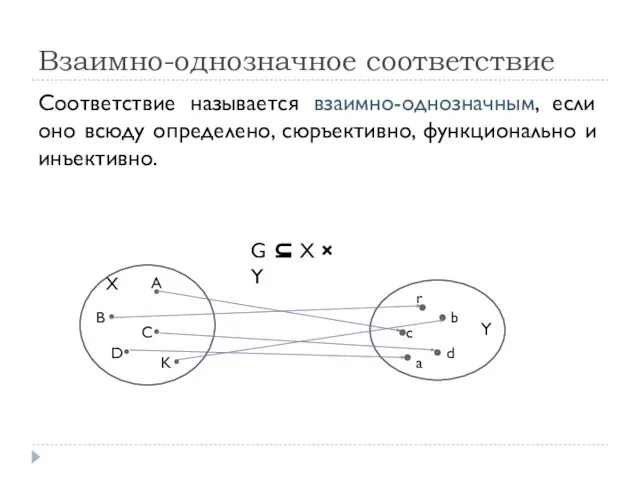
- 13. Взаимно-однозначное соответствие Соответствие называется взаимно-однозначным, если оно всюду определено, сюръективно, функционально и инъективно. A B C
- 14. Мощность множеств Понятие мощности возникает при сравнении множеств по числу элементов. Мощностью конечного множества является число
- 15. Мощность множеств Этот факт позволяет: установить равенство мощностей двух множеств, не вычисляя этих множеств; вычислить мощность
- 16. Счетные множества Любое множество, равномощное множеству всех натуральных чисел, называют счетным. Мощность счетного множества обозначают ℵ0
- 17. Счетные множества Если элемент множества М есть ν(n) для некоторого n∈ N, то этот элемент множества
- 18. Счетные множества Пример. Множество всех нечетных натуральных чисел счетно. Нумерацию ν можно задать так: ν(n) =
- 19. Счетные множества Пример. Множество Z всех целых чисел счетно. Расположим элементы множества целых чисел в определенном
- 20. Счетные множества Нумерацию можно было установить так: Z={…, -5, -4, -3, -2, -1, 0, 1, 2,
- 21. Счетные множества Примеры счетных множеств: Множество рациональных чисел счетно; Множество периодических дробей счетно; Множество всех натуральных
- 22. Счетные множества Докажем, что Множество пар натуральных чисел счетно.
- 23. Счетные множества Теорема. (а) Подмножество счетного множества конечно или счетно. (б) Всякое бесконечное множество содержит счетное
- 24. Несчетные множества Теорема Кантора: Множество всех действительных чисел интервала (0,1) числовой оси несчетно. Всякое множество, эквивалентное
- 26. Скачать презентацию



















 Отношение чисел
Отношение чисел Функциональная грамотность школьников на уроках математики
Функциональная грамотность школьников на уроках математики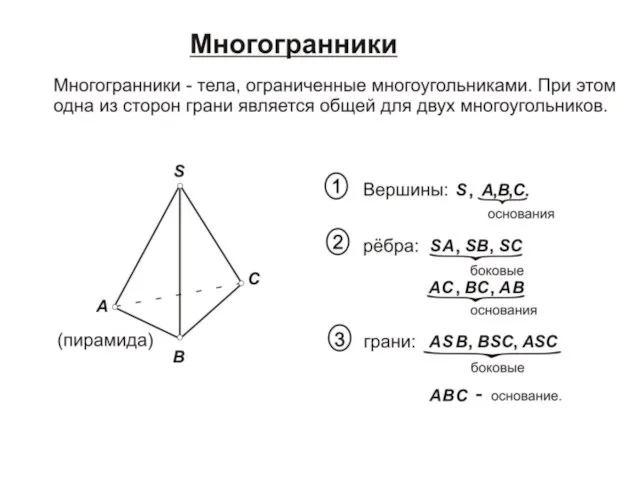 Многогранники + точки. Лекция 5
Многогранники + точки. Лекция 5 Ariile figurilor geometrice plane
Ariile figurilor geometrice plane Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№13)
Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№13)  Градусная мера дуги
Градусная мера дуги Действия над матрицами. Обратная матрица. Лекция 2а
Действия над матрицами. Обратная матрица. Лекция 2а Построение графиков функций с помощью геометрических преобразований
Построение графиков функций с помощью геометрических преобразований Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Проверочная работа. 5 класс
Проверочная работа. 5 класс Логические выражения
Логические выражения Вектор. Равенство векторов. Откладывание вектора равного данному
Вектор. Равенство векторов. Откладывание вектора равного данному Игра Музыкальная математика
Игра Музыкальная математика Умозаключения. Теоремы. Утверждения
Умозаключения. Теоремы. Утверждения Презентация на тему Тетраэдр, виды сечений и решение задач по тетраэдру
Презентация на тему Тетраэдр, виды сечений и решение задач по тетраэдру  Умножение и деление смешанных чисел
Умножение и деление смешанных чисел Плоское зеркало. Построение изображений в плоском зеркале
Плоское зеркало. Построение изображений в плоском зеркале Таблица сложения в пределах 20
Таблица сложения в пределах 20 Задачи на части
Задачи на части Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Симметрия в пространстве
Симметрия в пространстве Площади. Объёмы
Площади. Объёмы Правильные многогранники, полуправильные
Правильные многогранники, полуправильные ВЛИЯНИЕ КОЭФФИЦИЕНТОВ а, b и с НА РАСПОЛОЖЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
ВЛИЯНИЕ КОЭФФИЦИЕНТОВ а, b и с НА РАСПОЛОЖЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ Метрология и теория измерений. Лекция 10
Метрология и теория измерений. Лекция 10 Устный счет
Устный счет Симметрии. Осевая симметрия
Симметрии. Осевая симметрия