Содержание
- 2. Системы уравнений, в которых одно уравнение – алгебраическое, а другое – сумма или разность тригонометрических функций.
- 3. 2. Системы уравнений, в которых одно уравнение – алгебраическое, а другое – произведение тригонометрических функций. Примеры:
- 4. 3. Системы уравнений, в которых одно уравнение – алгебраическое, а другое – отношение тригонометрических функций. Примеры:
- 5. 4. Системы уравнений, содержащих только тригонометрические функции. Примеры:
- 6. 1. Решить систему уравнений Решение. Из (2) следует: Из (1) следует:
- 7. Запишем систему:
- 8. Запишем систему: Если сложить и вычесть уравнения системы, то получим систему, равносильную исходной.
- 9. Ответ:
- 10. 2. Решить систему уравнений Решение. Из (2) следует: Из (1) следует:
- 11. Запишем систему уравнений: Складывая и вычитая уравнения системы, получим систему, равносильную исходной: Ответ:
- 12. 3. Решить систему уравнений Решение. Решим второе уравнение системы: Правую часть уравнения (1) распишем по формуле
- 13. Ответ:
- 14. 4. Решить систему уравнений Решение. Если сложить и вычесть уравнения системы, то получим систему равносильную исходной.
- 15. Применим формулы сложения: При решении независимых простейших уравнений необходимо писать разные целочисленные параметры, иначе будет потеряно
- 17. Скачать презентацию





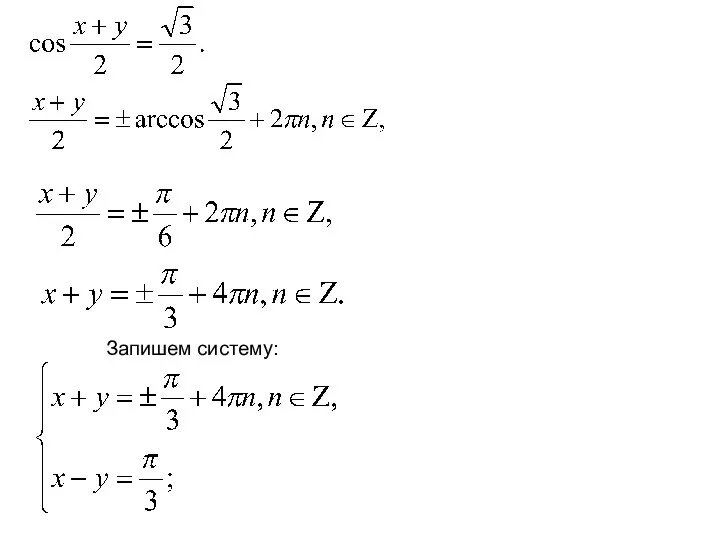

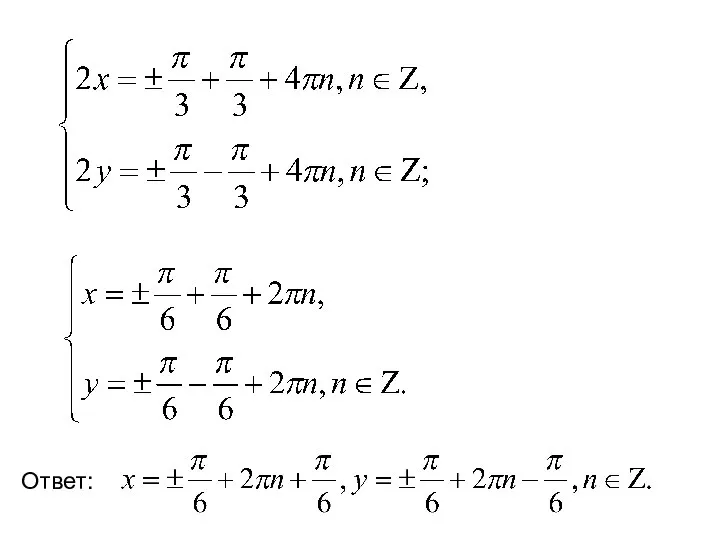



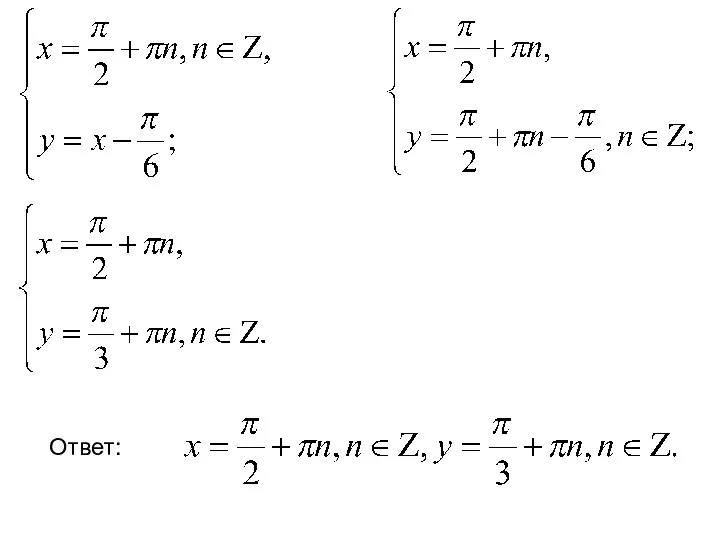


 Тригонометрические уравнения
Тригонометрические уравнения Презентация на тему ГИА-2013г. Модуль АЛГЕБРА №6
Презентация на тему ГИА-2013г. Модуль АЛГЕБРА №6  Первый признак равенства треугольников
Первый признак равенства треугольников Область определения выражения
Область определения выражения Математика в парикмахерском искусстве
Математика в парикмахерском искусстве Этот вездесущий треугольник
Этот вездесущий треугольник Множества и отношения
Множества и отношения Решение систем с неизвестными множествами
Решение систем с неизвестными множествами Тригонометрические функции
Тригонометрические функции Аналитические методы исследования дробнорациональных функций и построение их графиков с использованием программных средств
Аналитические методы исследования дробнорациональных функций и построение их графиков с использованием программных средств Прибавление и вычитание числа 6
Прибавление и вычитание числа 6 Решение неравенств с одной переменной
Решение неравенств с одной переменной Презентация на тему Тригонометрия
Презентация на тему Тригонометрия  Линейные пространства и линейные операторы. Лекция 4
Линейные пространства и линейные операторы. Лекция 4 Применение производной. Демонстрационный материал
Применение производной. Демонстрационный материал Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Производная и дифференцируемость функции
Производная и дифференцируемость функции Презентация на тему Решение уравнения sin t = a
Презентация на тему Решение уравнения sin t = a  Занимательная математика
Занимательная математика Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Презентация на тему Формулы сокращенного умножения (Сумма и разность кубов)
Презентация на тему Формулы сокращенного умножения (Сумма и разность кубов)  Это полезно знать. Интересные факты из жизни самых больших чисел
Это полезно знать. Интересные факты из жизни самых больших чисел Презентация на тему Пропорциональность величин (6 класс)
Презентация на тему Пропорциональность величин (6 класс)  Выберите чётные числа (триггеры)
Выберите чётные числа (триггеры) Понятие многогранника. Призма
Понятие многогранника. Призма Решение задач на применение признаков подобия треугольников
Решение задач на применение признаков подобия треугольников Задачи по аналитической геометрии на плоскости. Уравнения прямой на плоскости
Задачи по аналитической геометрии на плоскости. Уравнения прямой на плоскости Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений