Слайд 2ВЫЧИСЛЕНИЕ ПОСТРОЧНЫХ СРЕДНИХ И
ДИСПЕРСИЙ
.
где (n – 1) – число степеней

свободы, равное количеству
опытов минус единица.
Слайд 3ИСКЛЮЧЕНИЕ ГРУБЫХ ОШИБОК
Наличие резко отклоняющихся результатов (так назы-ваемых "грубых ошибок» или «промахов»)

недопустимо, поэтому сначала необходимо исключить их.
Для выяснения, является ли некоторое наблюдение уq грубой ошибкой может быть применен один из статистических критериев.
Критерий Стьюдента
Опыт считается бракованным, если вычисленное значение критерия tP окажется по модулю больше табличного t. Значения t берутся из таблицы распределения Стьюдента.
Слайд 4ИСКЛЮЧЕНИЕ ГРУБЫХ ОШИБОК
где yumin , yumax - min и max из

всех полученных откликов в точке u и сравнивнить с табличным числом задавшись числом степеней свободы fu= n - 1 и уровнем значимости .
Слайд 5Проверка однородности построчных дисперсий
Цель проверки - определить, является ли измерение отклика во

всех точках равноточными или нет. Понятие однородности нескольких оценок дисперсий S12, S22 ... SN2 означает, что все величины Su2 являются оценками одной и той же дисперсии Sy2 - дисперсии воспроизводимости.
В этом случае различие между оценками S12, S22 ... SN2 объясняется их случайным характером.
Слайд 6Критерий Фишера
f1 = n1-1; f2 = n2-1.
Если F ≤ Fтаб ,

то дисперсии однородны, а измерения равноточны.
Слайд 7КРИТЕРИЙ КОХРЕНА
fu = n-1 fΣ = N.
Если Gр ≤ Gкр ,

то дисперсии однородны, а измерения равноточны.
Слайд 8ДИСПЕРСИЯ ВОСПРОИЗВОДИМОСТИ
где i = 1, 2, ..., N; q = 1,

2, ..., n.
Слайд 9ДИСПЕРСИЯ ВОСПРОИЗВОДИМОСТИ
Величина является оценкой СКО
σy и носит название ошибки опыта.
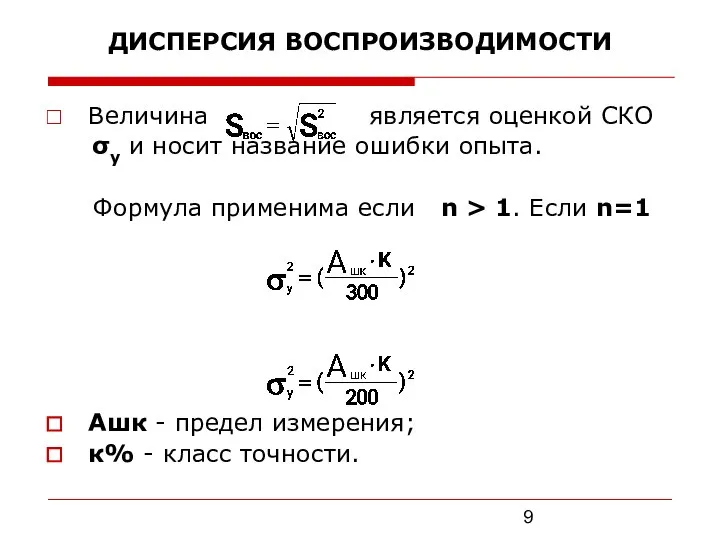
Формула применима если n > 1. Если n=1
Ашк - предел измерения;
к% - класс точности.
Слайд 10ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ bi
Использование МНК, являющегося основой регрессионного анализа, возможно при трех допущениях:
Отклик

подчиняется нормальному закону распределения.
Значения yui - статистически независимы.
Построчные дисперсии однородны.
С помощью указанных выражений получают статистически независимые коэффициенты bi. Поэтому количество их в уравнении регрессии можно увеличивать по мере необходимости. Включение новых коэффициентов не изменит значений ранее вычисленных.
Слайд 11ПРОВЕРКА СТАТИСТИЧЕСКОЙ ЗНАЧИМОСТИ КОЭФФИЦИЕНТОВ
Расчетное значение критерия Стьюдента
tpi ≤ tкр - коэффициент

статистически незначим и отбрасывается. tкр выбирается по таблицам исходя из уровня значимости α и числа степеней свободы
fi = N ( n-1 ).
На практике обычно для сокращения объема расчетов вычисляют не все значения tpi , а одно значение bкр. Все коэффициенты bi меньше bкр принимаются равными нулю.
Слайд 12ПРОВЕРКА СТАТИСТИЧЕСКОЙ ЗНАЧИМОСТИ КОЭФФИЦИЕНТОВ
bкр = Sbi ⋅ tкр












 Интерактивные тренинги по геометрии для подготовки к ОГЭ
Интерактивные тренинги по геометрии для подготовки к ОГЭ Прямой счет, обратный счет. Повторение
Прямой счет, обратный счет. Повторение Математический журнал Хочу все знать. Задачи на движение
Математический журнал Хочу все знать. Задачи на движение Преобразования графиков функций
Преобразования графиков функций Объем пирамиды
Объем пирамиды Построение сечений многогранников
Построение сечений многогранников Геометрический смысл производной. Решение примеров на геометрический смысл производной
Геометрический смысл производной. Решение примеров на геометрический смысл производной Признаки параллельности прямых
Признаки параллельности прямых Линейные пространства и линейные операторы. Лекция 3
Линейные пространства и линейные операторы. Лекция 3 Обработка результатов измерений при прямых однократных измерениях. Математические методы планирования активного эксперимента
Обработка результатов измерений при прямых однократных измерениях. Математические методы планирования активного эксперимента Интеграл
Интеграл Презентация на тему Правильные и неправильные дроби
Презентация на тему Правильные и неправильные дроби  Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ
Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ Преподаватель математики и информатики ГБОУ СПО РО «Константиновский педагогический колледж» Алексей Юлия Вадимовна
Преподаватель математики и информатики ГБОУ СПО РО «Константиновский педагогический колледж» Алексей Юлия Вадимовна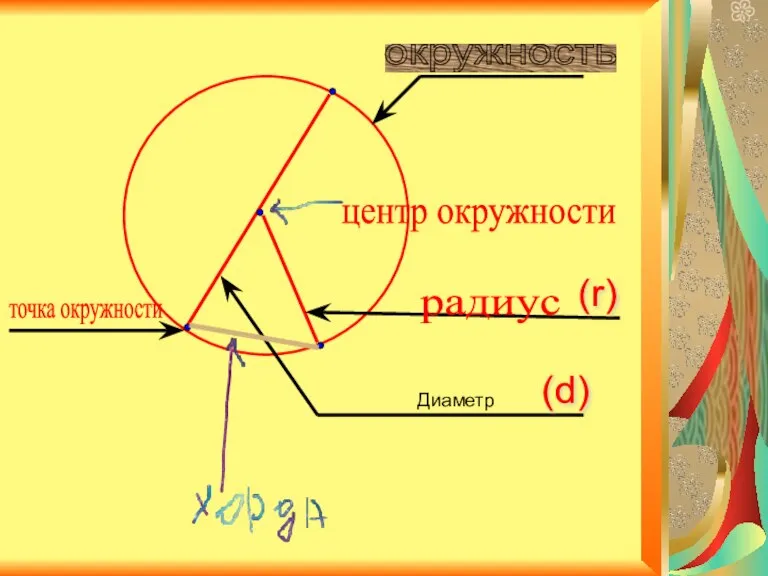 Окружность
Окружность Презентация на тему Формулы сокращённого умножения
Презентация на тему Формулы сокращённого умножения  Методы оптимизации
Методы оптимизации Четырёхугольник
Четырёхугольник Додекаэдр
Додекаэдр Естественно-математическое ралли!!!!
Естественно-математическое ралли!!!! Длина окружности и ее частей
Длина окружности и ее частей Построение треугольника
Построение треугольника Деление двузначных чисел
Деление двузначных чисел Четырёхугольники
Четырёхугольники Свойства логарифмов положительного числа
Свойства логарифмов положительного числа Связь между параллельностью и перпендикулярностью прямых и плоскостей (Задание)
Связь между параллельностью и перпендикулярностью прямых и плоскостей (Задание) Демо версия. Математика 2.3
Демо версия. Математика 2.3