Параллельность в пространстве

Оглавление
Параллельные прямые в пространстве.
Параллельность трех прямых.
Параллельность прямой и плоскости.
Параллельность плоскостей.
Свойства параллельных плоскостей.

Параллельные прямые в пространстве
Определение
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Обозначение
а ιι b
с ιι d

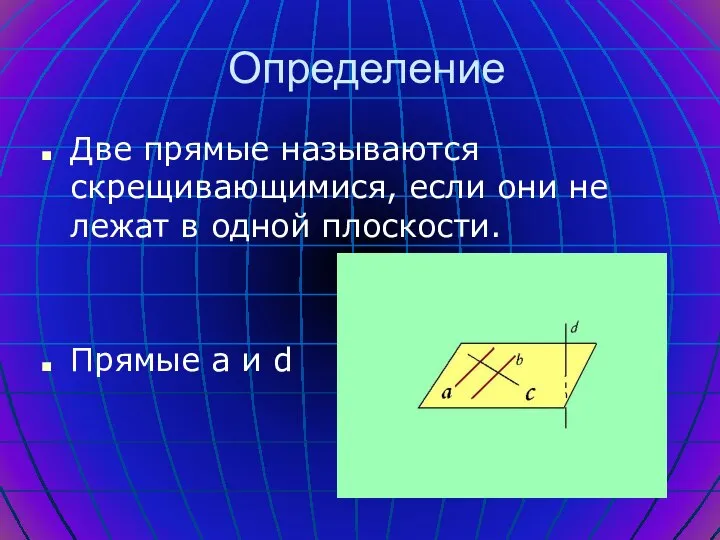
Определение
Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Прямые a и d

Теорема
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и причем только одна.

Параллельность отрезков, отрезка и прямой,лучей.
Два отрезка называются параллельными, если они лежат на параллельных прямых.
Отрезок и прямая называются параллельными, если они лежат на параллельных прямых.
Два луча называются параллельными, если они лежат на параллельных прямых.

Лемма
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

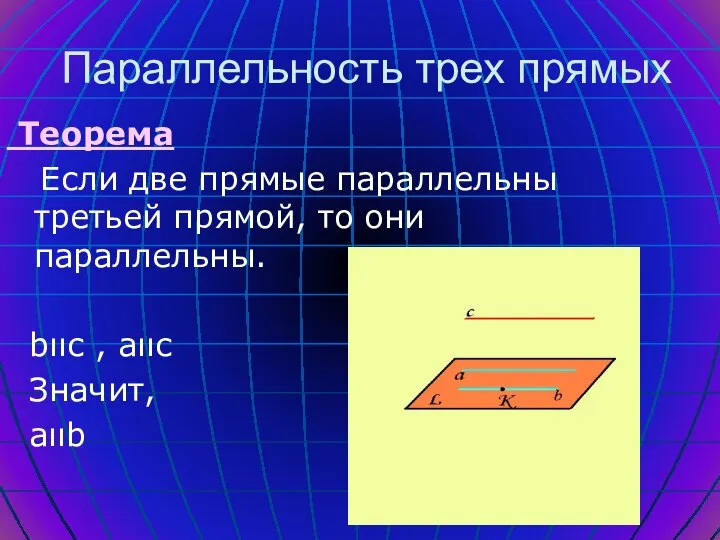
Теорема
Если две прямые параллельны третьей прямой, то они параллельны.
bιιс , аιιс
Значит,
аιιb
Параллельность трех прямых

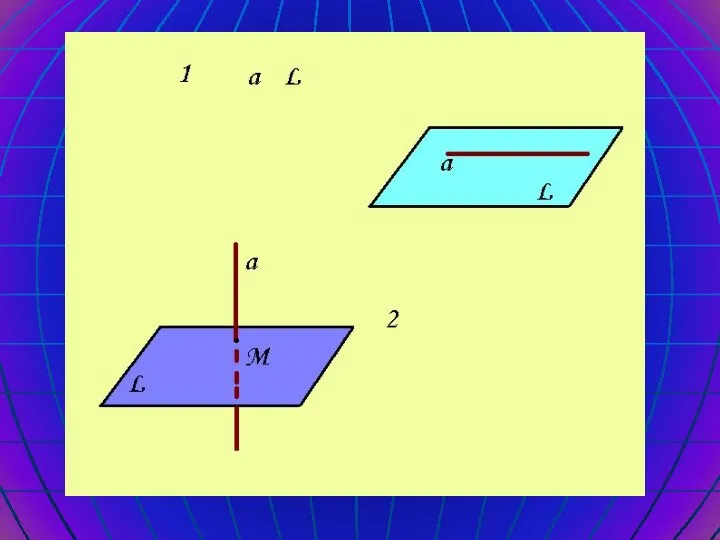
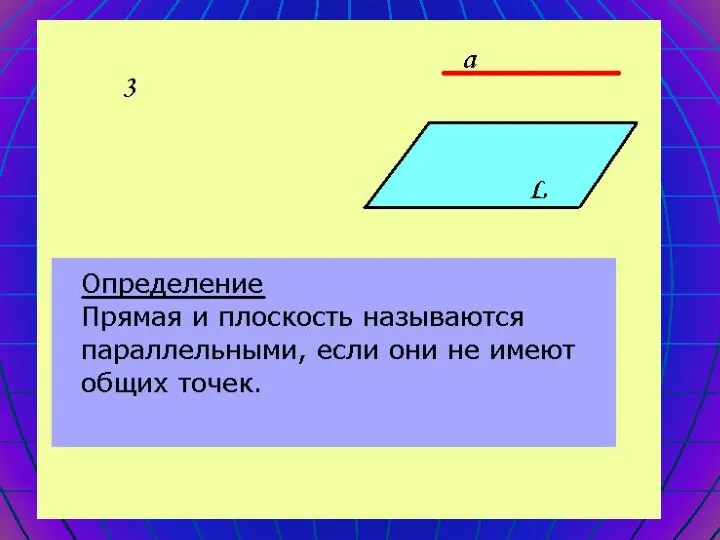
Параллельность прямой и плоскости
Возможны три случая взаимного расположения прямой и плоскости в пространстве:
Прямая лежит в плоскости.
Прямая и плоскость имеют только одну точку.
Прямая и плоскость не имеют общих точек.

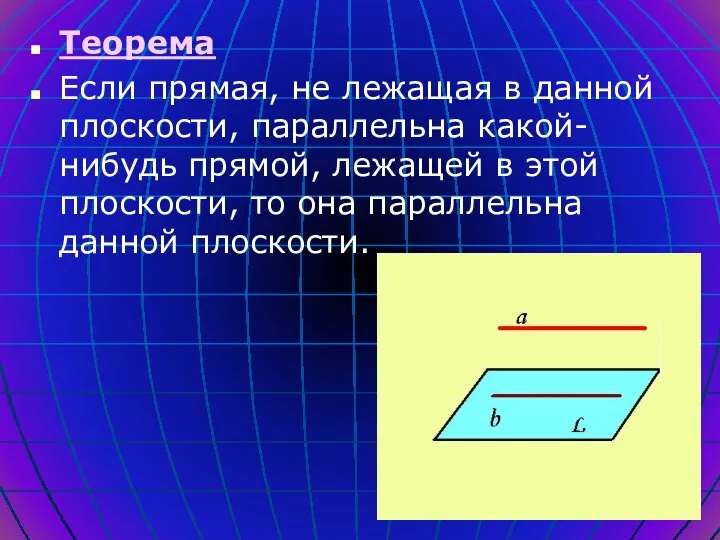
Теорема
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Следствие
Если плоскость проходит через данную прямую параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

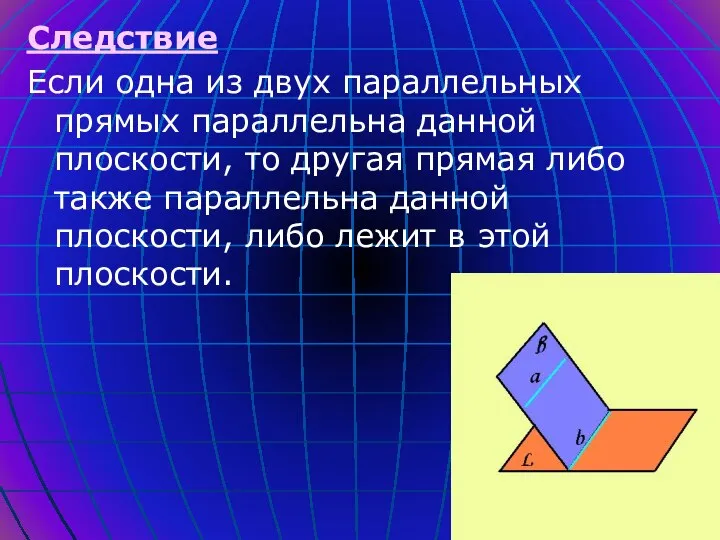
Следствие
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Параллельность плоскостей

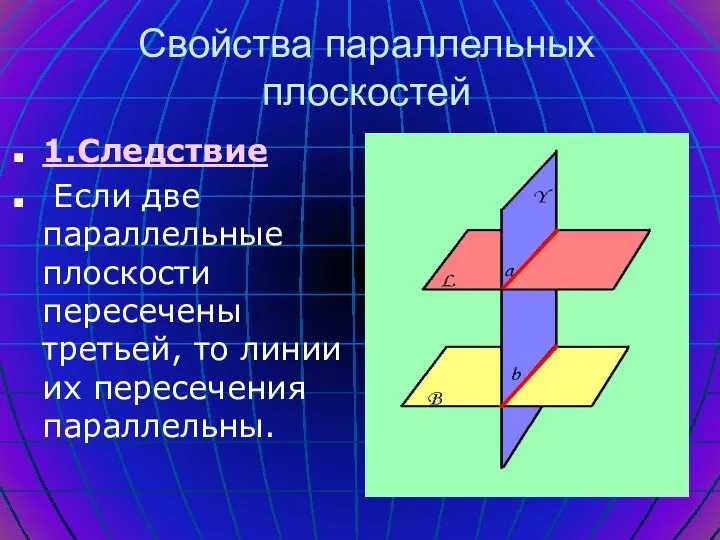
Свойства параллельных плоскостей
1.Следствие
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.