Перпендикуляр и наклонная

ЦЕЛИ УРОКА:
ВВЕСТИ ПОНЯТИЕ
РАССТОЯНИЕОТ ТОЧКИ ДО ПРЯМОЙ
РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
РАССТОЯНИЕ МЕЖДУ ПРЯМОЙ И ПАРАЛЛЕЛЬНОЙ ЕЙ ПЛОСКОСТЬЮ
РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
ДОКАЗАТЬ ТЕОРЕМУ О ТРЕХ ПЕРПЕНДИКУЛЯРАХ
НАУЧИТСЯ ПРИМЕНЯТЬ ТЕОРЕМУ О ТРЕХ ПЕРПЕНДИКУЛЯРАХ ПРИ РЕШЕНИИ ЗАДАЧ

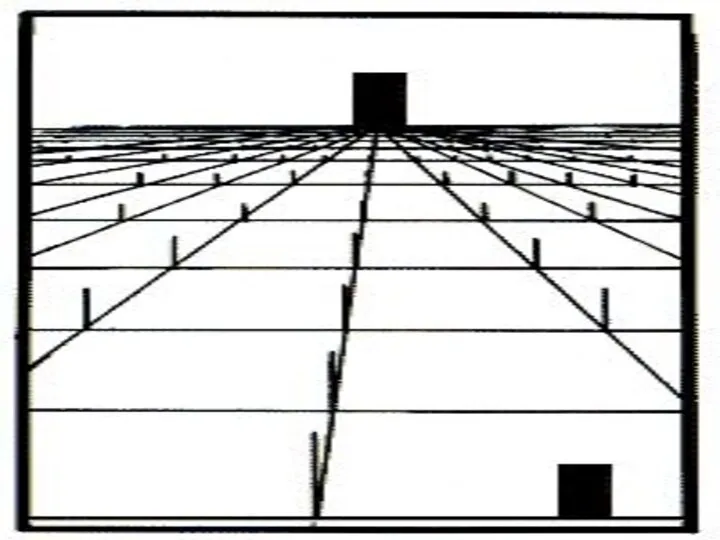
Иллюстрациями каких теорем могли бы быть следующие картинки?
Итак, приступим к делу!

Одно из красивейших произведений древнегреческой архитектуры – Парфенон (V в. до н. э.).

А
В
С
Назовите гипотенузу прямоугольного треугольника АВС.
Сравните катет и гипотенузу прямоугольного треугольника. Что больше и почему?
Сформулируйте теорему Пифагора.
Какие прямые называются перпендикулярными?
Верно ли утверждение: «прямая перпендикулярна плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости».
Продолжи предложение: «Прямая перпендикулярна плоскости, если она . . . »
ПОВТОРИТЕ!

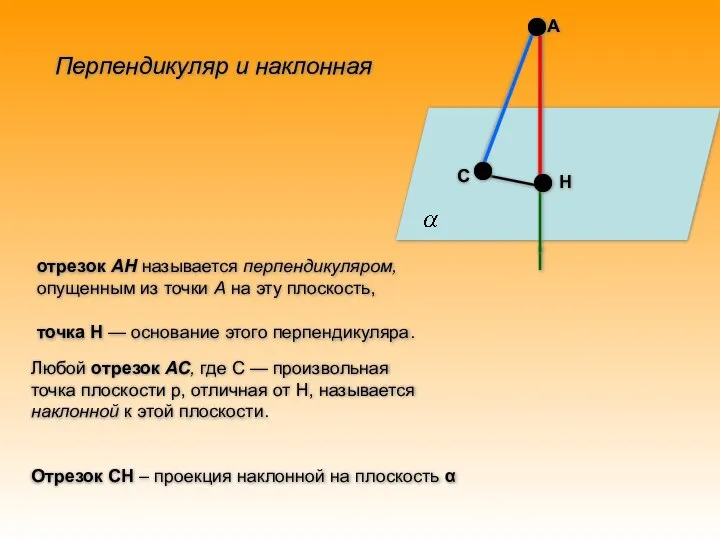
А
Н
С
отрезок АН называется перпендикуляром, опущенным из точки А на эту плоскость,
точка Н — основание этого перпендикуляра.
Любой отрезок АС, где С — произвольная точка плоскости p, отличная от Н, называется наклонной к этой плоскости.
Отрезок СН – проекция наклонной на плоскость α
Перпендикуляр и наклонная

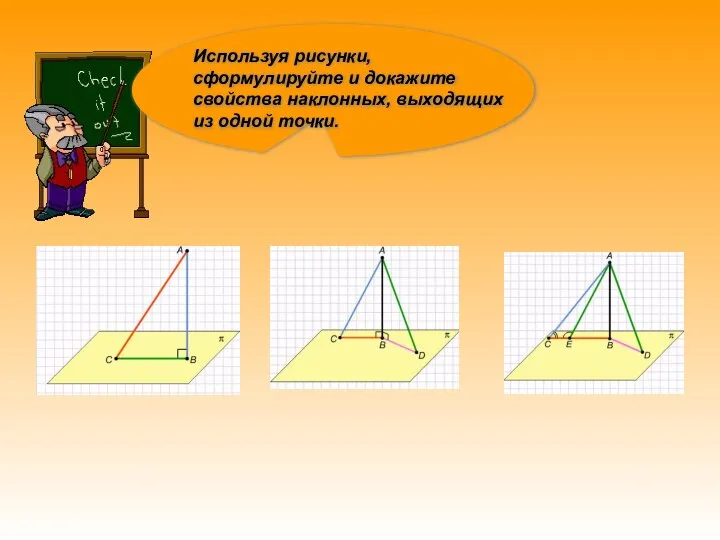
Используя рисунки, сформулируйте и докажите свойства наклонных, выходящих из одной точки.

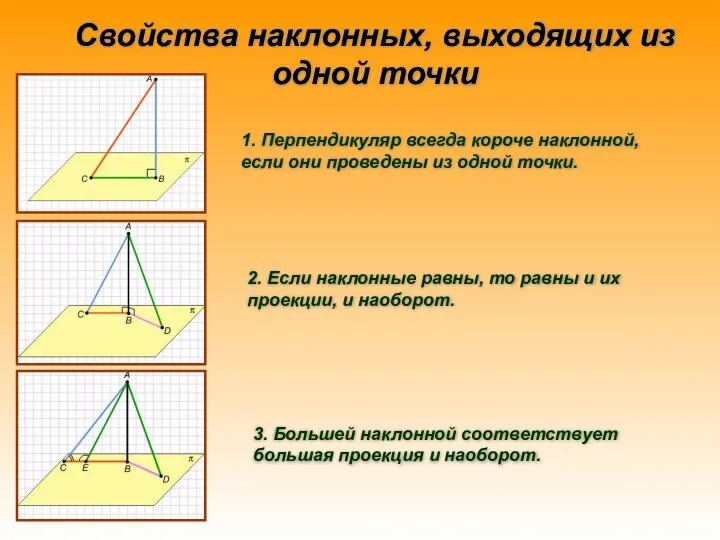
Свойства наклонных, выходящих из одной точки
1. Перпендикуляр всегда короче наклонной, если они проведены из одной точки.
2. Если наклонные равны, то равны и их проекции, и наоборот.
3. Большей наклонной соответствует большая проекция и наоборот.

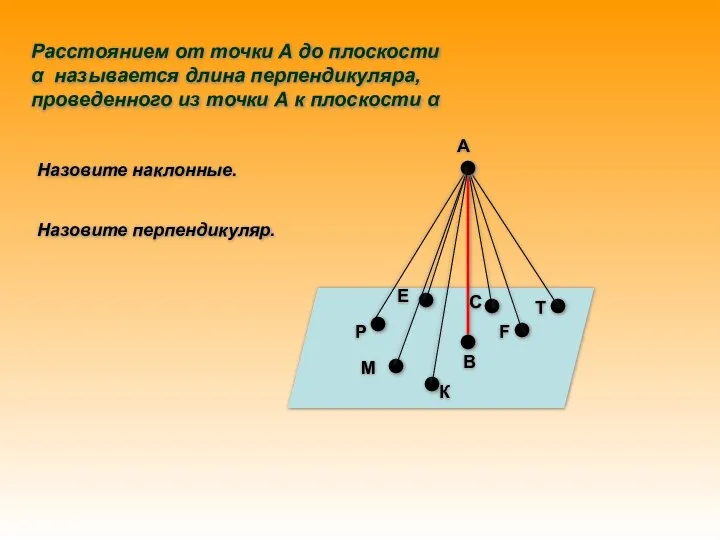
А
М
В
С
К
Р
Е
Т
F
Расстоянием от точки А до плоскости α называется длина перпендикуляра, проведенного из точки А к плоскости α
Назовите наклонные.
Назовите перпендикуляр.

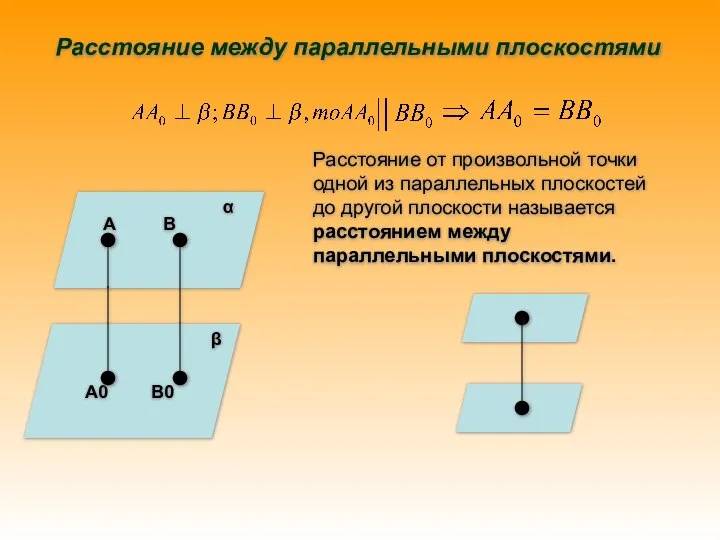
α
β
А
А0
В
В0
Расстояние между параллельными плоскостями
Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями.

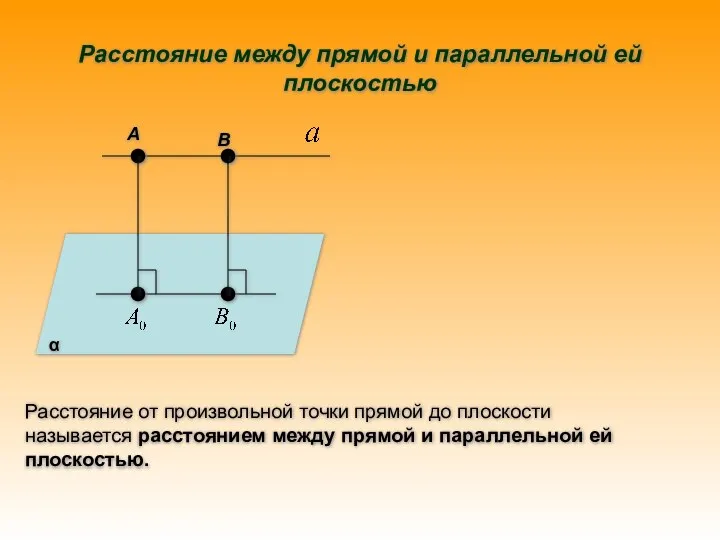
α
А
В
Расстояние между прямой и параллельной ей плоскостью
Расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.

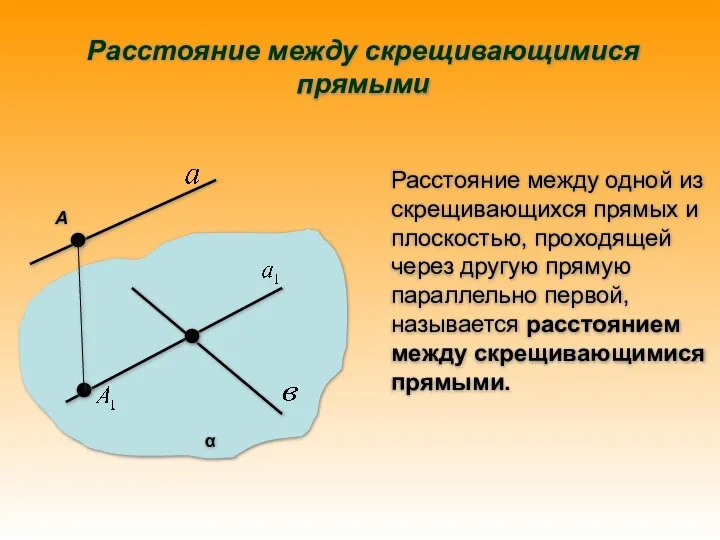
α
А
Расстояние между скрещивающимися прямыми
Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

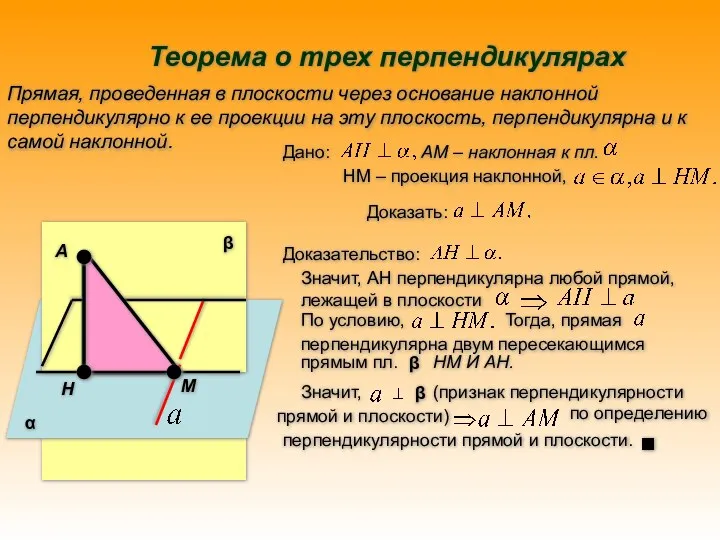
Теорема о трех перпендикулярах
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
Дано:
АМ – наклонная к пл.
НМ – проекция наклонной,
Доказать:
А
Н
М
α
β
Доказательство:
Значит, АН перпендикулярна любой прямой, лежащей в плоскости
По условию,
Тогда, прямая
перпендикулярна двум пересекающимся
прямым пл.
β
Значит,
β
(признак перпендикулярности
прямой и плоскости)
по определению
перпендикулярности прямой и плоскости.
НМ И АН.

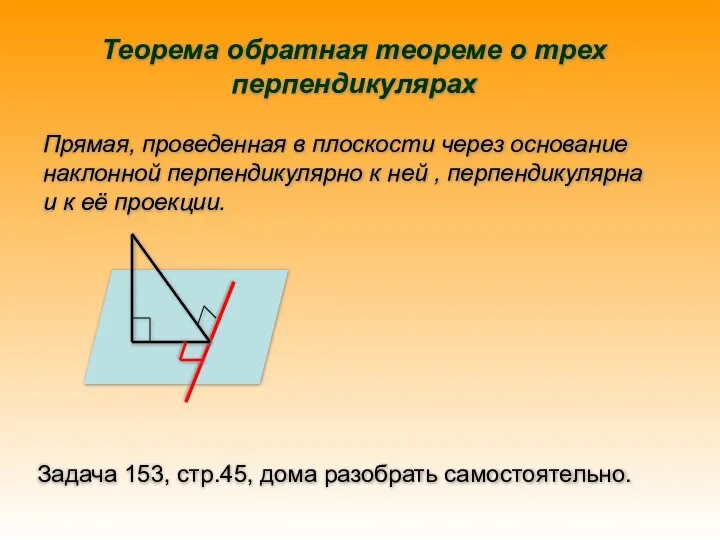
Теорема обратная теореме о трех перпендикулярах
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней , перпендикулярна и к её проекции.
Задача 153, стр.45, дома разобрать самостоятельно.

А теперь задача