Содержание
- 2. Первообразная Функция F(x)называется первообразной для функции f(x)на некотором промежутке, если для всех x из этого промежутка
- 4. Основное свойство первообразных Если F(x)– первообразная для функции f(x) на некотором промежутке, то функция F(x)+C также
- 5. Таблица первообразных f(x) F(x) F(x)
- 7. Три правила нахождения первообразных Если F(x) есть первообразная для f(x), а G(x) – первообразная для g(x),
- 8. Если F(x) есть первообразная для f(x), а k – постоянная, то функция kF(x) есть первообразная для
- 10. Скачать презентацию







 Решение задач
Решение задач Функции нескольких переменных. Частные производные. Полный дифференциал функции. Лекция 18
Функции нескольких переменных. Частные производные. Полный дифференциал функции. Лекция 18 Корень п-ой степени
Корень п-ой степени Диаметр линии второго порядка
Диаметр линии второго порядка Тестирование МЦКО. Задания с развернутым ответом. (7 класс)
Тестирование МЦКО. Задания с развернутым ответом. (7 класс) Интегральное исчисление
Интегральное исчисление Презентация на тему Деление многозначного числа на однозначное
Презентация на тему Деление многозначного числа на однозначное 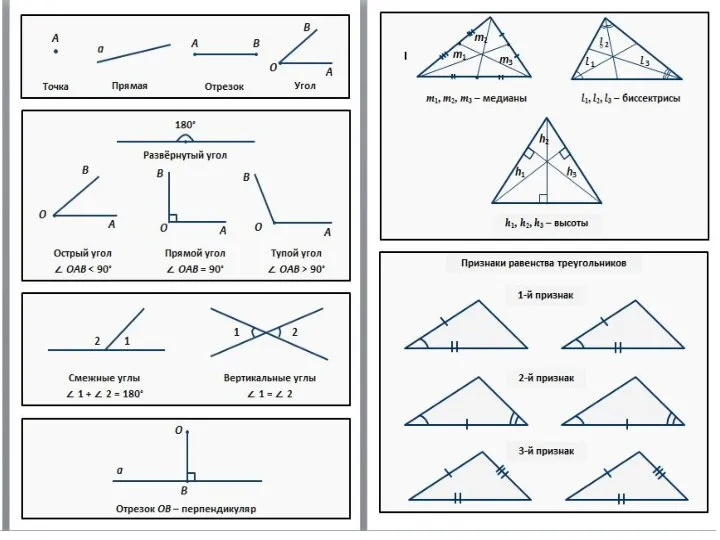 Геометрия. 8 класс
Геометрия. 8 класс Визуальный и измерительный контроль
Визуальный и измерительный контроль Конус – тело вращения
Конус – тело вращения Решение уравнений третьей степени
Решение уравнений третьей степени Lektsia_po_modulnoi_774_edinitse_4_Pervoobraznaya_i_neopredelennyi_774_integral_Metody_integrirovania
Lektsia_po_modulnoi_774_edinitse_4_Pervoobraznaya_i_neopredelennyi_774_integral_Metody_integrirovania Построение сечений
Построение сечений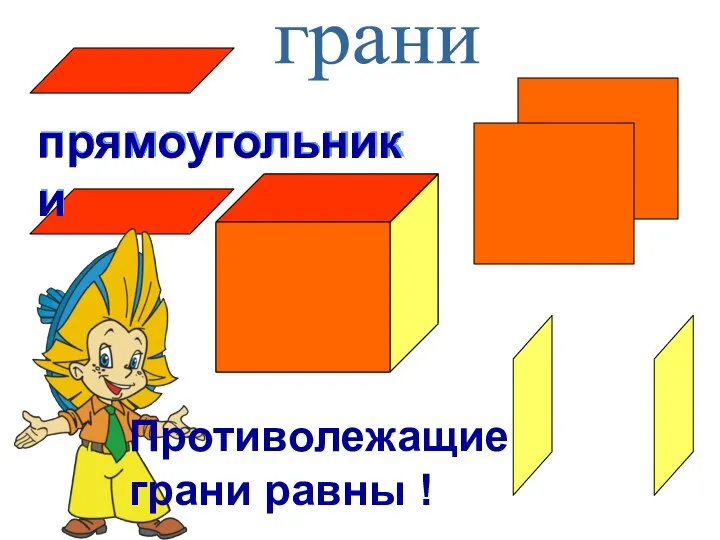 Прямоугольники. Противолежащие грани (развертка № 17)
Прямоугольники. Противолежащие грани (развертка № 17) Презентация на тему Лист Мебиуса
Презентация на тему Лист Мебиуса  Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3
Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3 Усеченый конус
Усеченый конус ЦАРСКОЙ ДОРОГИ В МАТЕМАТИКЕ НЕТ.
ЦАРСКОЙ ДОРОГИ В МАТЕМАТИКЕ НЕТ. Градиент. Производная по направлению
Градиент. Производная по направлению Куб и шар
Куб и шар Умножение дробей. Анаграммы
Умножение дробей. Анаграммы Дюжина задач на параметры
Дюжина задач на параметры Золотое сечение
Золотое сечение Числовая окружность в координатной плоскости
Числовая окружность в координатной плоскости Показательная функция
Показательная функция Возможности символьного вычисления в среде MatLab
Возможности символьного вычисления в среде MatLab Алгоритм исследования функции
Алгоритм исследования функции Решение задач по теме Смежные и вертикальные углы. Перпендикулярные прямые
Решение задач по теме Смежные и вертикальные углы. Перпендикулярные прямые