Содержание
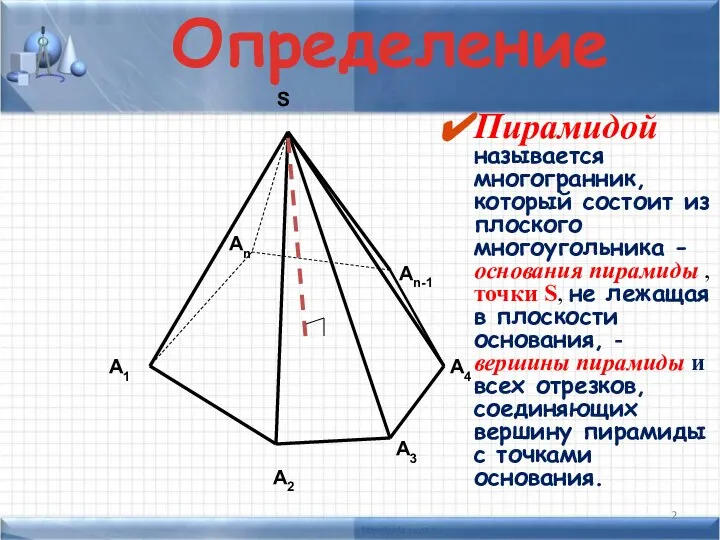
- 2. А1 А2 А3 А4 Аn Аn-1 S Пирамидой называется многогранник, который состоит из плоского многоугольника -
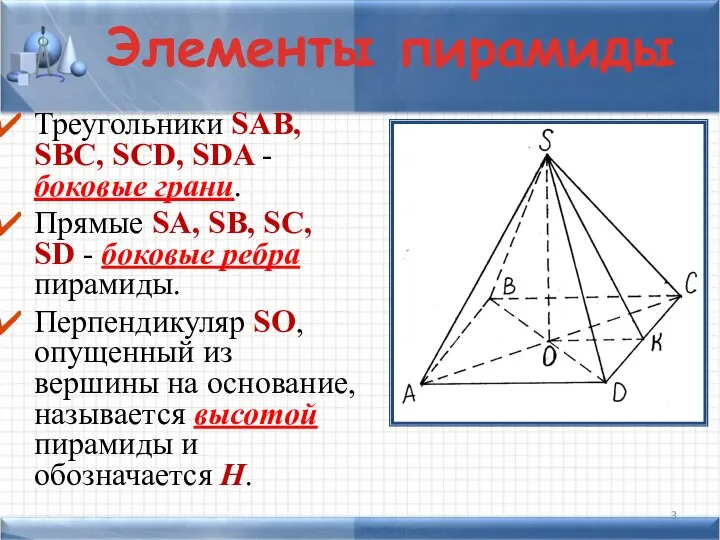
- 3. Треугольники SAB, SBC, SCD, SDA - боковые грани. Прямые SA, SB, SC, SD - боковые ребра
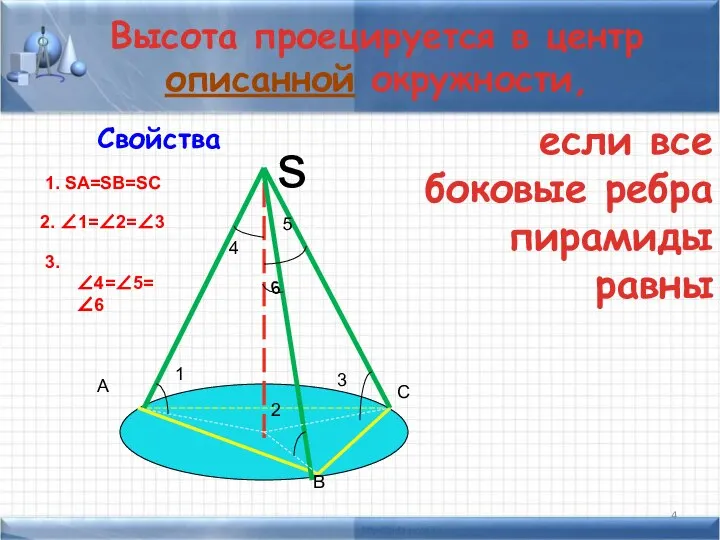
- 4. Высота проецируется в центр описанной окружности, Свойства s A B C 1 2 3 6 4
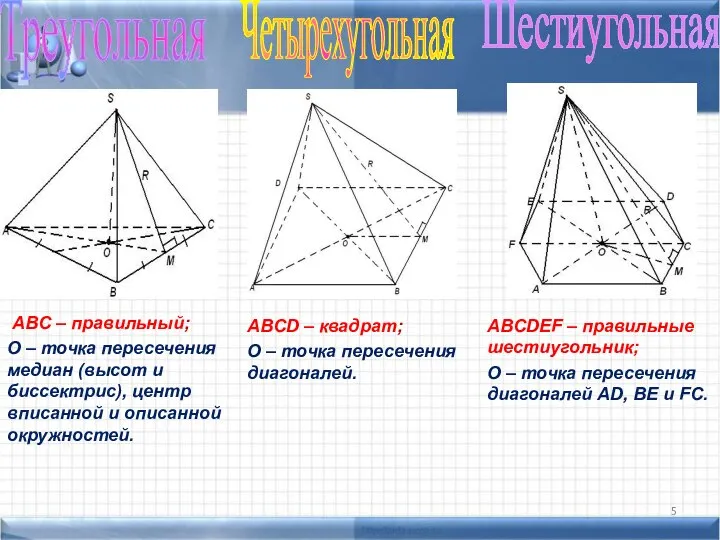
- 5. Треугольная Четырехугольная Шестиугольная
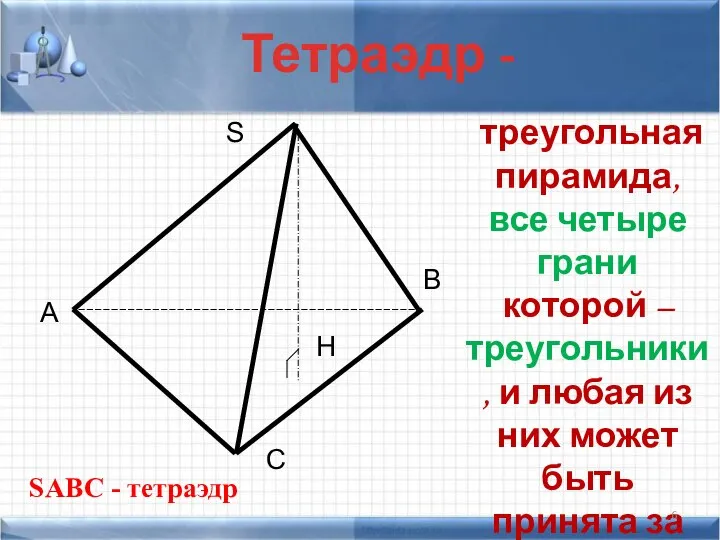
- 6. Тетраэдр - A B C S H SABC - тетраэдр треугольная пирамида, все четыре грани которой
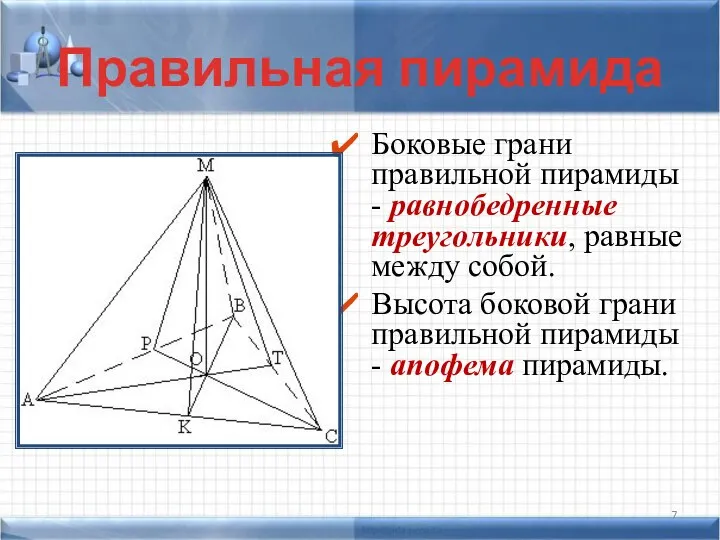
- 7. Боковые грани правильной пирамиды - равнобедренные треугольники, равные между собой. Высота боковой грани правильной пирамиды -
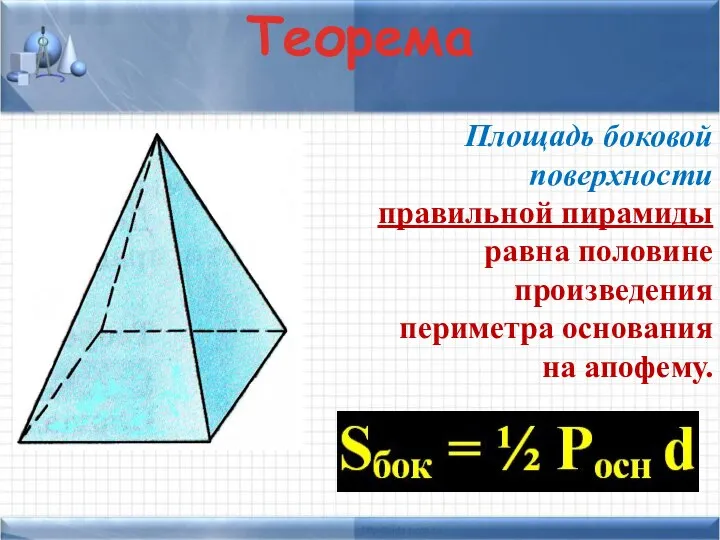
- 8. Теорема Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
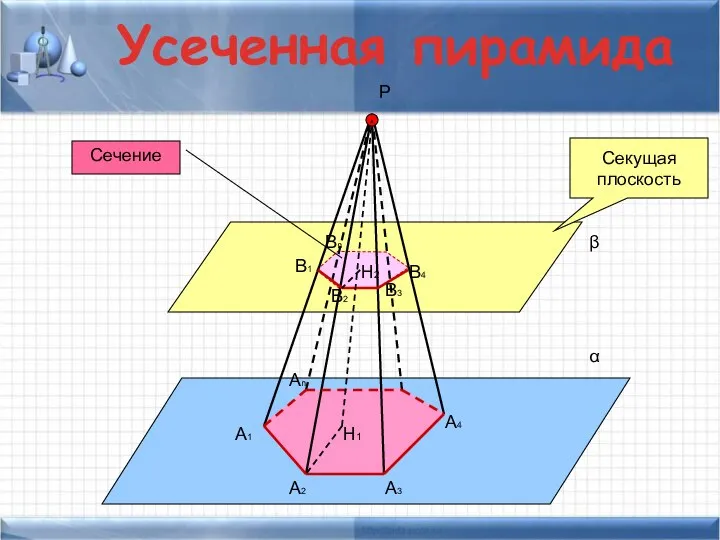
- 9. A1 α β A2 A3 An A4 P В3 В1 В2 В4 Вn Секущая плоскость Сечение
- 10. Задание
- 12. Скачать презентацию

 Индивидуальный проект на тему Золотое сечение в природе
Индивидуальный проект на тему Золотое сечение в природе Решите примеры
Решите примеры Первообразная и интеграл
Первообразная и интеграл Математический факультатив
Математический факультатив Промежуточная мерка
Промежуточная мерка Красота многогранников и не только. Из природы в науку
Красота многогранников и не только. Из природы в науку Расстояние между точками
Расстояние между точками Матрицы и определители
Матрицы и определители Первообразная. 11 класс
Первообразная. 11 класс Метод координат. Нахождение углов
Метод координат. Нахождение углов Уравнение с параметром
Уравнение с параметром Построение графиков функций с помощью геометрических преобразований
Построение графиков функций с помощью геометрических преобразований Аксиомы стереометрии и следствия из них
Аксиомы стереометрии и следствия из них Теорема Пифагора
Теорема Пифагора Определение и признаки параллелограмма
Определение и признаки параллелограмма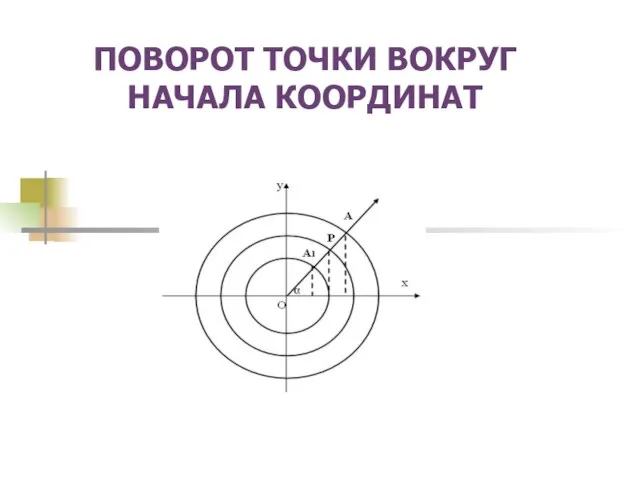 ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ Прибавить и вычесть 3. Решение текстовых задач. Урок №57
Прибавить и вычесть 3. Решение текстовых задач. Урок №57 Несобственные интегралы первого рода
Несобственные интегралы первого рода Многогранники
Многогранники Свойство биссектрисы угла. Свойства серединного перпендикуляра к отрезку
Свойство биссектрисы угла. Свойства серединного перпендикуляра к отрезку Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Модели статистического прогнозирования. Урок 31
Модели статистического прогнозирования. Урок 31 Признак перпендикулярности плоскостей
Признак перпендикулярности плоскостей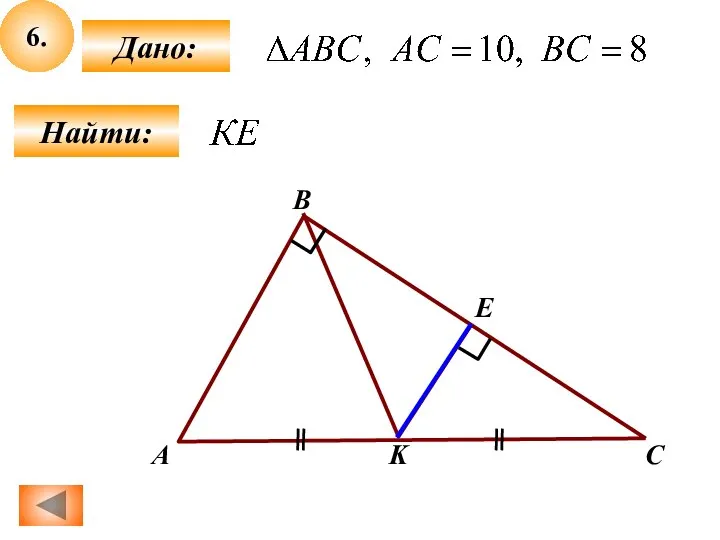 Задачи по геометрии (6-7)
Задачи по геометрии (6-7) Модуль. Определение. Свойства. Геометрический смысл модуля
Модуль. Определение. Свойства. Геометрический смысл модуля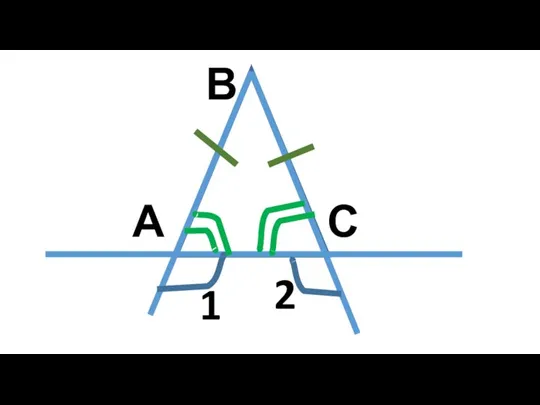 Равнобедренный треугольник
Равнобедренный треугольник Уравнения. 3 класс
Уравнения. 3 класс