Планиметрия и стериометрия

Геометрия
Планиметрия
Стереометрия

Планиметрия
Планиметрия — раздел геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости. Фигуры, изучаемые планиметрией:
Точка
Прямая
Параллелограмм (частные случаи Квадрат, Прямоугольник, Ромб)
Трапеция
Окружность
Треугольник
Многоугольник

Аксиомы планиметрии
1. Аксиомы принадлежности
1.1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
1.2. Через любые две точки можно провести прямую, и только одну.

2. Аксиомы расположения
2.1. Из трех точек на прямой одна и только одна лежит между двумя друг
2.2. Прямая разбивает плоскость на две полуплоскости.

3. Аксиомы измерения
3.1. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумму длин частей, на которые он разбивается любой его точкой.
3.2. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180 градусов. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

4. Аксиомы откладывания
4.1. На любой полупрямой от ее начальной точки можно отложить отрезок, заданной длины, и только один.
4.2. От любой полупрямой в заданную полуплоскость можно отложить угол заданной градусной мерой, меньшей 180 градусов, и только один.
4.3. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

5. Аксиома параллельности
5.1. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

Стереометрия -
раздел геометрии, в котором
изучаются свойства фигур в
пространстве.

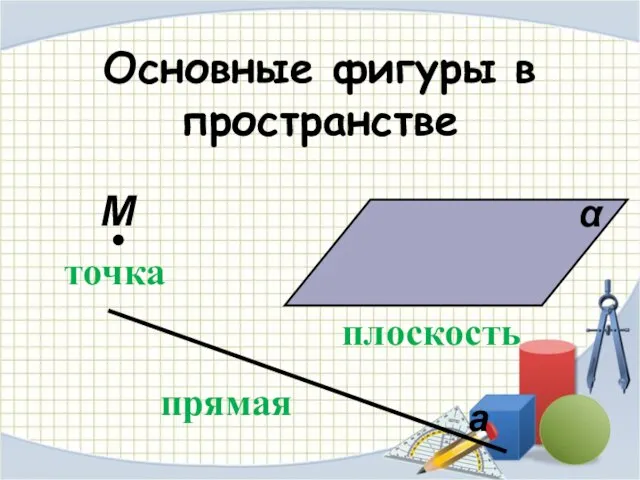
Основные фигуры в пространстве
точка
прямая
плоскость
М
α
а

Аксиомы стереометрии
и их следствия
Аксиома 1.
Аксиома 2.
Аксиома 3.
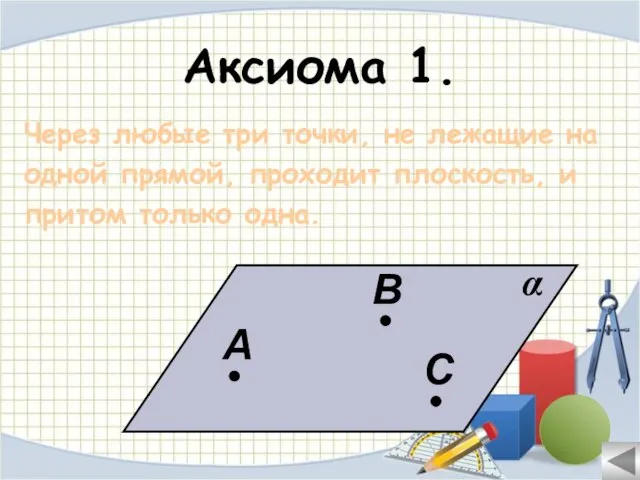
Следствие 1. Следствие 2.

Аксиома 1.
Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и
притом только одна.
α
А
В
С

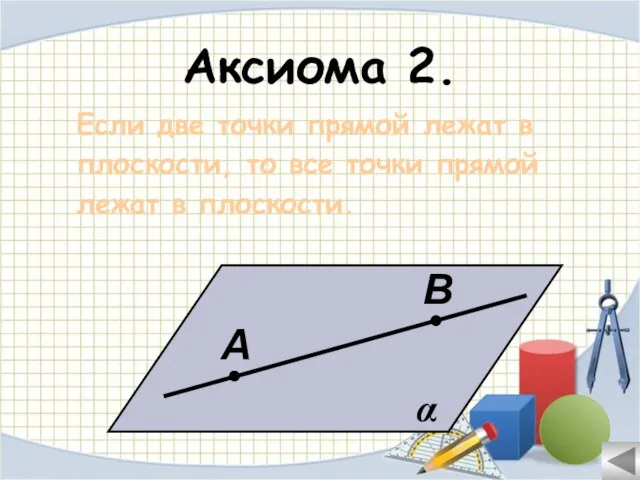
Аксиома 2.
Если две точки прямой лежат в
плоскости, то все точки прямой
лежат в плоскости.
α
А
В

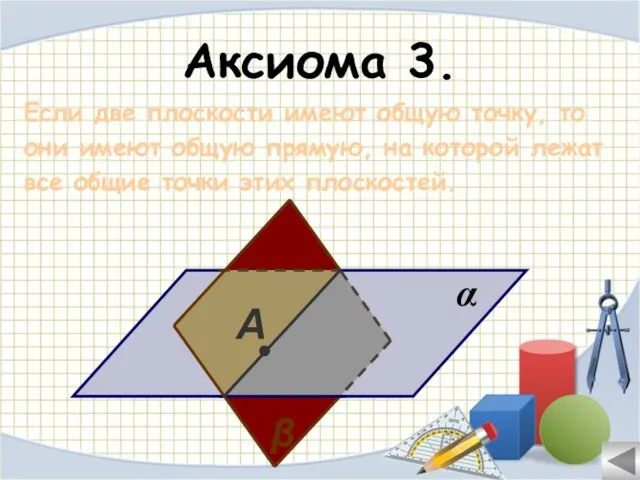
Аксиома 3.
Если две плоскости имеют общую точку, то
они имеют общую прямую, на которой лежат
все общие точки этих плоскостей.
α
А

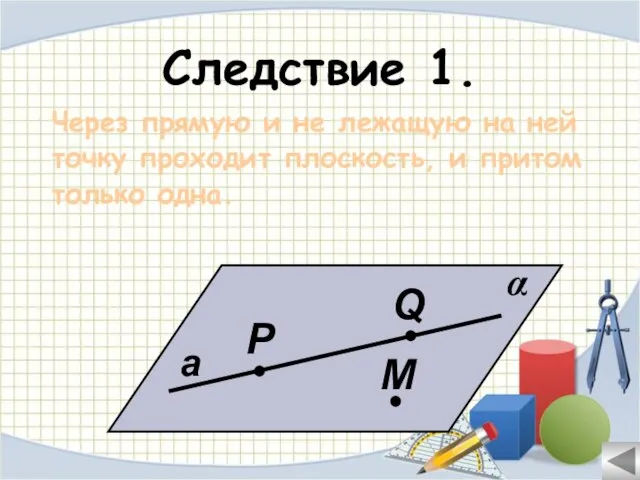
Следствие 1.
Через прямую и не лежащую на ней
точку проходит плоскость, и притом
только одна.
α
P
М
а
Q

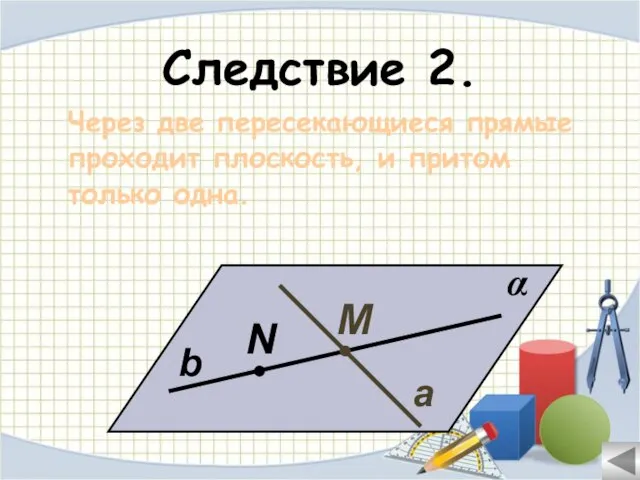
Следствие 2.
Через две пересекающиеся прямые
проходит плоскость, и притом
только одна.
α
N
М
b
a