Содержание
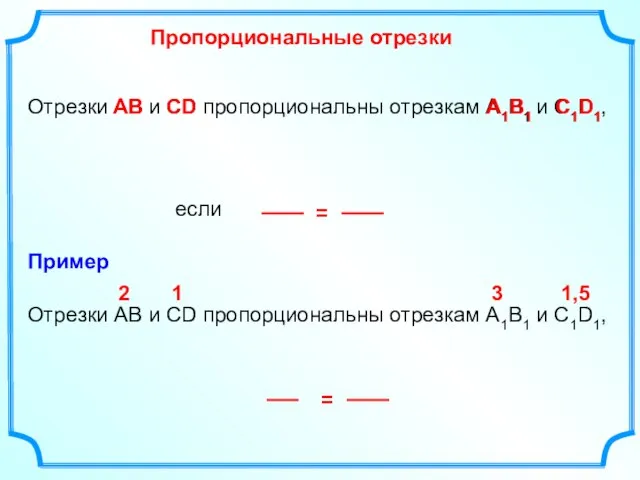
- 2. Отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1, если Пропорциональные отрезки АВ СD А1В1 C1D1
- 3. Отрезки АВ, СD и EF пропорциональны отрезкам А1В1, С1D1 и E1F1, если Понятие пропорциональности вводится и
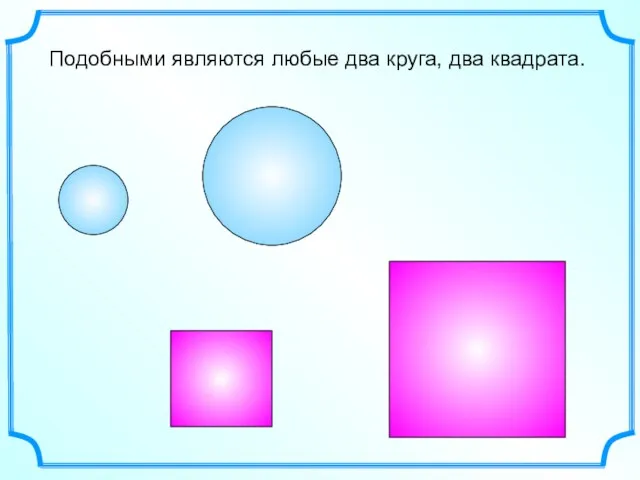
- 4. Подобными являются любые два круга, два квадрата.
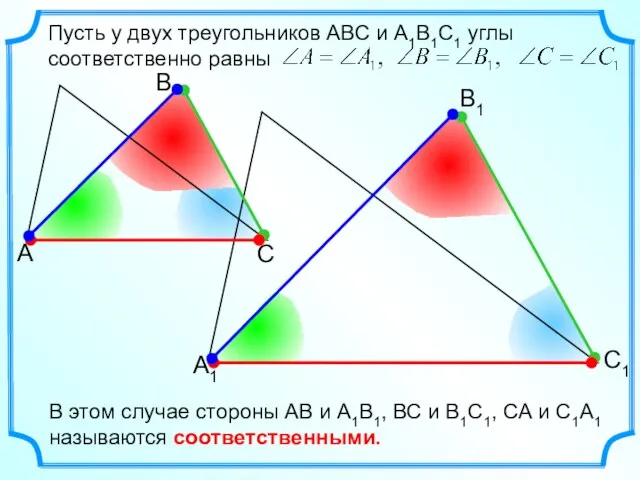
- 5. Пусть у двух треугольников АВС и А1В1С1 углы соответственно равны В этом случае стороны АВ и
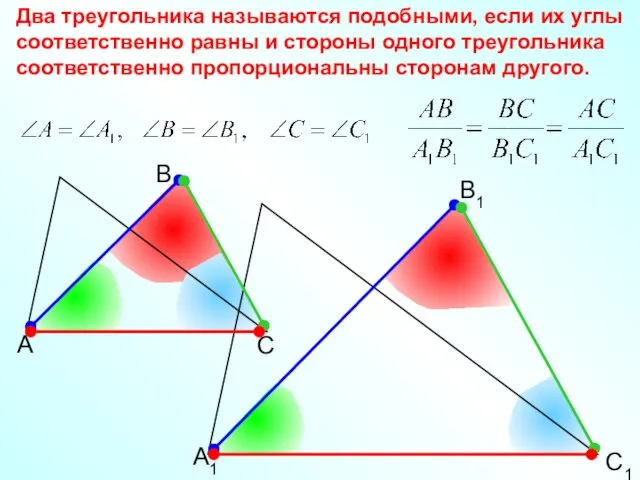
- 6. А В С С1 В1 А1 Два треугольника называются подобными, если их углы соответственно равны и
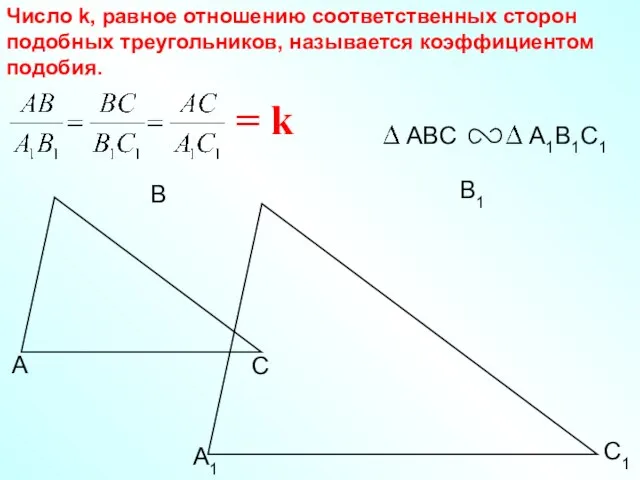
- 7. С1 В1 А1 Число k, равное отношению соответственных сторон подобных треугольников, называется коэффициентом подобия. = k
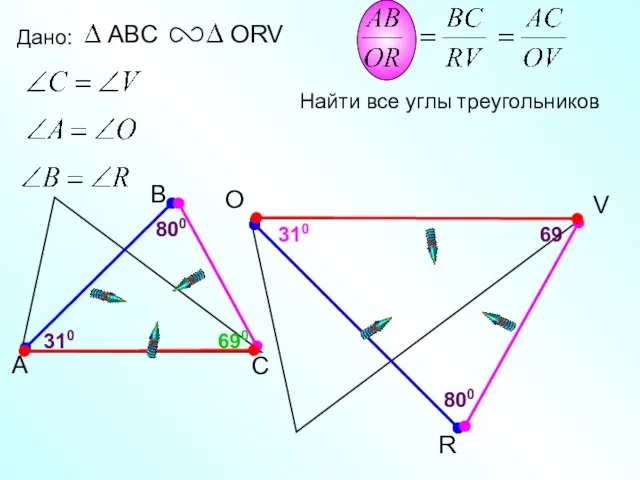
- 8. O R Дано: V 69 310 310 690 Найти все углы треугольников
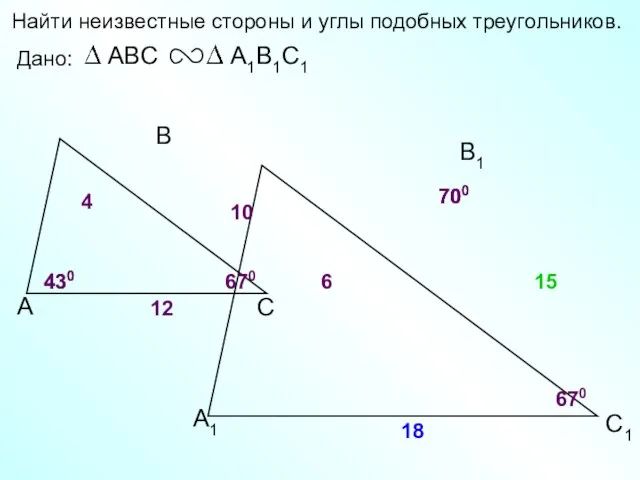
- 9. А В С С1 В1 А1 Найти неизвестные стороны и углы подобных треугольников. Дано: 430 700
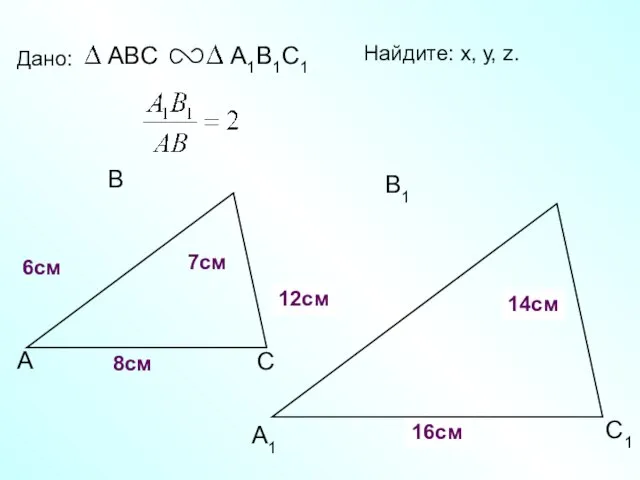
- 10. А В С С1 В1 А1 Дано: 6см 7см 8см Найдите: х, у, z. х у
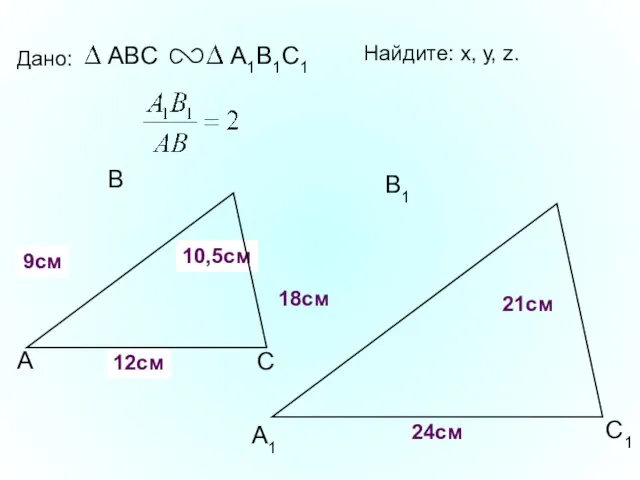
- 11. А В С С1 В1 А1 Дано: 18см 21см 24см Найдите: х, у, z. х у
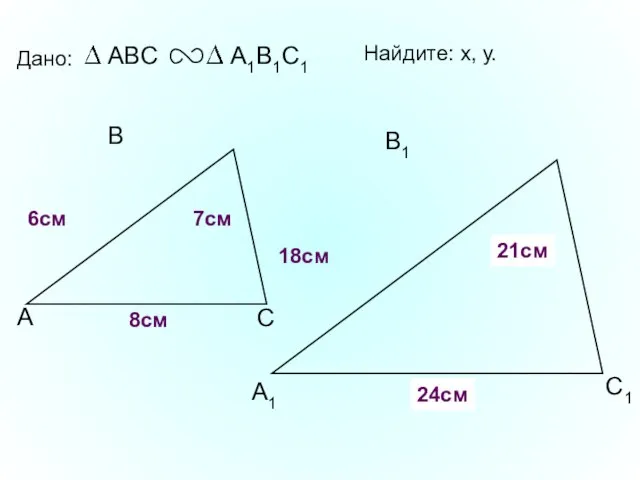
- 12. А В С С1 В1 А1 Дано: 18см 7см 6см Найдите: х, у. х у 21см
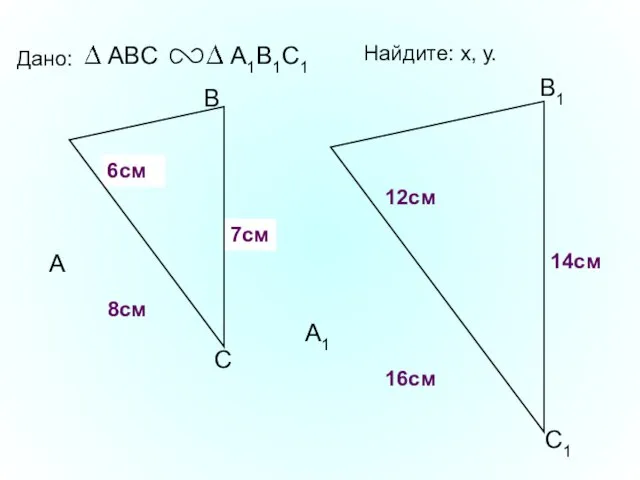
- 13. А В С С1 В1 А1 Дано: 16см 14см 8см Найдите: х, у. х у 7см
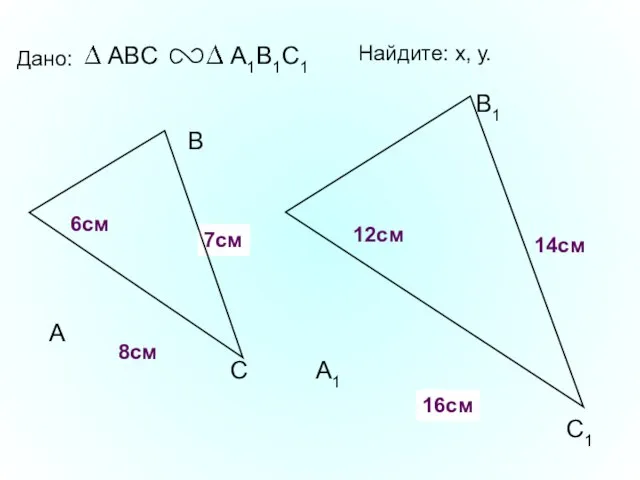
- 14. А В С С1 В1 А1 Дано: 12см 14см 6см Найдите: х, у. х у 7см
- 15. А С С1 В1 А1 Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. В =
- 16. Отношение периметров двух подобных треугольников равно коэффициенту подобия. +
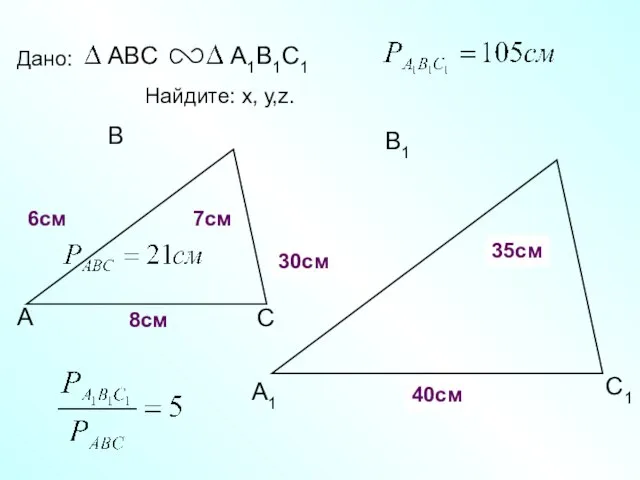
- 17. А В С С1 В1 А1 Дано: 7см 6см Найдите: х, у,z. х z 40см 8см
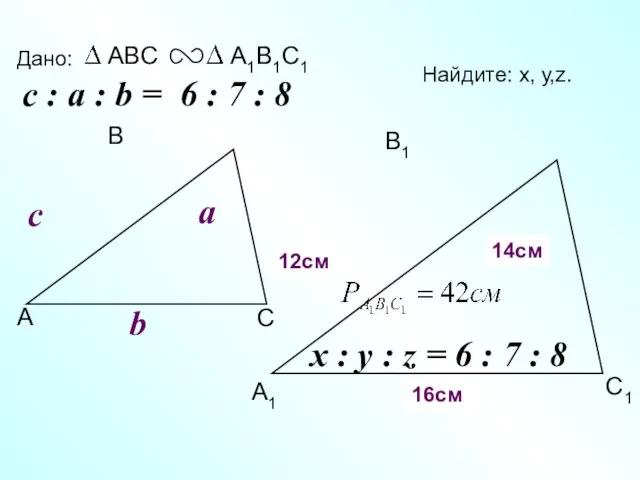
- 18. А В С С1 В1 А1 Дано: c Найдите: х, у,z. х z 16см y 12см
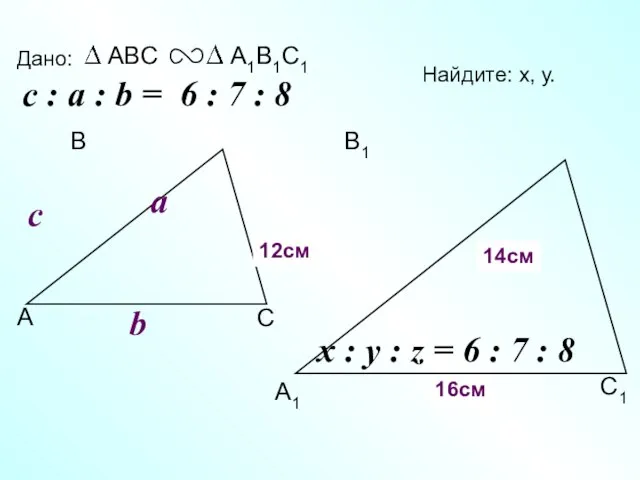
- 19. А В С С1 В1 А1 Дано: c Найдите: х, у. х 16см y 12см 14см
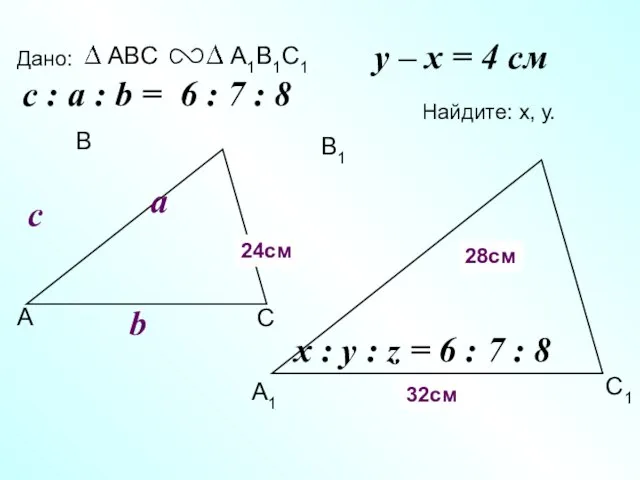
- 20. А В С С1 В1 А1 Дано: c Найдите: х, у. х y 24см 28см c
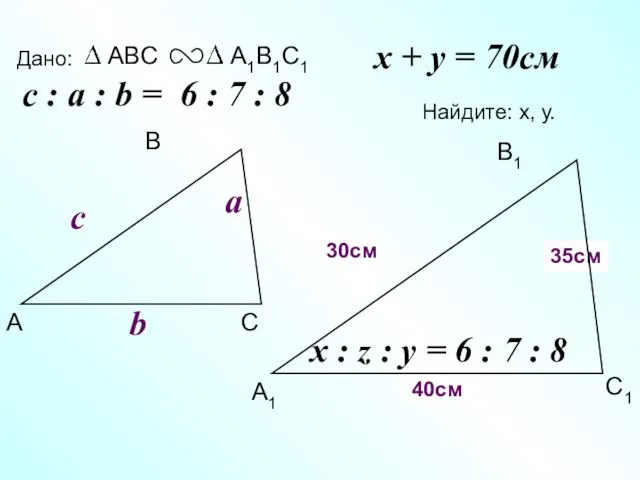
- 21. А В С С1 В1 А1 Дано: c Найдите: х, у. х Z 30см 35см c
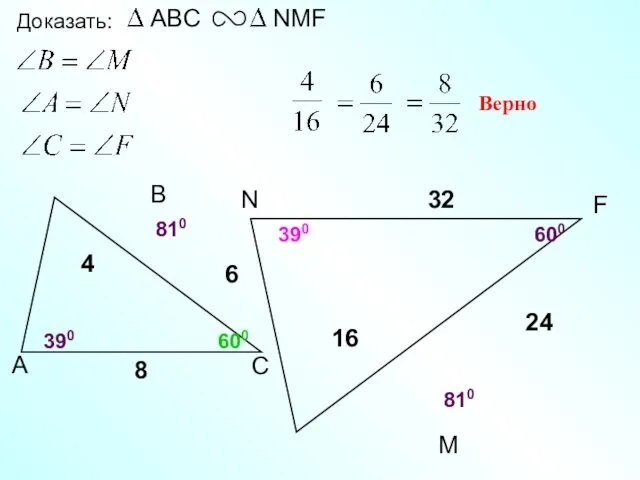
- 22. N 32 М Доказать: Верно 6 4 8 16 24 F 810 600 810 390 390
- 23. 1 признак подобия треугольников Теорема: если два угла одного треугольника соответственно равны двум углам другого, то
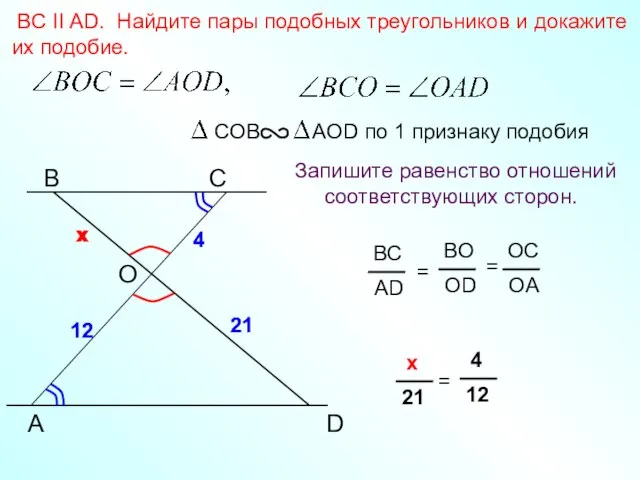
- 24. A B С BC II AD. Найдите пары подобных треугольников и докажите их подобие. Запишите равенство
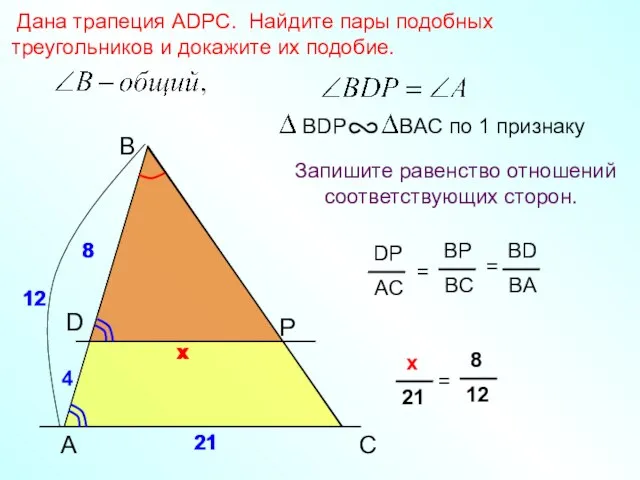
- 25. A B P Дана трапеция АDPC. Найдите пары подобных треугольников и докажите их подобие. Запишите равенство
- 27. Скачать презентацию




 Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции и их свойства Понятие вектора. Длина вектора. Коллинеарные векторы (1)
Понятие вектора. Длина вектора. Коллинеарные векторы (1) Смежные углы
Смежные углы Тренажёр по теме Сложение и вычитание десятичных дробей
Тренажёр по теме Сложение и вычитание десятичных дробей Презентация на тему Уравнения
Презентация на тему Уравнения  Система управління технологічного процесу приготування розчинів для піроксилінових порохів
Система управління технологічного процесу приготування розчинів для піроксилінових порохів Нуль без палочки. Математический турнир
Нуль без палочки. Математический турнир Симметрия. Симметричные объекты. Платоновы тела
Симметрия. Симметричные объекты. Платоновы тела Математика
Математика Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ  Путешествие в страну Геометрию
Путешествие в страну Геометрию История числа Пи
История числа Пи Решение задач Параллельные прямые
Решение задач Параллельные прямые Квадратный корень из степени
Квадратный корень из степени Площадь поверхности цилиндра
Площадь поверхности цилиндра Стереометрия. Подготовка к ЕГЭ, задание В11
Стереометрия. Подготовка к ЕГЭ, задание В11 Тригонометрические уравнения. Найди пару
Тригонометрические уравнения. Найди пару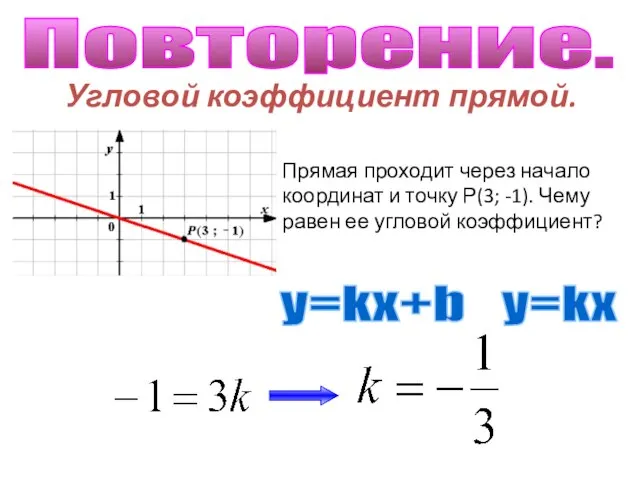 Угловой коэффициент прямой.
Угловой коэффициент прямой. Решение неравенств. 8 класс
Решение неравенств. 8 класс Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс)
Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс) Возрастание и убывание функции
Возрастание и убывание функции Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии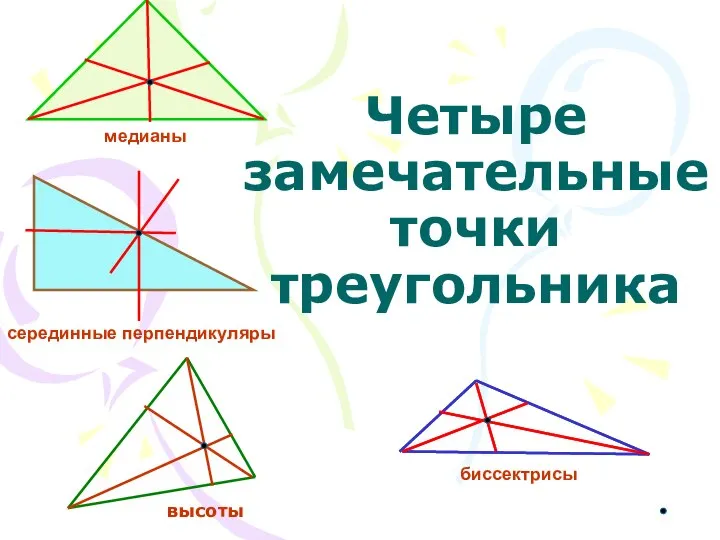 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Презентация на тему Угол между прямыми
Презентация на тему Угол между прямыми  Прикидка результата. 5 класс
Прикидка результата. 5 класс urok_1_10_klass_geom
urok_1_10_klass_geom Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Смысл умножения. Тренажер
Смысл умножения. Тренажер