Содержание
- 2. Цели и задачи Цель работы – изучение возможности параллельной реализация алгоритма Хаффмана, основанной на расширении операций
- 3. Алгоритм построения оптимального кода Хаффмана Символы входного алфавита образуют список из N свободных узлов. Вес узла
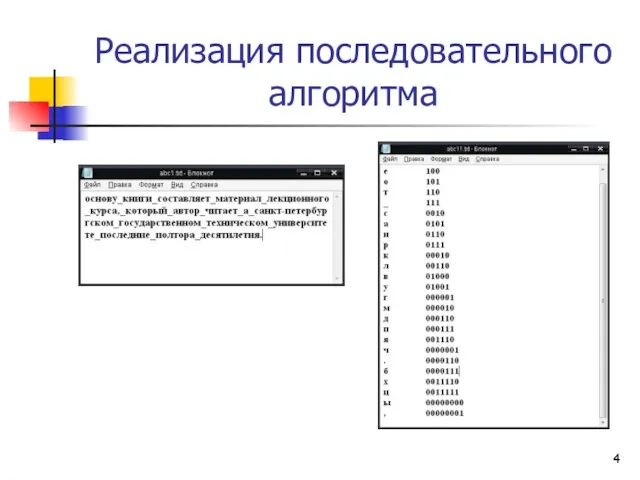
- 4. Реализация последовательного алгоритма
- 5. Оценка сложности последовательного алгоритма Пусть M – число символов в сообщении, кодируемых по Хаффману и принадлежащих
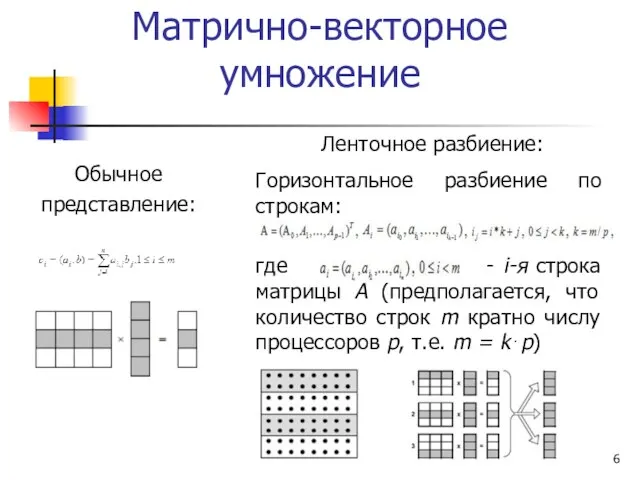
- 6. Матрично-векторное умножение Обычное представление: Ленточное разбиение: Горизонтальное разбиение по строкам: где - i-я строка матрицы A
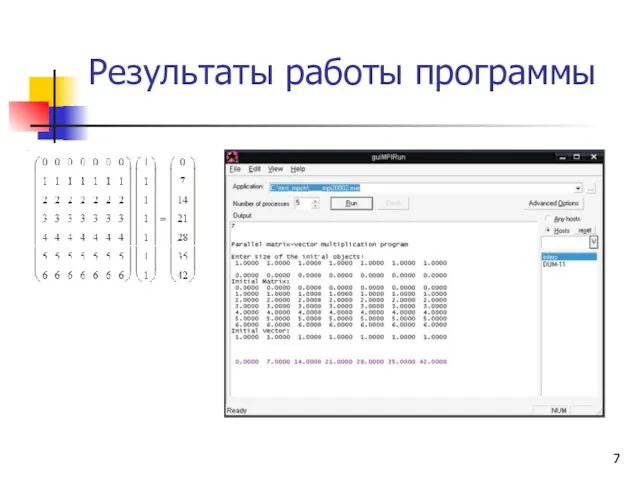
- 7. Результаты работы программы
- 8. Использование матричных операций при построении дерева алгоритма Хаффмана Алгоритм: Определить частоты встречаемости символов в сообщении, составляющих
- 9. Рассмотрим множество, состоящее из элементов 0,1, . Пусть T – множество, которому принадлежат элементы матрицы, и
- 10. Определение частот встречаемости символов в сообщении Представим исходное сообщение, символы которого принадлежат множеству входного алфавита ,
- 11. Использование матричных операций при построении дерева алгоритма Хаффмана
- 12. Упорядочивание узлов дерева Рассмотрим возможность использования введенной операции матричного умножения для упорядочения элементов, составляющих вектор исходных
- 13. Добавление нового узла Для выбора двух минимальных узлов и добавления соответствующего им нового узла–родителя преобразуем вектор
- 14. Формирование кодовых разрядов При добавлении очередной -ой вершины разобьем сформированный вектор на два: вектор , соответствующий
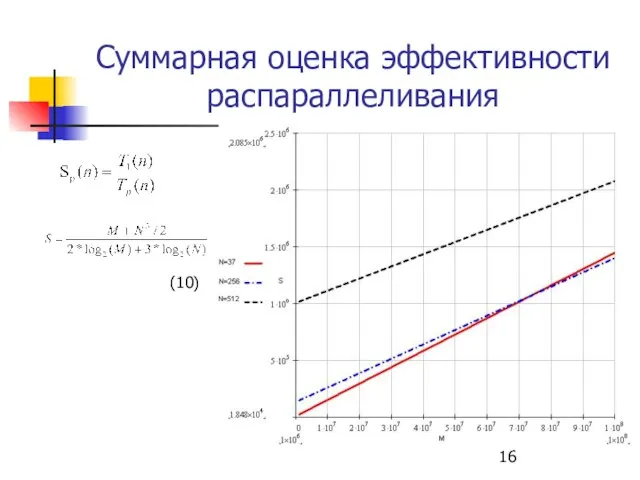
- 15. Суммарная оценка эффективности распараллеливания Определение частот встречаемости символов в сообщении (общее число сложений ): Упорядочение узлов
- 16. Суммарная оценка эффективности распараллеливания (10)
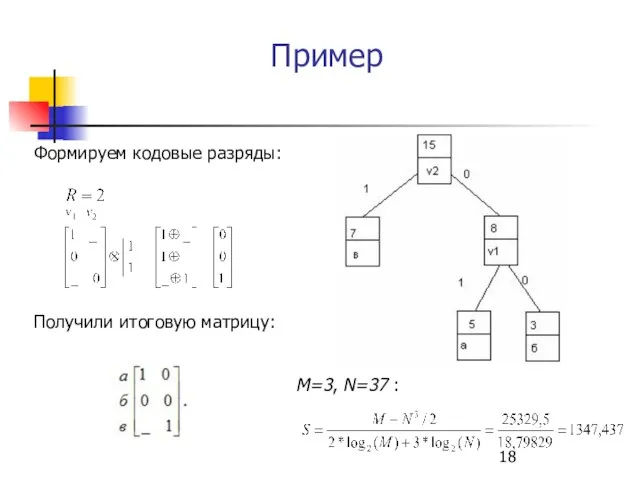
- 17. Пример Пусть задано следующее множество элементов входного алфавита (N=3) и соответствующие им веса: а–5, б–3, в–7.
- 18. Пример Формируем кодовые разряды: Получили итоговую матрицу: M=3, N=37 :
- 20. Скачать презентацию











 Признаки равенства треугольников
Признаки равенства треугольников Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Параллельность прямых и плоскостей (10 класс)
Параллельность прямых и плоскостей (10 класс) Умножение обыкновенных дробей
Умножение обыкновенных дробей TA&Ml_ukr_1
TA&Ml_ukr_1 Инженерно-вычислительные технологии
Инженерно-вычислительные технологии Применение производной к исследованию функции
Применение производной к исследованию функции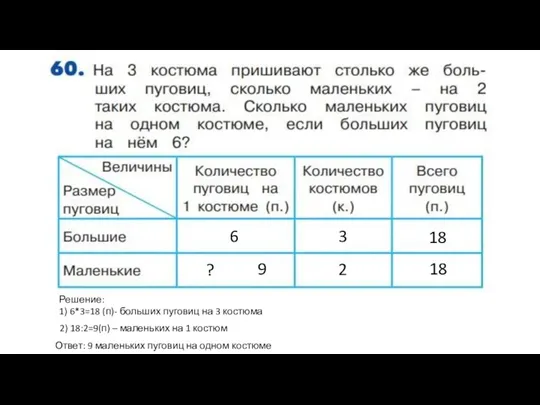 Задача о костюмах
Задача о костюмах Нахождение неизвестного вычитаемого
Нахождение неизвестного вычитаемого Дискретные случайные величины
Дискретные случайные величины Задание В11, открытого банка ЕГЭ по математике (часть 1)
Задание В11, открытого банка ЕГЭ по математике (часть 1) Критерий линейной корреляции Пирсона
Критерий линейной корреляции Пирсона Построение сечений
Построение сечений Логарифмические уравнения и методы их решения
Логарифмические уравнения и методы их решения Решение уравнений сводящихся к линейным
Решение уравнений сводящихся к линейным Золотое сечение в архитектуре, скульптуре, живописи
Золотое сечение в архитектуре, скульптуре, живописи Задачи на построение
Задачи на построение Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже
Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже Презентация на тему Сложение и вычитание чисел 5,6,7,8,9 (1 класс)
Презентация на тему Сложение и вычитание чисел 5,6,7,8,9 (1 класс)  Равносильные уравнения и неравенства
Равносильные уравнения и неравенства Компланарные векторы
Компланарные векторы Цветочное настроение (порядковый счет)
Цветочное настроение (порядковый счет) Венегрет. Урок
Венегрет. Урок Презентация по математике "Портреты учёных математиков" -
Презентация по математике "Портреты учёных математиков" -  График функций. Домашняя работа по алгебре
График функций. Домашняя работа по алгебре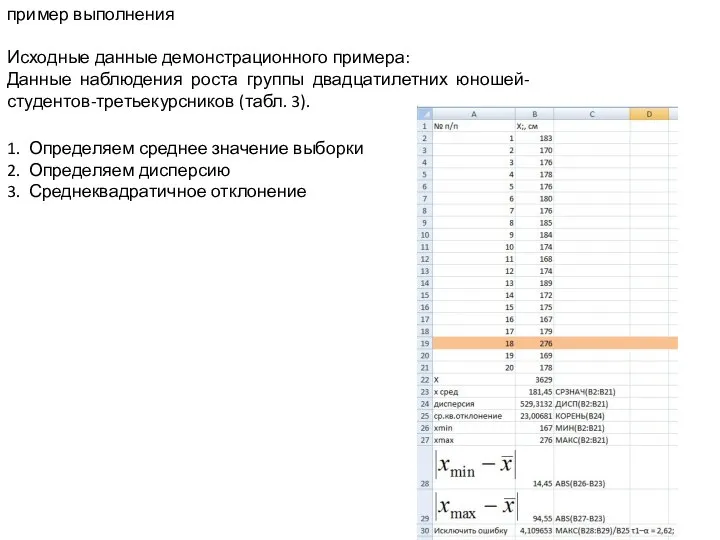 Данные наблюдения роста группы двадцатилетних юношей студентов
Данные наблюдения роста группы двадцатилетних юношей студентов Ломаная линия
Ломаная линия Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс